数值算法对比与应用：欧拉、拉格朗日与SPH

2023-06-18 理论教育版权反馈

【摘要】：图2.3朗格朗日网格与欧拉网格对比欧拉算法也有其不足，体现为单个循环计算时间长、材料边界不清晰、网格区域过大、冲击波耗散大、强度模拟不精确等。图2.4欧拉-拉格朗日耦合算法模型4.SPH算法SPH算法，即光滑粒子流体动力学数值算法，为固体材料大变形，尤其是存在破坏、断裂等极大变形的非线性动力学行为数值模拟提供了新的手段。

1.拉格朗日算法

拉格朗日算法又称为随体法，该方法以物质坐标为基础，在流体运动过程中，追踪流体中各质点，记录质点在运动过程中的各个物理量（如压力P、密度ρ、温度T、流动速度u等）随时间变化的规律。拉格朗日算法最主要的特点是将材料附着在网格上，网格与网格内材料为一体，材料不会在网格与网格之间发生流动，如图2.1所示。有限元节点即物质点，受外界作用力后，材料连同网格一起移动和变形，质点坐标随材料移动。采用该方法时，结构形状的变化和有限单元网格的变化完全一致。

pagenumber_ebook=72,pagenumber_book=55

图2.1　拉格朗日网格变形示意

拉格朗日算法在计算时间、材料边界处理和动态力学性质模拟等方面具有两方面显著优势：一是由于网格与材料一起变形，拉格朗日算法易于确定时间历程，可非常精确地描述材料与结构边界运动状态及内部应力应变状态，对模拟固体材料在小变形时的动态行为具有一定优势；二是拉格朗日算法具有单个循环计算时间短、编码简单、材料强度模拟较好、冲击波耗散小的特点。

但基于拉格朗日算法的网格也有一些固有缺点，如网格扭曲严重时会导致计算误差增加、时间步长逐步减小、滑移接触面逻辑关系定义复杂。尤其是当用拉格朗日算法处理大变形问题时，网格缠结会导致计算效率下降，甚至使计算无法执行，在这种情况下则需要重新划分网格。

2.欧拉算法

在欧拉算法中，一个网格单元中可以有不同物质，不同材料在空间网格中可实现物质输送。因此，对于可能产生严重网格扭曲或相互分离材料发生混合的问题，需使用欧拉算法。欧拉算法中，计算网格固定于空间中，不能随物体运动，而材料可在网格中自由流动，如图2.2所示，因此不存在网格畸变问题。各单元体积在计算过程中保持不变，各时刻的速度、压力、密度和温度等物理量均在空间点上进行计算，而非如拉格朗日算法在物质点上计算，因此质量、动量和能量等物理量将跨越单元边界在单元间输运，各单元的质量、动量和能量等不断发生变化。欧拉算法常用于模拟流体、气体及大变形问题。

pagenumber_ebook=72,pagenumber_book=55

图2.2　欧拉网格材料流动过程

与拉格朗日算法相比，欧拉算法有以下显著特点：

（1）欧拉算法无网格畸变，无须对网格进行重新划分，无须设置侵蚀，适合处理大变形问题，初始状态支持多材料；

（2）欧拉算法只计算质量、动量和能量等物理量在单元间跨越网格边界的输运量，因此难以准确计算材料界面和自由表面位置，因此欧拉算法边界条件的施加比拉格朗日算法更加困难，且精度更低；

（3）欧拉算法中，网格区域需要足够大，以保证有足够的材料流动区域，因此会存在大量空单元（未被材料占据或材料已经流过的单元），而拉格朗日算法只需对物体进行离散，无空单元，如图2.3所示。

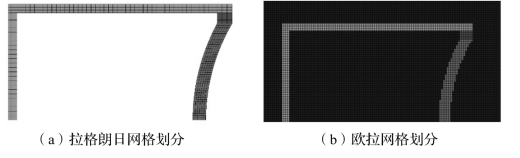
pagenumber_ebook=73,pagenumber_book=56

图2.3　朗格朗日网格与欧拉网格对比

欧拉算法也有其不足，体现为单个循环计算时间长、材料边界不清晰、网格区域过大、冲击波耗散大、强度模拟不精确等。

3.欧拉-拉格朗日耦合算法

欧拉-拉格朗日耦合算法也称为流固耦合算法，可高效、准确地分析流体与固体之间的相互作用。欧拉-拉格朗日耦合算法对爆炸与冲击问题分析优势突出，如计算聚能装药侵彻钢靶，聚能装药采用欧拉网格，靶板采用拉格朗日网格；计算水下爆炸对船体结构破坏效应，水体及炸药采用欧拉算法，船体结构采用拉格朗日算法。

欧拉-拉格朗日耦合算法的特点是，建立几何模型及进行有限元网格划分时，结构与流体的几何区域以及网格可重叠在一起，计算中通过一定约束方法将结构与流体耦合在一起，以实现力学参量的传递，如图2.4所示。

值得注意的是，通过欧拉-拉格朗日耦合算法进行分析时，需要对拉格朗日结构进行约束，并将相关结构参数传递给流体单元。按照算法分类，约束方法包括加速度约束、加速度与速度约束、罚函数约束等。

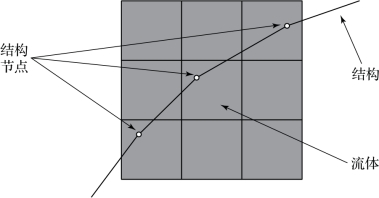
pagenumber_ebook=74,pagenumber_book=57

图2.4　欧拉-拉格朗日耦合算法模型

4.SPH算法

SPH算法，即光滑粒子流体动力学数值算法，为固体材料大变形，尤其是存在破坏、断裂等极大变形的非线性动力学行为数值模拟提供了新的手段。SPH算法最初是针对求解三维开放空间天体物理学问题而提出的，早期应用主要集中于多变性问题研究领域，如磁流体动力学、传热和传质等。随着SPH算法内涵的逐步清晰和理论框架的日趋完善，时至今日，SPH算法已在众多领域得到了广泛应用，如超高速碰撞数值模拟、弹药战斗部终点效应问题数值模拟、爆炸与强载荷冲击问题数值模拟、计算固体力学问题数值模拟等。

从本质而言，SPH算法是一种无网格拉格朗日算法。与有限元法（FEM）和有限差分法（FDM）等基于网格划分技术的传统数值算法相比，SPH算法通过在计算域中填充具有独立材料性质的SPH粒子来替代网格划分，SPH粒子遵守质量、动量和能量守恒方程。其显著特点主要体现在以下几个方面：

（1）SPH算法通过填充无网格SPH粒子的方法对问题计算域进行描述，计算中无须用预先定义好的网格为SPH粒子之间提供相互连接的信息；

（2）SPH算法的无网格SPH粒子不仅可作为插值近似点，还携带有材料性质并发生运动，使SPH粒子更具灵活性，可与拉格朗日算法和谐结合；

（3）SPH算法守恒方程不受SPH粒子分布状态的影响，可自然处理材料在发生极大变形下的非线性动力学问题，体现了良好的自适应性。

正是SPH算法的无网格SPH粒子特性、拉格朗日算法特性及自适应特性三者的结合，使其在固体大变形非线性动力学问题中得到广泛应用。

数值算法对比与应用：欧拉、拉格朗日与SPH

相关推荐