图1.26聚能射流典型破甲过程示意基于上述假设，将坐标原点设置于射流与靶板接触点A，以点A为观察点，射流和靶板材料分别以速度vj-u和速度u运动。以上原因均表明，射流断裂后，侵彻能力将大幅下降。图1.28断裂射流侵彻模型设断裂时射流头部速度为vjB，经过时间t，长度l的断裂射流消耗完毕，侵彻深度为L，速度为vj的点A射流到达孔底D。......
2023-06-18
杆式射流的侵彻理论详解
【摘要】：图1.32杆式射流侵彻理论模型建立过程1.等速等截面杆侵彻模型杆式射流侵彻靶板时，杆式射流沿长度方向可划分为多个连续微元，各微元长度在侵彻前已知，且各微元内直径和速度相同，如图1.33所示。图1.33等速等截面杆微元划分计算时，若忽略“开坑”阶段的能量损失，可认为杆式射流立即达到侵彻速度，杆式射流每一个微元对靶板侵彻，均可看作射流定常侵彻过程。将各段“杆元”侵彻深度之和作为杆式射流总侵彻深度。
杆式射流由特殊形状和厚度的药型罩形成，且与聚能射流、爆炸成型弹丸在形状、速度等方面存在显著差异。杆式射流具有以下3方面特征：一是具有一定的长径比，且长径比介于聚能射流和爆炸成型弹丸之间；二是杆式射流截面直径变化显著，与射流典型线型特征存在较大差别；三是杆式射流存在显著速度梯度，且速度梯度介于爆炸成型弹丸与聚能射流之间。
建立杆式射流侵彻模型时，可将杆式射流划分为多个沿轴线分布的变截面微元，各微元轴向速度按一定规律连续变化，侵彻前各微元截面直径仅与轴向坐标有关。侵彻过程可视作非等速变截面杆侵彻过程，杆式射流可等效为由不同速度不同截面半径离散“杆元”组成的侵彻体，如图1.31所示。
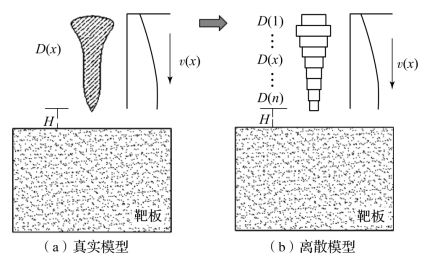
图1.31 杆式射流微元离散
真实模型离散化后，非等速变截面杆模型基本反映了真实杆式射流截面非均匀性、存在速度差的实际特点，如图1.31（b）所示。事实上，直接建立非等速变截面杆侵彻理论模型具有一定困难。但根据杆式射流的特点，非等速变截面杆侵彻理论模型可通过3个步骤建立：首先，建立等速等截面杆侵彻理论模型，如图1.32（a）所示；然后，考虑杆式射流截面直径的变化，建立等速变截面杆侵彻理论模型，如图1.32（b）所示；最后，进一步考虑杆式射流速度的影响，建立非等速变截面杆侵彻理论模型，如图1.32（c）所示。
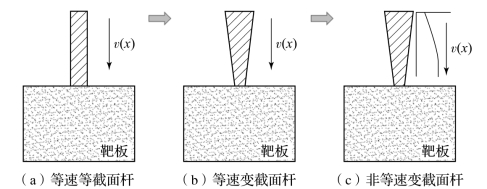
图1.32 杆式射流侵彻理论模型建立过程
1.等速等截面杆侵彻模型
杆式射流侵彻靶板时，杆式射流沿长度方向可划分为多个连续微元，各微元长度在侵彻前已知，且各微元内直径和速度相同，如图1.33所示。
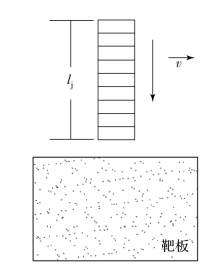
图1.33 等速等截面杆微元划分
计算时，若忽略“开坑”阶段的能量损失，可认为杆式射流立即达到侵彻速度，杆式射流每一个微元对靶板侵彻，均可看作射流定常侵彻过程。
假设某一微元的长度为Li，速度为vi，并假设靶板为均匀各向同性塑性材料。根据射流定常侵彻理论，忽略靶板的强度，则该微元侵彻深度表述为
侵彻速度表述为
若考虑靶板强度对侵彻过程的影响，则修正后的伯努利方程表述为
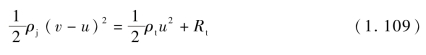
式中，Rt为靶板阻力，则杆式射流第i个微元对靶板侵彻速度为
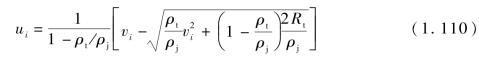
因此，考虑靶板强度的微元侵彻深度可表述为
在侵彻过程中，若杆式射流各微元之间无相互影响，即微元侵彻靶板的先后顺序对侵彻没有影响，则杆式射流对靶板总侵彻深度表述为
2.等速变截面杆侵彻模型
相对于等速等截面杆，等速变截面杆在轴线方向上存在直径变化，即D（x）随x变化，但整个杆条速度仍然一致，如图1.34所示。
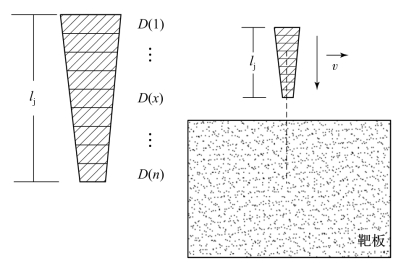
图1.34 等速变截面杆微元划分
建立等速变截面杆侵彻模型，需对等速等截面杆侵彻模型作如下修正：
（1）将变截面杆延长度方向剖分成n段。
（2）将剖分所得“杆元”作为独立侵彻体进行分析，各段“杆元”具有相同的初速和密度，且各段“杆元”长度Li（x）和平均直径Di（x）为变量。“杆元”表征参数为（Li（x），Di（x），ρj，vi），其中Li（x）为“杆元”长度，Di（x）为“杆元”平均直径，取（Di max+Di min）/2，对开孔孔径有直接影响。
（3）将各段“杆元”侵彻深度之和作为杆式射流总侵彻深度。
3.非等速变截面杆侵彻模型
在等速变截面杆侵彻模型的基础上，可进一步建立非等速变截面杆侵彻模型。基于侵蚀杆流体力学不可压缩假设，杆式射流存在轴向速度梯度，在较大炸高条件下，杆式射流在飞行过程中将产生变形，导致其直径变小且长度拉长，进而发生断裂和分离，进而影响“杆元”的侵彻参数。因此必须考虑各“杆元”侵彻前的变形情况，进而对“杆元”参数进行修正，如图1.35所示。
各“杆元”初始参数为（Li（x），Di（x），ρj，vmax，vmin），其中vmax和vmin分别为“杆元”的最大和最小速度。由于炸高H和前导“杆元”侵彻产生的侵彻深度Pjt存在，“杆元”飞行接触靶板前，存在距离Lst=Hs+Pjt。
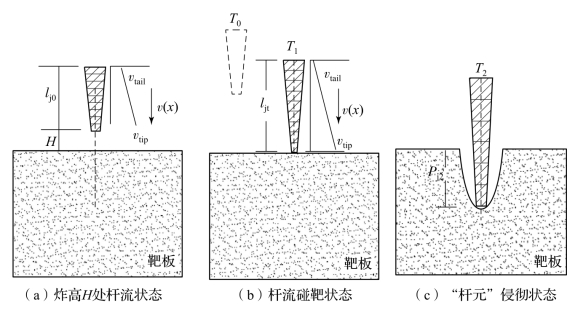
图1.35 非等速变截面杆侵彻靶板理论模型
假设各“杆元”流体不可压缩，且在长度方向存在速度差，导致“杆元”侵彻前会被拉长，拉伸后“杆元”长度为
“杆元”由于拉长导致直径变小，由于体积不变，杆元直径变为
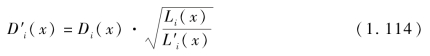
非等速变截面杆侵彻模型及“杆元”变形方程修正时需注意：（1）将变截面杆沿长度方向等分成n段；（2）将等分得到的各段“杆元”作为独立侵彻体进行分析，各段“杆元”密度相同，同时需考虑速度差导致的“杆元”长度及直径变化，速度取“杆元”最大和最小速度的平均值vi=（vi max+vi min）/2，即修正后“杆元”参数为（L′i（x）、D′i（x）、ρj，vi）；（3）以各段“杆元”独立侵彻深度总和作为杆式射流总侵彻深度。
有关活性毁伤增强聚能战斗部技术的文章
- 详细阅读
-
深入探究杆式射流成形理论详细阅读
总的来说，杆式射流成形应遵循以下3方面原则。图1.25药型罩压垮过程2）较小头、尾速度差根据射流形成理论，射流和杵体速度vj、vs分别表述为式中，α和δ分别为药型罩半锥角和偏转角。......
2023-06-18
-
活性聚能侵彻体的侵彻机理详细阅读
图4.20复合结构活性药型罩聚能装药对钢靶毁伤效应图4.21活性聚能战斗部作用钢靶毁伤原理对于所给定的聚能装药结构，炸高对活性聚能侵彻体成形和侵彻效应影响显著。由于反应弛豫时间存在，活性聚能侵彻体发生化学反应之前，才能对目标产生类似惰性侵彻体的侵彻毁伤行为。由图4.23还可得到，活性聚能侵彻体侵彻钢靶的侵彻规律与金属铜射流大致相同，即侵彻深度随着侵彻时间呈指数增长趋势。......
2023-06-18
-
类射流活性聚能侵彻体释能模型探析详细阅读
与此同时，活性聚能侵彻体后部杵体形成，变形过程中温度继续升高，由于未到达激活弛豫时间，未发生反应。图3.2类射流活性聚能侵彻体化学能分布式释放计算模型根据类射流活性聚能侵彻体的形状，其可分为头部、中部及杵体3部分。式即类射流活性聚能侵彻体化学能随时间分布释放模型。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
-
类杆流活性聚能侵彻体释能模型探析详细阅读
图3.5类杆流活性聚能侵彻体化学能分布式释放过程虽然各微元速度梯度较类射流活性聚能侵彻体明显更小，但类杆流活性聚能侵彻体在运动及成形过程中不断拉伸延长，在t2时刻，长度为L2。在继续拉伸过程中，类杆流活性聚能侵彻体逐渐形成，整体密度降低，且由外至内、由头部至尾部，密度均逐渐下降。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
-
侵彻作用模型的探讨与优化详细阅读
跑道由混凝土层、碎石层、土基层构成，活性聚能侵彻体作用跑道时，产生压缩波，形成压缩区。图5.35活性聚能侵彻体侵彻跑道模型微元i开始侵彻靶板时，侵彻深度为Pi-1，则微元i到达目标的时间表述为对于活性聚能侵彻体，由于反应弛豫时间τ的存在，当ti≥τ时，侵彻结束，此时侵彻深度即Pi-1；当ti＜τ时，侵彻继续进行。当考虑反射波的影响时，绝对侵彻速度按式～式计算；当考虑透射波的影响时，绝对侵彻速度按式～式计算。......
2023-06-18
-
侵彻速度对装药损伤断裂的影响详细阅读
图5－22 所示为不同速度下弹体和装药的平均过载变化曲线。图5－23 所示为不同着靶速度下对装药最终裂纹分布的影响，弹体着靶速度为400 m／s 时，装药基本没有出现裂纹损伤区，单元最大裂纹宽度为0.14 mm，说明较低的着靶速度几乎不会使内部装药产生损伤。随着弹体着靶速度的增加，装药裂纹区域扩大，损伤度增加，尾部装药更容易受拉伸波作用产生横向裂纹。着靶速度为700 m／s 和800 m／s 时装药的损伤度分别为1.84%和2.05%。......
2023-06-27
-
深入探析爆炸成型弹丸侵彻原理详细阅读
爆炸成型弹丸是长径比为4～8、速度为1 500～3 000 m/s的恒速杆。爆炸成型弹丸在侵彻过程中会出现变形和侵蚀，且撞击速度较低，因此材料强度对侵彻过程影响较大。爆炸成型弹丸侵彻过程常以长杆侵蚀侵彻公式为基础，本节主要介绍长杆侵蚀侵彻理论模型和Allen-Rogers侵彻模型。第三阶段出现在长杆被完全侵蚀后，称为二次侵彻或残余塑性流动阶段。当ρj=ρt=ρ时，得到相对侵彻深度公式可表述为爆炸成型弹丸侵彻实验结果及模型预测曲线如图1.30所示。......
2023-06-18
相关推荐