研究表明，当半锥角接近75°时，射流和杵体速度几乎相同，如图1.21所示，将形成爆炸成型弹丸。取中间值0.36，根据式和式计算出当药型罩锥角为137°时，射流和杵体合一，形成爆炸成型弹丸。当曲率半径偏离式过多时，则会导致无法形成爆炸成型弹丸。......
2023-06-18
深入探析爆炸成型弹丸侵彻原理
【摘要】：爆炸成型弹丸是长径比为4～8、速度为1 500～3 000 m/s的恒速杆。爆炸成型弹丸在侵彻过程中会出现变形和侵蚀，且撞击速度较低，因此材料强度对侵彻过程影响较大。爆炸成型弹丸侵彻过程常以长杆侵蚀侵彻公式为基础，本节主要介绍长杆侵蚀侵彻理论模型和Allen-Rogers侵彻模型。第三阶段出现在长杆被完全侵蚀后，称为二次侵彻或残余塑性流动阶段。当ρj=ρt=ρ时，得到相对侵彻深度公式可表述为爆炸成型弹丸侵彻实验结果及模型预测曲线如图1.30所示。
爆炸成型弹丸是长径比为4～8、速度为1 500～3 000 m/s的恒速杆。爆炸成型弹丸在侵彻过程中会出现变形和侵蚀，且撞击速度较低，因此材料强度对侵彻过程影响较大。爆炸成型弹丸侵彻过程常以长杆侵蚀侵彻公式为基础，本节主要介绍长杆侵蚀侵彻理论模型和Allen-Rogers侵彻模型。
根据长杆与靶界面上的压力分布，长杆侵彻过程可分为4个阶段，如图1.29所示。第一阶段为“开坑”阶段，撞击产生的冲击波分别向前和向后传入靶板和长杆，导致长杆头部发生大变形。第二阶段为准稳态侵彻阶段，这是大长径比高速杆的主要侵彻模式。第三阶段出现在长杆被完全侵蚀后，称为二次侵彻或残余塑性流动阶段。“二次侵彻”是指在一定条件下，杆进行反向侵彻，使侵彻深度继续增加；“残余塑性流动”是在长杆全部侵蚀后，靶板的动量仍足以克服靶板强度，成坑继续增长，侵彻深度继续增加。第四阶段为侵彻过程结束后，靶板的弹性恢复阶段，该阶段基本不影响长杆侵彻深度。
图1.29 长杆侵彻过程阶段划分
在长杆侵彻过程中，假设靶界面中心线两侧压力相等，依据修正后的伯努利方程，可以得出
假设杆中不存在速度梯度，设式（1.96）中断裂系数g=1.0。若长杆由非常软的材料制成，式中σ只受靶板强度影响，则可忽略长杆强度的影响。通过求解式（1.96），可得到侵彻速度u的表达式为
式中，
式中，γ为靶板和长杆密度比的平方根。
对式（1.97）进行积分，相对侵彻深度可表述为
当撞击速度很大时，可以忽略Q，此时相对侵彻深度可表述为
式（1.100）即理想射流侵彻深度公式。
当ρj=ρt=ρ时，得到
相对侵彻深度公式可表述为
爆炸成型弹丸侵彻实验结果及模型预测曲线如图1.30所示。从图中可以看出，除了金杆在高速撞击条件下有较大的误差外，其他实验结果都符合流体力学模型；在高速撞击下，靶板强度对侵彻深度影响不大，通过模型预测的P/L与流体动力学极限（ρj/ρt）0.5趋近。
图1.30 实验数据及模型预测曲线对比
通过实验结果可知，对于给定杆，存在一个临界侵彻速度vc，当撞击速度大于vc时，杆才开始侵彻。将u=0代入式（1.96），得到临界侵彻速度为
式中，σt为靶板侵彻阻抗。
当动态撞击压力和靶板侵彻阻抗相等时，侵彻速度即临界侵彻速度。
根据临界侵彻速度，对同等密度靶板的相对侵彻深度公式可改写为
由式（1.104）可知，一旦临界侵彻速度确定，就可给出相对侵彻深度（P/L）随相对速度（Z=v0/vc）变化关系。
研究表明，高速金杆侵彻深度相对较大，进一步分析可知，靶板和长杆密度比（ρj/ρt）足够大，且撞击速度大于临界侵彻速度时，反向杆将继续侵彻靶板，即产生二次侵彻现象，导致侵孔深度进一步增大。
为进一步分析二次侵彻效应，人们通过X光实验研究了铝杆和钢杆作用不同靶板的侵彻过程，实验中长杆的长径比L/D为0.17～25。实验结果表明，“二次侵彻”阶段从杆被完全侵蚀开始，直至靶后冲击波能量密度不足以克服靶板阻抗为止。实验中还观察到主侵彻和二次侵彻同时存在。但当撞击速度低于2 km/s时，长杆未完全发生侵蚀，表明长杆后半部分在侵彻过程中不断减速。以上分析表明，撞击速度较低时，稳态侵彻过程无法完成。
根据实验结果，可建立侵彻深度半经验模型。主侵彻阶段基于稳态流体动力学过程分析，持续至L/D=1，而长杆剩余部分会额外增加侵彻深度。
增加的侵彻深度取决于剩余长杆速度和靶板强度，靶板强度可通过硬度值Bh表示，则总侵彻深度半经验公式可表述为
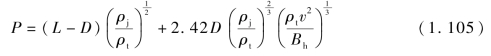
二次侵彻项可表述为
综上所述，爆炸成型弹丸侵彻靶板总侵深可分为两部分，一是弹丸主侵彻深度，二是剩余弹丸（L/D=1）侵彻深度。其中，剩余长杆造成的额外侵彻深度指长杆最后一部分继续侵彻直至杆长减小到零所造成的侵彻深度。
有关活性毁伤增强聚能战斗部技术的文章
- 详细阅读
-
活性聚能侵彻体的侵彻机理详细阅读
图4.20复合结构活性药型罩聚能装药对钢靶毁伤效应图4.21活性聚能战斗部作用钢靶毁伤原理对于所给定的聚能装药结构，炸高对活性聚能侵彻体成形和侵彻效应影响显著。由于反应弛豫时间存在，活性聚能侵彻体发生化学反应之前，才能对目标产生类似惰性侵彻体的侵彻毁伤行为。由图4.23还可得到，活性聚能侵彻体侵彻钢靶的侵彻规律与金属铜射流大致相同，即侵彻深度随着侵彻时间呈指数增长趋势。......
2023-06-18
-
类弹丸聚能侵彻体释能模型的活性分析详细阅读
类弹丸活性聚能侵彻体化学能分布式释放过程如图3.3所示。爆轰波完全扫过活性药型罩后，罩体内压力及温度进一步升高，活性药型罩顶部发生明显形变，在轴线处发生翻转，形成类弹丸活性聚能侵彻体头部。基于以上假设，以侵彻体尾部端面中点为原点，建立二维平面物质坐标系，类弹丸活性聚能侵彻体化学能分布式释放计算模型如图3.4所示。在继续成形过程中，侵彻体中部及尾裙部分温度逐渐升高，相继发生激活。......
2023-06-18
-
类射流活性聚能侵彻体释能模型探析详细阅读
与此同时，活性聚能侵彻体后部杵体形成，变形过程中温度继续升高，由于未到达激活弛豫时间，未发生反应。图3.2类射流活性聚能侵彻体化学能分布式释放计算模型根据类射流活性聚能侵彻体的形状，其可分为头部、中部及杵体3部分。式即类射流活性聚能侵彻体化学能随时间分布释放模型。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
-
类杆流活性聚能侵彻体释能模型探析详细阅读
图3.5类杆流活性聚能侵彻体化学能分布式释放过程虽然各微元速度梯度较类射流活性聚能侵彻体明显更小，但类杆流活性聚能侵彻体在运动及成形过程中不断拉伸延长，在t2时刻，长度为L2。在继续拉伸过程中，类杆流活性聚能侵彻体逐渐形成，整体密度降低，且由外至内、由头部至尾部，密度均逐渐下降。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
-
深入探析间歇运动机构的工作原理详细阅读
任务要求掌握典型间歇机构及工作原理。其工作过程与棘轮机构相似，主动棘爪2靠它与棘轮3之间产生的摩擦力来驱使棘轮作间歇运动。图2.54槽轮1—拨盘；2—槽轮图2.55内槽轮机构图2.56六角车床刀架的转位槽轮机构2.3.3不完全齿轮机构不完全齿轮机构是由渐开线齿轮机构演变而成的间歇运动机构。它属于间歇运动机构。......
2023-06-30
-
聚能射流侵彻的理论探究详细阅读
图1.26聚能射流典型破甲过程示意基于上述假设，将坐标原点设置于射流与靶板接触点A，以点A为观察点，射流和靶板材料分别以速度vj-u和速度u运动。以上原因均表明，射流断裂后，侵彻能力将大幅下降。图1.28断裂射流侵彻模型设断裂时射流头部速度为vjB，经过时间t，长度l的断裂射流消耗完毕，侵彻深度为L，速度为vj的点A射流到达孔底D。......
2023-06-18
-
杆式射流的侵彻理论详解详细阅读
图1.32杆式射流侵彻理论模型建立过程1.等速等截面杆侵彻模型杆式射流侵彻靶板时，杆式射流沿长度方向可划分为多个连续微元，各微元长度在侵彻前已知，且各微元内直径和速度相同，如图1.33所示。图1.33等速等截面杆微元划分计算时，若忽略“开坑”阶段的能量损失，可认为杆式射流立即达到侵彻速度，杆式射流每一个微元对靶板侵彻，均可看作射流定常侵彻过程。将各段“杆元”侵彻深度之和作为杆式射流总侵彻深度。......
2023-06-18
相关推荐