与此同时，活性聚能侵彻体后部杵体形成，变形过程中温度继续升高，由于未到达激活弛豫时间，未发生反应。图3.2类射流活性聚能侵彻体化学能分布式释放计算模型根据类射流活性聚能侵彻体的形状，其可分为头部、中部及杵体3部分。式即类射流活性聚能侵彻体化学能随时间分布释放模型。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
聚能射流侵彻的理论探究
【摘要】：图1.26聚能射流典型破甲过程示意基于上述假设，将坐标原点设置于射流与靶板接触点A，以点A为观察点，射流和靶板材料分别以速度vj-u和速度u运动。以上原因均表明，射流断裂后，侵彻能力将大幅下降。图1.28断裂射流侵彻模型设断裂时射流头部速度为vjB，经过时间t，长度l的断裂射流消耗完毕，侵彻深度为L，速度为vj的点A射流到达孔底D。
1.定常流体力学侵彻理论
聚能射流典型破甲过程示意如图1.26所示，射流速度为vj，破甲速度为u。假定射流与靶板作用过程是稳态的，可把破甲过程当作理想不可压缩流体运动过程来处理。分析过程中作如下假设：
（1）忽略靶板和射流强度及可压缩性；
（2）假定分析中射流直径、速度vj及破甲速度u均不变。
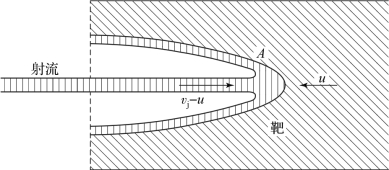
图1.26 聚能射流典型破甲过程示意
基于上述假设，将坐标原点设置于射流与靶板接触点A，以点A为观察点，射流和靶板材料分别以速度vj-u和速度u运动。
假设恒速射流长度为l，总破甲时间为t，则
破甲深度为
在侵彻时间t内，破甲过程为定常理想不可压缩流体运动过程。应用伯努利方程，在点A左侧，取远离A点的一点和点A，可得
式中，
为远离点A处射流静压力；（Pj）A为点A左侧射流静压力，该处速度u为0。
在点A右侧，取远离点A的一点和点A，可得
式中，
为远离点A处靶板静压力；（Pt）A为点A右侧靶板静压力，该处速度u为0。
点A两侧压力在点A相等，有
（Pt）A=（Pj）A
由此可得
式中，ρj和ρt分别为射流和靶板密度。
忽略
和
式（1.66）可写为
代入式（1.64）和式（1.65），消去t得
根据式（1.68）可知，破甲深度与射流长度成正比，适当增加炸高，射流长度l增加，在射流不断裂和分散的情况下，破甲深度增加；破甲深度与射流和靶板密度之比的平方根成正比，射流密度越大，侵彻深度越大。
式（1.68）表明，射流破甲深度与靶板强度、射流速度均无关，仅取决于射流长度和射流与靶板密度之比。分析中假设靶板是理想流体，不考虑其强度，射流速度较低时也能在靶板上形成穿孔，这显然与实际不符。但由于射流头部速度很高，靶板强度的影响可以忽略。然而，定常流体力学侵彻理论未考虑射流速度梯度，因此还需对上述理论进行修正。
2.准定常流体力学侵彻理论
事实上，在破甲过程中，射流头部速度高于尾部速度，沿射流长度方向存在速度分布，导致射流速度和直径不断变化，这和上述假定的恒速射流不同，在准定常流体力学侵彻理论中，不能直接应用伯努利方程。然而，针对某小段射流微元，可近似认为速度和直径不变，则亦可应用伯努利方程。
基于Allison和Vitali的假设，射流是从某固定原点发出，该固定原点为虚拟原点，如图1.27所示。在射流侵彻深度-时间坐标系中，y轴为轴向距离，且以药型罩锥底为0点；t轴为时间，以爆轰波到达药柱底部为0点；点A为虚拟原点。假设射流速度沿长度方向线性分布，在t-y坐标系中，射流是从点A发出的一族直线，各直线斜率对应该射流微元速度，H为炸高。在点B时射流头部与靶板相遇，开始侵彻，BC线描述侵深随时间变化的关系，曲线上各点斜率对应该点破甲速度u。以点C为例，侵彻深度为L，点C切线斜率为u，AC线斜率即射流速度vj，到点D时侵彻停止，最大侵彻深度为LM。
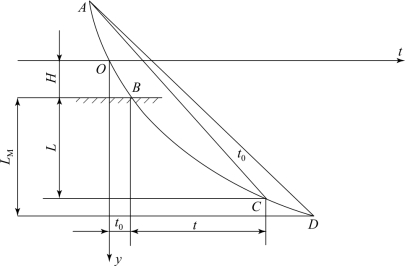
图1.27 聚能射流侵彻模型
对某一点C，侵彻深度为L，侵彻时间为t，则
对t微分，因H-b为常数，且dL/dt=u，则有
积分得
式中，t0是射流头部到达靶板的时间。将t代入式（1.69），可得
对于理想不可压缩流体，vj和u的关系由式（1.67）给出，可得
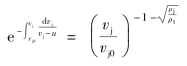
代入式（1.73）得
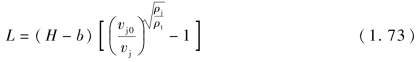
这就是准定常理想不可压缩流体的侵彻公式。
由式（1.74）也可得出L和t的关系。将式（1.67）代入式（1.72），即
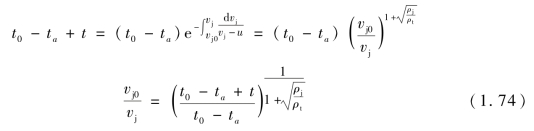
代入式（1.73），得
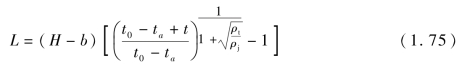
在式（1.74）和式（1.75）中，已考虑射流速度分布，与实际情况更加接近，但仍未考虑射流断裂和靶板强度的影响，因此还需进一步修正。
3.考虑靶板强度的侵彻理论
事实上，射流侵彻过程显著受靶板强度影响，尤其是当射流速度较低时，更不能忽略靶板强度的影响。考虑靶板强度时，侵彻深度可由式（1.66）表述为
在理想不可压缩流体理论中，
取值为0。通过静压力描述材料强度，令
则式（1.66）可表述为
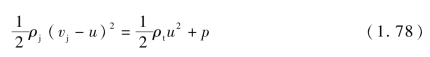
由式（1.78），可求得
将其代入式（1.75），即可得到考虑靶板强度的侵彻公式。由式（1.78）有
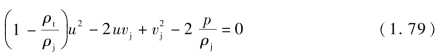
当侵彻速度u=0时，侵彻过程停止，此时对应的射流速度即临界速度vjc，当射流速度低于临界速度时则无法侵彻。将u=0代入式（1.79），可得
再将式（1.80）代入式（1.79），得
令γ=ρt/ρj，则可得
令
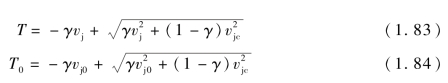
则式（1.82）的解为
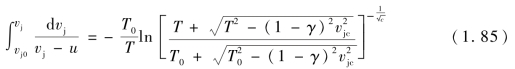
代入式（1.73），得
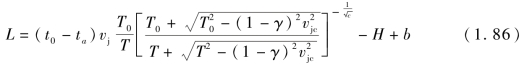
式（1.86）即考虑靶板强度的准定常不可压缩流体方程。式中vjc与射流材料、射流状态及靶板材料有关。当vjc=0时，上式即理想流体侵彻公式。
4.断裂射流侵彻流体力学理论
实际上，当射流在空气中拉伸至一定长度后，会出现颈缩，甚至断裂成小段。射流断裂后，各小段射流长度不再变化，继续运动时，断裂小段射流之间的距离会逐渐增大。当各段射流侵彻时，由于其时间间隔过长，前一段射流侵彻产生的应力状态消失后，后续射流段侵彻时需重新“开坑”，因此需要额外消耗能量。除此之外，断裂射流在空气中运动时会发生翻转，逐渐偏离轴线。以上原因均表明，射流断裂后，侵彻能力将大幅下降。
然而，在断裂初始阶段，各段射流间距离较小，前段射流穿孔产生的应力状态未完全卸载，射流段也未发生明显翻转及偏离，与连续射流相比，仅有射流不伸长这一点差异。同时需要注意的是，侵彻靶板时，断裂射流的速度相当低，不可忽略靶板强度的影响，因此需推导考虑靶板强度的断裂射流侵彻理论。
在tB时刻以后，假设某段射流断裂成若干不再伸长的小射流段，tB为断裂时间，此时侵彻深度为LB，如图1.28所示。此时刻之后，射流总长度不变，且与断裂段数无关。忽略各段射流侵彻时重新“开坑”和翻转的影响，断裂后各段射流速度分布仍遵循断裂前线性分布规律。射流AB可看作未发生断裂，连续侵彻深度为L，经历时间为te。经过间隙时间tf后，后续射流头部A到达孔底D，继续侵彻。无论射流AB断裂成多少段，最后总是到达点D。当射流段数无限多时，射流AB的L-t曲线即可通过光滑曲线BD表示。
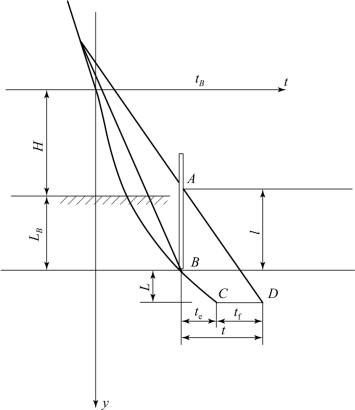
图1.28 断裂射流侵彻模型
设断裂时射流头部速度为vjB，经过时间t，长度l的断裂射流消耗完毕，侵彻深度为L，速度为vj的点A射流到达孔底D。在时刻tB，有
在时刻tB+t，有
联立两式，可得
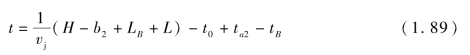
计算断裂射流侵彻深度时，假设图1.28中射流AB在tB以后同时断裂，总侵彻深度相当于长度不再增加的连续射流AB的侵彻深度，而K为tB时刻射流速度梯度。因此有
整理上式，可得
在考虑强度的情况下，通过式（1.80），vj和u的关系可表述为
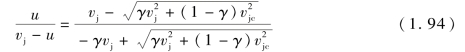
化简式（1.92），代入式（1.91），积分可得
式（1.89）和式（1.95）即考虑靶板强度的条件下，断裂射流的准定常不可压缩流体侵彻公式。
有关活性毁伤增强聚能战斗部技术的文章
- 详细阅读
-
聚能射流成形的理论探究详细阅读
图1.13射流成形定常流动模型建立射流成形的定常流体力学理论，所作假设如下：爆轰波到达药型罩表面，微元以大小和方向不变的压合速度运动；各微元速度v0及变形角δ相等；变形过程中罩长度不变，即AC=BC。......
2023-06-18
-
活性聚能侵彻体的侵彻机理详细阅读
图4.20复合结构活性药型罩聚能装药对钢靶毁伤效应图4.21活性聚能战斗部作用钢靶毁伤原理对于所给定的聚能装药结构，炸高对活性聚能侵彻体成形和侵彻效应影响显著。由于反应弛豫时间存在，活性聚能侵彻体发生化学反应之前，才能对目标产生类似惰性侵彻体的侵彻毁伤行为。由图4.23还可得到，活性聚能侵彻体侵彻钢靶的侵彻规律与金属铜射流大致相同，即侵彻深度随着侵彻时间呈指数增长趋势。......
2023-06-18
-
杆式射流的侵彻理论详解详细阅读
图1.32杆式射流侵彻理论模型建立过程1.等速等截面杆侵彻模型杆式射流侵彻靶板时，杆式射流沿长度方向可划分为多个连续微元，各微元长度在侵彻前已知，且各微元内直径和速度相同，如图1.33所示。图1.33等速等截面杆微元划分计算时，若忽略“开坑”阶段的能量损失，可认为杆式射流立即达到侵彻速度，杆式射流每一个微元对靶板侵彻，均可看作射流定常侵彻过程。将各段“杆元”侵彻深度之和作为杆式射流总侵彻深度。......
2023-06-18
-
类弹丸聚能侵彻体释能模型的活性分析详细阅读
类弹丸活性聚能侵彻体化学能分布式释放过程如图3.3所示。爆轰波完全扫过活性药型罩后，罩体内压力及温度进一步升高，活性药型罩顶部发生明显形变，在轴线处发生翻转，形成类弹丸活性聚能侵彻体头部。基于以上假设，以侵彻体尾部端面中点为原点，建立二维平面物质坐标系，类弹丸活性聚能侵彻体化学能分布式释放计算模型如图3.4所示。在继续成形过程中，侵彻体中部及尾裙部分温度逐渐升高，相继发生激活。......
2023-06-18
-
活性聚能侵彻体成形行为建模方法详细阅读
表2.1活性聚能装药结构材料模型氟聚物基活性材料是一种特殊的含能材料，具有通常条件下惰性钝感、高应变率加载下发生非自持化学反应的特征。表2.2活性药型罩与45钢材料主要参数8701炸药是一种常用混合炸药，爆轰产物通过JWL状态方程描述，8701炸药材料主要参数列于表2.3，空气材料主要参数列于表2.4。表2.38701炸药材料主要参数表2.4空气材料主要参数活性聚能装药数值模型如图2.6所示。......
2023-06-18
-
类杆流活性聚能侵彻体释能模型探析详细阅读
图3.5类杆流活性聚能侵彻体化学能分布式释放过程虽然各微元速度梯度较类射流活性聚能侵彻体明显更小，但类杆流活性聚能侵彻体在运动及成形过程中不断拉伸延长，在t2时刻，长度为L2。在继续拉伸过程中，类杆流活性聚能侵彻体逐渐形成，整体密度降低，且由外至内、由头部至尾部，密度均逐渐下降。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
-
深入探究杆式射流成形理论详细阅读
总的来说，杆式射流成形应遵循以下3方面原则。图1.25药型罩压垮过程2）较小头、尾速度差根据射流形成理论，射流和杵体速度vj、vs分别表述为式中，α和δ分别为药型罩半锥角和偏转角。......
2023-06-18
相关推荐