首页理论教育深入探究杆式射流成形理论

深入探究杆式射流成形理论

2023-06-18 理论教育版权反馈

【摘要】：总的来说，杆式射流成形应遵循以下3方面原则。图1.25药型罩压垮过程2）较小头、尾速度差根据射流形成理论，射流和杵体速度vj、vs分别表述为式中，α和δ分别为药型罩半锥角和偏转角。

杆式射流是由大锥角或扁球壳药型罩在装药爆炸驱动下，向轴心收拢，并在轴心处发生碰撞，形成的速度高、直径大、速度梯度小的射流。与普通射流相比，杆式射流具有对炸高不敏感、药型罩利用率高、后效大的特点；与爆炸成型弹丸相比，杆式射流的飞行速度更高、聚能侵彻体长度更长、侵彻能力更强。

1.杆式射流成形参数

杆式射流本质上也是射流，它只是常规射流的杵体质量减小，头、尾速度差降低，射流整体速度提高的产物，因此可用射流理论进行分析。

一般杆式射流聚能装药由药型罩、壳体、主装药、VESF板、辅助装药等组成，如图1.23所示。VESF板是形状特殊的金属或塑料板，雷管起爆后，辅助装药驱动VESF板撞击、起爆主装药，通过调节VESF板的形状、材料及其与主装药的距离，调整主装药中形成的爆轰波形，可实现杆式射流成形。

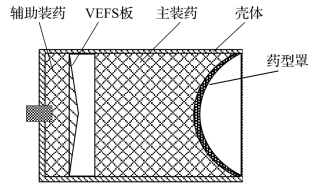
pagenumber_ebook=45,pagenumber_book=28

图1.23　杆式射流聚能装药基本结构

对于带VESF板的聚能装药，装药起爆后，爆轰波绕过VESF板向药型罩传播，在此过程中爆轰波在轴线处发生碰撞，根据碰撞时爆轰波之间夹角的不同可以分为正规斜碰撞和马赫碰撞，爆轰波传播过程如图1.24所示。

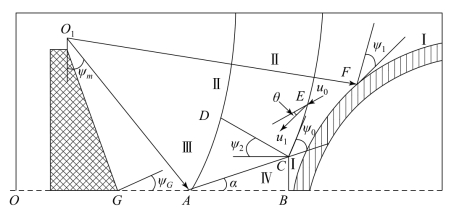
pagenumber_ebook=45,pagenumber_book=28

图1.24　爆轰波传播过程

当装药在点O起爆后，爆轰波绕过隔板到达点O1，此时，可看作以点O1为圆心形成环形起爆。爆轰波在炸药中传播，首先在轴线上点G发生碰撞，入射角为爆轰波阵面与轴线的夹角ψG。碰撞点沿轴线从点G移动到点A的过程中，入射角逐渐增大，F.Muller通过实验发现，当入射角增大到约44.5°时，反射波将与固壁脱离，在固壁附近形成马赫波。图中点A的入射角Ψm=44.5°，入射角达到临界值，点A即正规斜碰撞与马赫碰撞的分界点。

发生马赫反射后，反射波逐渐脱离装药轴线，图中AC代表马赫杆移动方向，三波点C为爆轰波传到点C时入射波波阵面CE、反射波波阵面CD和马赫杆CB的交点。三波点附近流场被CA、CB、CD、CE分为4个区域，马赫杆运动方向与轴线的夹角为α。从图中可以看出，三波点处入射角ψ0为入射波阵面CE和轴线的夹角与α的差，α可以根据下式得到：

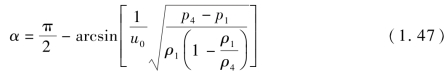
pagenumber_ebook=45,pagenumber_book=28

式中，u0=Dc/sinψ0，其中Dc为炸药爆速；p1、p4分别为Ⅰ区和Ⅳ区压力；ρ1、ρ4分别为Ⅰ区和Ⅳ区密度：

pagenumber_ebook=46,pagenumber_book=29

式中，pCJ为炸药CJ压力；η为过度压缩系数，η=1.1。

马赫杆传播过程中，入射角Ψ0逐渐增大，相应压力逐渐降低，可以通过马赫杆两侧爆轰产物流动基本方程及状态方程求出Ⅳ区的压力p4与ψ0的关系：

pagenumber_ebook=46,pagenumber_book=29

在Ⅲ区，爆轰波正规斜碰撞压力为p3，当爆轰波作用于点F，穿入爆轰波阵面后产物以速度μ1流入Ⅱ区，发生角度为θ的折转。

根据波阵面前、后质量守恒和动量守恒方程，θ可表述为

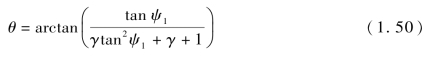
pagenumber_ebook=46,pagenumber_book=29

式中，γ为炸药多方指数，一般取γ=3；ψ1为正规斜碰撞入射角，即爆轰波在点F的切线与药型罩在点F的切线之间的夹角。

当爆轰产物继续运动到反射波阵面，爆轰产物到达Ⅲ区的压力p3即正规斜碰撞后的压力，由反射波阵面处守恒方程及相关几何关系可知

式中，ψ2为反射角。ψ1、ψ2与θ的关系可表示为

pagenumber_ebook=46,pagenumber_book=29

爆轰波对药型罩的作用，包括罩顶马赫压力作用区及罩中部到口部所受正规斜碰撞压力，可根据马赫杆运动与药型罩的几何形状求得。

基于改进的PER理论，对于任意形状药型罩，根据伯努利方程可求得药型罩微元形成的射流速度：

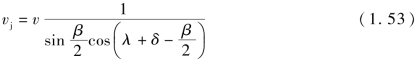
pagenumber_ebook=46,pagenumber_book=29

式中，v为药型罩微元的绝对压垮速度；β为压合角；λ为药型罩切线与轴线的夹角；δ为药型罩微元的偏转角。

绝对压垮速度v可通过兰德-皮尔森提出的速度历程曲线求解：

pagenumber_ebook=46,pagenumber_book=29

式中，T为爆轰波到达微元的时间，根据炸药爆速及起爆点与微元的距离计算；τ为时间常数，τ=A1mv0/pCJ+A2，A1、A2为常数，m为微元质量。

药型罩微元满足运动方程，有

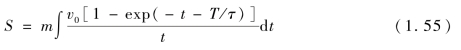
pagenumber_ebook=47,pagenumber_book=30

式中，S为微元面积。

由式（1.54）可以计算出不同区域药型罩微元极限压垮速度v0。偏转角δ也采用式（1.53）的形式，压垮角β、t时刻射流位置l、射流质量mj可分别表述为

pagenumber_ebook=47,pagenumber_book=30

式中，v′0和T′分别为v和T对药型罩微元x的导数；A=λ+δ；r1为药型罩微元的纵坐标；tc为药型罩微元碰撞时间；ρL为药型罩密度。

2.杆式射流成形条件

从本质上讲，杆式射流是具有一定速度梯度、无明显射流和杵体之分的射流。设计杆式射流聚能装药时，应对比其与常规聚能射流的差异，再分析杆式射流成形条件。总的来说，杆式射流成形应遵循以下3方面原则。

1）较小杵体质量

根据PER扩展理论，假设药型罩材料是非黏性不可压缩流体，罩壁很薄，微元与微元之间无相互作用，且药型罩微元速度在一定的时间内从零增加至压合速度v0。药型罩的压垮过程如图1.25所示。

根据经典聚能射流形成理论，射流和杵体质量表达式为

pagenumber_ebook=47,pagenumber_book=30

式中，dm、dmj和dms分别为药型罩、射流和杵体微元质量。其中，压合角β主要由药型罩锥角决定，其值越大，射流质量越大，相应的杵体质量则越小，因此形成杆式射流应采用大压合角药型罩。根据装药结构，相对于罩顶部微元，越接近底部的微元有效药量越小，得不到充分加速，大部分形成杵体。因此，为减小杵体质量和增大其速度，往往将药型罩设计成变壁厚结构，即从顶部到底部厚度逐渐减小，且装药直径大于药型罩直径。

pagenumber_ebook=48,pagenumber_book=31

图1.25　药型罩压垮过程

2）较小头、尾速度差

根据射流形成理论，射流和杵体速度vj、vs分别表述为

pagenumber_ebook=48,pagenumber_book=31

式中，α和δ分别为药型罩半锥角和偏转角。

设η为微元头、尾速度之比，可表述为

pagenumber_ebook=48,pagenumber_book=31

对于一定形状的药型罩，药型罩半锥角α在点P是一个定值，偏转角δ是与药型罩、炸药等参数相关的量，对于点P也是确定的，因此η只与β相关。随着β增大，η先减小后增大，即η存在一个最小值。为了降低射流头、尾速度差，需要将微元的压合角β控制在η取得最小值附近。

3）较大射流整体速度

在炸药类型及聚能装药结构确定的情况下，影响射流速度的主要因素包括起爆点位置、药型罩壁厚和药型罩半锥角等。减小药型罩厚度和半锥角能够有效提高射流速度，但同时会显著降低射流质量和直径。

根据式（1.61），在装药及药型罩结构确定的条件下，采用平面和环形起爆方式可有效提高射流速度。与中心点起爆相比，平面和环形起爆可有效降低爆轰波阵面与药型罩法线间的夹角，一方面可提高罩微元压合速度v0，另一方面可降低微元偏转角δ，从而降低微元压合角β，提高射流速度和射流质量。

因此，为了提高射流整体速度，应采用平面起爆或环形起爆。提高射流整体速度，降低射流头、尾速度差都与压合角β相关，但两者对β的取值要求是矛盾的。为保证杆式射流具有较高速度，以及较小的头尾速度差，设计药型罩和起爆点时需要将药型罩微元的β值控制在一个合适范围内。