爆炸成型弹丸是长径比为4~8、速度为1 500~3 000 m/s的恒速杆。爆炸成型弹丸在侵彻过程中会出现变形和侵蚀,且撞击速度较低,因此材料强度对侵彻过程影响较大。爆炸成型弹丸侵彻过程常以长杆侵蚀侵彻公式为基础,本节主要介绍长杆侵蚀侵彻理论模型和Allen-Rogers侵彻模型。第三阶段出现在长杆被完全侵蚀后,称为二次侵彻或残余塑性流动阶段。当ρj=ρt=ρ时,得到相对侵彻深度公式可表述为爆炸成型弹丸侵彻实验结果及模型预测曲线如图1.30所示。......
2023-06-18
大锥角、球缺形及回旋双曲线形药型罩,在聚能装药的作用下会被压垮,闭合形成具有较高质心速度(1 500~3 000 m/s)和一定结构形状的弹丸,即爆炸成型弹丸,以稳定飞行姿态与目标作用,对目标造成毁伤。
1.爆炸成型弹丸成形参数
炸药爆炸后,冲击波和爆轰产物作用于药型罩。药型罩上任一微元如图1.20所示,厚度为h,该微元表面积dA可表述为
![]()
式中,rθ、rφ为微元曲率半径;![]() 为微元单位法向矢量。
为微元单位法向矢量。

图1.20 典型球缺形药型罩微元
设气体产物压力为P=P(t),微元在药型罩与气体产物的相互作用下受到冲击压力P,并获得速度v,即
![]()
式中,dm为微元质量,可表述为
dm=ρhdAn
在轴对称条件下,基本矢量可表述为分量形式

式中,x和r分别表示轴向和径向分量;i和j分别为x和r方向上的单位矢量。
各方向微元速度分量为

由以上分析可知,爆炸成型弹丸的形状主要由沿药型罩速度分量的分布决定,且显著受药型罩外形、药型罩半锥角α和厚度h的影响。
2.爆炸成型弹丸成形条件
聚能装药被雷管引爆后,药型罩被压合,分别形成速度较高的射流和运行较慢的杵体,最后彼此分离。一般来说,射流质量约占药型罩总质量的15%,其余部分形成杵体。当药型罩锥角增大时,向内压合部分显著减少,相应地射流和杵体之间速度差也随之减小。研究表明,当半锥角接近75°时,射流和杵体速度几乎相同,如图1.21所示,将形成爆炸成型弹丸。
1)大锥角或回转曲线形药型罩
根据定常流体力学成形理论,射流和杵体的速度比为
![]()
药型罩形成爆炸成型弹丸时,可认为射流头部与尾部速度近似相等,此时
![]()
式中,α为药型罩半锥角;β为药型罩压垮角。β的经验公式表述为
![]()
其中
ω=0.1α(λ-0.228)2+0.029α+4.49(λ-0.16)2+2.83
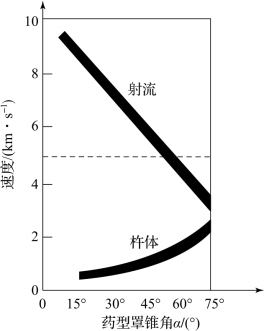
图1.21 锥角对射流和杵体速度的影响
式中,λ为药型罩微元的相对位置,大锥角药型罩大约仅有直径的73%有效,所以0~0.73为λ的有效区间。取中间值0.36,根据式(1.40)和式(1.41)计算出当药型罩锥角为137°时,射流和杵体合一,形成爆炸成型弹丸。
2)球缺形药型罩
球缺形药型罩的几何参数如图1.22所示,表面曲线方程表述为

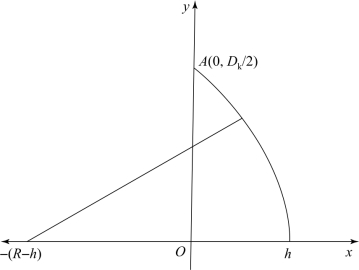
图1.22 球缺形药型罩几何参数
将A点坐标(0,Dk/2)代入式(1.42)得
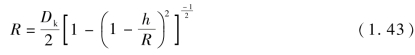
球缺形药型罩的斜率为

或者
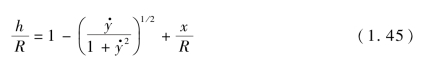
过球缺形药型罩口部作外切锥,参照锥形药型罩,若形成爆炸成型弹丸,其对应锥角应大于137°。考虑到大锥角药型罩只有(0~0.73)Dk部分形成爆炸成型弹丸,因此,球缺形药型罩口部锥角的下限应该使2y/Dk=0.73,该锥角为137°。
依据以上分析,球缺形药型罩口部锥角为120°。若口部锥角为120°~137°,根据式(1.43)和式(1.45)得到球缺形药型罩的曲率半径为
![]()
当球缺形药型罩曲率半径小于式(1.46)时,会降低药型罩形成爆炸成型弹丸的效率。当曲率半径偏离式(1.46)过多时,则会导致无法形成爆炸成型弹丸。
有关活性毁伤增强聚能战斗部技术的文章

爆炸成型弹丸是长径比为4~8、速度为1 500~3 000 m/s的恒速杆。爆炸成型弹丸在侵彻过程中会出现变形和侵蚀,且撞击速度较低,因此材料强度对侵彻过程影响较大。爆炸成型弹丸侵彻过程常以长杆侵蚀侵彻公式为基础,本节主要介绍长杆侵蚀侵彻理论模型和Allen-Rogers侵彻模型。第三阶段出现在长杆被完全侵蚀后,称为二次侵彻或残余塑性流动阶段。当ρj=ρt=ρ时,得到相对侵彻深度公式可表述为爆炸成型弹丸侵彻实验结果及模型预测曲线如图1.30所示。......
2023-06-18

图1.13射流成形定常流动模型建立射流成形的定常流体力学理论,所作假设如下:爆轰波到达药型罩表面,微元以大小和方向不变的压合速度运动;各微元速度v0及变形角δ相等;变形过程中罩长度不变,即AC=BC。......
2023-06-18

总的来说,杆式射流成形应遵循以下3方面原则。图1.25药型罩压垮过程2)较小头、尾速度差根据射流形成理论,射流和杵体速度vj、vs分别表述为式中,α和δ分别为药型罩半锥角和偏转角。......
2023-06-18

几种常用板(片)材的成型温度见表6-1。三辊压光机是板(片)材冷却、压光、定厚度的重要设备,其工艺性能直接决定产品平整度和光亮度。为了使板材缓慢冷却,防止因内应力造成板材翘曲变形,三辊压光机的三个辊筒加热是关键。模唇厚度并不等于板材厚度,这是由于熔料离模膨胀、牵引拉伸和冷却收缩,使厚度发生变化。一般模唇厚度要大于板材厚度的10%~20%。如果板材厚度达不到要求,可调节口模温度,也可调节阻力块和口模间隙。......
2023-06-15

多种成型加工缺陷,是受模具结构的影响而产生的。1)技术要求:内光栅底部厚度为1.5mm,内、外圆柱壁厚为0.9mm。脱模时带齿内圆柱壁的脱模力很大,脱模机构如设计不当,将会使内光栅产生严重变形,甚至脱模时会将注塑件撕破。图7-20 内光栅2.注塑件的脱模斜度对注塑件上缺陷痕迹的影响注塑件脱模斜度的选取,会直接影响到注塑件脱模力的大小,进而可能导致注塑件翘曲、裂纹和变形等缺陷的产生。......
2023-06-30

同时,对于我们理解、认知当下各种纷繁复杂的时尚及其他社会现象也有着很强的启发性和导向作用,但也应该看到他的理论中依然存在着片面性和局限性。笔者认为这不仅是一种选词的谨慎和坚持,更多的还是源于作者本人思想上的矛盾性,因为如果他承认了自己的后现代主义立场,就会消解自身理论建构的整体性和终极意义,这肯定不是他想要的结果。......
2023-06-18

所谓直接烧结自由成形是,用激光束烧结塑料粉,直接得到塑料成形件。显然,用激光烧结自由成形陶瓷器件时,只能采用第二种间接烧结自由成形工艺。采用有机粘结剂时,激光烧结成形件应进行两次加热后处理:第一次加热,烧除粘结剂;第二次加热,用高温烧结得到最终的“褐件”。......
2023-06-15

休闲活动是完全个性化的,其本质是自由。休闲活动对大学生的心理健康调节来说,具有以下功能:(一)消除紧张,缓解压力,提高效率适度的压力对人的发展有促进作用,但过度或长期的压力无疑会造成身心疲乏。体育、音乐、绘画等休闲活动,能使人产生愉悦的心情,增强生理的承受能力,从而巩固身体的健康。......
2023-11-01
相关推荐