第二次世界大战期间,坦克等装甲战车大量投入战场,推动了聚能效应及反坦克弹药技术发展,包括反坦克枪榴弹、反坦克炮射破甲弹、反坦克火箭破甲弹等。目前,国内外普遍采用大曲率铝合金药型罩,利用装药爆炸形成大尺寸聚能侵彻体,其侵彻混凝土过程中的高压、高温引发局部气化效应,实现大孔径侵彻。......
2025-09-29
1.定常流体力学成形理论
射流形成过程比较复杂,炸药爆轰波到达药型罩壁面的初始压力远大于药型罩金属材料强度。因此,在射流成形过程中可以忽略材料强度对药型罩运动的影响,而把药型罩看成“理想流体”,同时忽略射流成形过程中的材料体积压缩,将射流成形过程中药型罩金属材料当作“理想不可压缩流体”。
在以上假设的基础上,以锥形罩为例,研究射流成形过程。射流成形定常流动模型如图1.13所示,α为半锥角,OC为罩壁初始位置。假设微元G在E处碰撞时,爆轰波到达A点,当爆轰波到达C点时,微元A到达轴线B,即碰撞点从E点到了B点,碰撞点运动速度以v1表示。以爆轰波到达微元A点为例,认为A点开始运动速度为v0(称为压合速度),方向与罩表面法线成δ角(称为变形角),并将BC与轴线的夹角β称为压合角或压垮角。

图1.13 射流成形定常流动模型
建立射流成形的定常流体力学理论,所作假设如下:
(1)爆轰波到达药型罩表面,微元以大小和方向不变的压合速度运动;
(2)各微元速度v0及变形角δ相等;
(3)变形过程中罩长度不变,即AC=BC。
根据上述假定和三角形关系,AE平行于CB,∠AEB=∠CBH=β,即各微元的压合角相等。在静坐标下,杵以速度vs运动,射流以速度vj运动。如果把坐标系建立在碰撞点,并观察药型罩压垮过程,可看到药型罩材料以速度v2流向碰撞点,在碰撞点处分散为射流和杵体,并向相反方向运动。
依据伯努利方程,在动坐标下,罩壁以速度v2流向碰撞点,仍以相同速度向左和向右离去。与此同时,在碰撞点观察时,微元运动不随时间变化,这种运动状态不随时间而变的过程称为定常过程。
在静坐标系下

射流质量为mj,杵质量为ms,由质量守恒定律有
![]()
式中,m为微元质量。
依据轴线方向的动量守恒,有
![]()
将式(1.3)代入式(1.4),可得

对于碰撞点速度v1和罩壁相对速度v2,在三角形ABE中有

因此

代入式(1.1)和式(1.2),可得

式(1.5)、式(1.6)、式(1.9)和式(1.10)即定常理想不可压缩流体条件下的射流和杵体的质量和速度表达式。
2.准定常流体力学成形理论
一维准定常射流成形理论认为锥形罩闭合速度从罩顶到罩底逐渐减小。图1.14所示为闭合速度为变量时的药型罩闭合过程。当爆轰波沿罩表面APQ从P点传播到Q点时,P点的微元闭合到J点,而原来在P′点的微元以相较于P点慢的闭合速度开始闭合,仅达到M点。如果它们以相同的闭合速度闭合,那么当P点到达J点时,P′点将到达N点。假如所有微元的闭合速度都是常数,那么罩表面将持续保持锥形发生变形,![]() 即直线。然而,由于P′点的闭合速度相较于P点更慢,所以罩表面不再保持直线,而是以图1.14所示
即直线。然而,由于P′点的闭合速度相较于P点更慢,所以罩表面不再保持直线,而是以图1.14所示![]() 曲线进行闭合。压合角β大于稳态压合角β+。微元不是垂直于其表面运动,而是沿着与表面法线呈一定角度δ的方向运动,该角度为变形角,也称为泰勒(Taylor)抛射角。根据图1.14所示的几何关系,泰勒抛射角表述为
曲线进行闭合。压合角β大于稳态压合角β+。微元不是垂直于其表面运动,而是沿着与表面法线呈一定角度δ的方向运动,该角度为变形角,也称为泰勒(Taylor)抛射角。根据图1.14所示的几何关系,泰勒抛射角表述为

式中,ue为爆轰波经过罩表面的速度。

图1.14 闭合速度为变量时的药型罩闭合过程
在碰撞点J处建立坐标系,各参量的几何关系如图1.15所示。药型罩轴线沿JR方向,OJ为向轴线运动的微元矢量,该微元的速度为OR=v0,动坐标系的速度为JR=v1。在图1.15中,由正弦定理可以得到

式(1.12)表明,当v0为常数时,准定常理论与定常流体力学理论相同。

图1.15 碰撞点处的几何关系
在静坐标系中,射流和杵的速度分别为
vj=v1+v2
vs=v1-v2
将式(1.12)代入,通过三角函数计算可得

将式(1.11)代入式(1.13)和式(1.14),可得到

依据动量和质量守恒定理,可得到射流和杵的质量表达式。设药型罩微元质量为dm,dmj和dms分别为射流和杵的质量,则

式(1.15)~式(1.18)分别表示锥形罩各微元的速度和质量,且均与锥顶角2α、爆速D、压合角β和压合速度v0有关。为了获得β,设图1.14中M点的坐标为(r,z),P′点的坐标为(x,xtanα),如图1.16所示,其中

式中,t为起爆后任意时间;t0为爆轰波阵面到达药型罩P′点处的时间。

图1.16 微元坐标方向
在任意时刻t,可通过微分∂r/∂z求得被压垮的药型罩轮廓线斜率。当微元到达锥轴线处时,r=0,由式(1.20)可得

同时,r=0,∂r/∂z的值正是tanβ。微分式(1.19)和式(1.20)得

式中,v′0表示v0对x的偏导数。
3.射流速度分布
在药型罩压合过程中,罩体内、外层压合速度是不同的。在药型罩微元向轴线运动的过程中,微元运动方向与轴线夹角为θ,与轴线交点为O,如图1.17所示。图中λ3表示微元内表面到O点的距离,λ2表示微元外表面到O点的距离。微元的密度、质量和动能分别用ρ、M和T表示。作如下假设:
(1)微元为理想不可压缩流体;(https://www.chuimin.cn)
(2)爆轰波到达药型罩壁面后,该微元速度立即到达平均压合速度v0,大小和运动方向保持不变;
(3)罩微元运动时,宽度a保持不变,且令a=1。
在图1.17中,微元初始位置为l1,运动至l2时,厚度增大。l3为微元内表面到达轴线时的状态,厚度增加至最大值λ0。微元运动时,平均压合速度保持不变,即微元动能不变,但是其厚度方向、各层的速度在发生变化。

图1.17 微元压合过程示意
微元厚度为λ2-λ3,微元质量可表述为
![]()
当其运动至轴线时,M=πλ2
0ρsinθ,可得
![]()
在罩内、外层之间取某一层,距O点距离为λ,内、外层间微元质量为μ,且
![]()
以质量μ和时间t为坐标,该坐标称为物质坐标。某一层速度即μ不变的条件下,该层λ值随时间的变化率,通过偏导数可表述为
v=∂λ/∂t
微元外层和内层速度分别表述为

因各层速度不同,故各层的动能不同,设λ处的动能为dT,则
![]()
式(1.25)对t求偏导数,得
![]()
因此
λ2v2=λv
令y=λ/λ0,y2=λ2/λ0,得

将v2代入dT表达式,得
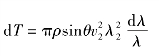
微元总动能T为各层动能之和,因此![]()

由式(1.24),可得又有![]() 代入得
代入得

由式(1.23)和式(1.25)有

将式(1.27)和式(1.28)中的![]() 代入式(1.26)得
代入式(1.26)得

而![]() 为平均压合速度,将T代入上式,得到
为平均压合速度,将T代入上式,得到
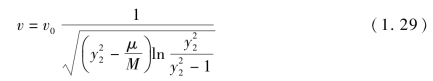
由于v与坐标λ方向相反,故v0和v均为负值。式(1.29)就是在给定时间t、某层μ处速度v的表达式。
以μ=0和μ=M代入,即得微元外层速度v2和内层速度v3:

根据轴对称理想不可压缩流体理论分析,药型罩的轴对称压合和平面对称压合不同,在微元向轴线运动的过程中,能量由外层向内层集中,且越靠近对称轴,能量集中越快。当微元运动到轴线附近时,由于微元内表面附近压力急剧升高,微元变宽,且其运动方向改变,最后内层金属变成沿轴向运动的射流。
轴对称压合时,罩壁内、外速度差仅在微元接近轴线时才较为明显,而在大部分运动时间内,与平面对称压合过程接近。因此,基于平面对称压合的准定常流体力学理论,通过实验修正,可对射流速度进行分析。
4.射流成形临界条件
药型罩壁相对压合速度v2与压合速度v0的几何关系如图1.18所示。当罩壁压合时,在动坐标系中,罩壁相对压合速度为v2,在碰撞点E附近拐弯,分成方向相反的射流和杵体。需要注意的是,流动必须为亚音速,若v2大于材料音速,则在碰撞点处产生冲击波,材料仅发生折射而不翻转,则无法形成射流。因此药型罩压合形成射流的临界条件为
![]()
式中,a为药型罩材料音速。

图1.18 v2与v0的几何关系
为了便于分析,假设压合速度v0垂直于变形后的罩壁,则
![]()
由此可知,当v0增大或β减小时,可能使v2增大,以致v2大于a,而不能形成射流。但是v0也不能太小,否则同样不能形成射流,因为此时材料的强度不能忽略。v0垂直于轴线的分速度以v4表示,则
![]()
碰撞速度应为v4的2倍,碰撞时所产生的动压力应超过材料的动态屈服强度σy,由此可得另一个极限条件
![]()
当外加压力稍大于动态屈服强度时,材料尚不能当作流体。当冲击压力达到10倍动态屈服强度时,材料可按流体处理,则可得
![]()
根据式(1.31)、式(1.33)和式(1.34),可得铜罩形成射流的极限条件,如图1.19所示,可划分为4个区域。

图1.19 铜罩形成射流的极限条件
Ⅰ—v4太小,无射流;Ⅱ—非流体力学区;Ⅲ—流体力学区,有射流;Ⅳ—v2超音速,无射流
相关文章

第二次世界大战期间,坦克等装甲战车大量投入战场,推动了聚能效应及反坦克弹药技术发展,包括反坦克枪榴弹、反坦克炮射破甲弹、反坦克火箭破甲弹等。目前,国内外普遍采用大曲率铝合金药型罩,利用装药爆炸形成大尺寸聚能侵彻体,其侵彻混凝土过程中的高压、高温引发局部气化效应,实现大孔径侵彻。......
2025-09-29

同时,对于我们理解、认知当下各种纷繁复杂的时尚及其他社会现象也有着很强的启发性和导向作用,但也应该看到他的理论中依然存在着片面性和局限性。笔者认为这不仅是一种选词的谨慎和坚持,更多的还是源于作者本人思想上的矛盾性,因为如果他承认了自己的后现代主义立场,就会消解自身理论建构的整体性和终极意义,这肯定不是他想要的结果。......
2025-09-29

药型罩底部到靶板表面的距离称为炸高,选择合理的炸高对聚能效应,尤其是射流毁伤威力的发挥至关重要。图1.7典型聚能装药结构从毁伤机理上看,射流头部速度很高,远超靶板材料的声速,碰撞靶板时在接触面上产生冲击波,分别传入射流和靶板中,碰撞点处产生极高的压力和温度,致使靶板材料发生熔化和破坏,在碰撞点附近产生高压、高温、高应变率区域,称为三高区。图1.8开坑阶段准定常阶段。图1.9准定常阶段......
2025-09-29

所谓直接烧结自由成形是,用激光束烧结塑料粉,直接得到塑料成形件。显然,用激光烧结自由成形陶瓷器件时,只能采用第二种间接烧结自由成形工艺。采用有机粘结剂时,激光烧结成形件应进行两次加热后处理:第一次加热,烧除粘结剂;第二次加热,用高温烧结得到最终的“褐件”。......
2025-09-29

氯霉素是广谱抗生素,主要用于伤寒杆菌、痢疾杆菌、脑膜炎球菌、肺炎球菌感染的治疗,亦可用于立克次体感染的治疗。氯霉素分子中有2个手性碳原子,所以存在4个旋光异构体,化学结构式为:上面4个异构体中仅1R, 2R-(-)有抗菌活性,为临床使用的氯霉素。氯霉素为白色或微黄色的针状、长片状结晶或结晶性粉末,味苦。立即加入乙醇38 mL,于35℃搅拌反应5 h。若反应未达终点,可补加适量的乙酸酐和醋酸钠继续酰化。......
2025-09-29

图3-50 喷印的银触点图3-51 喷印的银迹线图3-52 喷印的太阳能电图3-53 有机太阳能电池的典型结构池的汇流条和集流体有机薄膜太阳能电池中的主要结构件的喷印成形工艺过程如下:基板处理在超声波浴池中用清洁剂清洗基板30min,再用去离子水漂净,然后,用已过滤的异丙醇进行超声波处理15min,并用氧等离子体进行处理。图3-54是喷印成形的太阳能电池。......
2025-09-29

单键中普通平键和半圆键应用最广,故本节仅介绍平键和半圆键的公差与配合。平键连接采用基轴制,国标GB/T1095—2003《平键键槽的剖面尺寸》对键宽只规定了一种公差带h9,通过改变轴槽和轮毂槽宽度构成了三种不同性质的配合。......
2025-09-29

巴比妥为长时间作用的催眠药,是第一个巴比妥类药物,主要用于神经过度兴奋、狂躁或忧虑引起的失眠。巴比妥化学名为5, 5-二乙基巴比妥酸,结构式为:巴比妥为白色结晶或结晶性粉末,无臭,味微苦。在装有搅拌器、滴液漏斗及球形冷凝管的250 mL三颈瓶中,加入无水乙醇75 mL,分次加入金属钠6 g。第二步:巴比妥的制备仪器:三颈瓶、球形冷凝管、蒸馏装置1套、量筒。反应完毕,将回流装置改为蒸馏装置。......
2025-09-29
相关推荐