力矩分配法适用于计算无节点线位移的刚架和连续梁。这样的状态称为一个力矩分配单元。 用力矩分配法计算图1.8-6所示结构。图1.8-7 图1.假定当L1=6m,L2=8m,L3=5m,该梁弯矩分配系数μBA及B支座的不平衡弯矩ΔM应与下列( )组数据相近。C支座左右两端分配系数为0.4,0.6;固端弯矩为150kN·m、-120kN·m,试问该梁进行二次弯矩重分配,B、C支座的弯矩接近( )组数据。......
2023-08-28
现以图16-5(a)所示只有一个刚结点的两跨连续梁为例,来说明力矩分配法的基本原理。
为了计算该结构,在结构没有承受荷载前,先在刚结点B处加上控制转动的附加刚臂(抗转支座)将刚结点B锁住,此时刚结点B处无任何位移,相当于固定端约束。原结构被附加刚臂分隔为两个单跨超静定梁AB和BC。此时,在荷载作用下其变形曲线如图16-5(b)所示。各单跨超静定梁在荷载作用下的两端弯矩![]()
![]() 称为固端弯矩,固端弯矩可由表查得。同时在附加刚臂上产生了约束力矩
称为固端弯矩,固端弯矩可由表查得。同时在附加刚臂上产生了约束力矩![]() ,此约束力矩
,此约束力矩![]() 可以用刚结点B的力矩平衡条件
可以用刚结点B的力矩平衡条件![]() 求得
求得
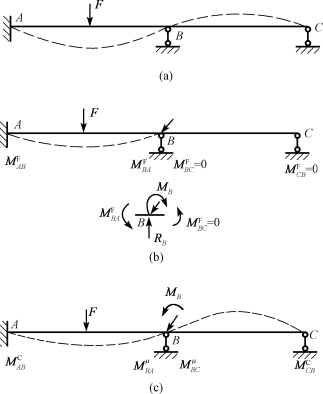
图16-5 力矩分配法基本原理
![]()
即附加刚臂上的约束力矩![]() 等于刚结点B处各杆近端固端弯矩之和。以顺时针转向为正,反之为负。
等于刚结点B处各杆近端固端弯矩之和。以顺时针转向为正,反之为负。
为了使图16-5(b)所示附加刚臂的结构能和原结构的变形和受力等同,必须放松附加刚臂,使刚结点B产生转角φB,或抵消附加刚臂上的约束力矩![]() 。为此,在刚结点B处加上一个与约束力矩
。为此,在刚结点B处加上一个与约束力矩![]() 大小相等,转向相反的力矩
大小相等,转向相反的力矩![]() ,即约束力矩的负值,如图16-5(c)所示。
,即约束力矩的负值,如图16-5(c)所示。![]() 将使刚结点B产生原结构的转角φB。
将使刚结点B产生原结构的转角φB。
由以上分析可见,图16-5(a)所示连续梁受力和变形情况,应等于图16-5(b)和图16-5(c)所示两种情况的叠加。也就是说,要计算原结构各杆件的杆端弯矩,应分别计算图16-5(b)所示情况的杆端弯矩即固端弯矩MF和图16-5(c)所示情况的杆端弯矩(即分配弯矩Mμ、传递弯矩MC),然后将它们叠加起来就是最终弯矩。对于图16-5(c)所示情况的杆端弯矩计算,由以上分析可知,只要把作用在刚结点B的力偶矩![]() 按各杆的分配系数分配于各杆的B端(近端)得到分配弯矩,再由各杆B端的分配弯矩分别乘以传递系数传向远端得到传递弯矩即可。最终杆端弯矩
按各杆的分配系数分配于各杆的B端(近端)得到分配弯矩,再由各杆B端的分配弯矩分别乘以传递系数传向远端得到传递弯矩即可。最终杆端弯矩![]() 。
。
以上就是力矩分配法的基本思路,概括来说:先在B结点加上附加刚臂阻止B结点转动,把连续梁看成两个单跨粱,求出各杆的固端弯矩MF,此时刚臂承受不平衡力矩![]() (各杆固端弯矩的代数和),然后去掉附加刚臂,即相当于在B结点作用一个反向的不平衡力矩
(各杆固端弯矩的代数和),然后去掉附加刚臂,即相当于在B结点作用一个反向的不平衡力矩![]() ,求出各杆端的分配弯矩Mμ及传递弯矩MC,叠加各杆端弯矩即得原连续梁各杆端的最后弯矩。用力矩分配法做题时,不必绘制图16-5(b)、(c),而是按一定的格式进行计算,即可十分清晰地说明整个计算过程。
,求出各杆端的分配弯矩Mμ及传递弯矩MC,叠加各杆端弯矩即得原连续梁各杆端的最后弯矩。用力矩分配法做题时,不必绘制图16-5(b)、(c),而是按一定的格式进行计算,即可十分清晰地说明整个计算过程。
【例16-1】用力矩分配法计算图16-6(a)所示连续梁的弯矩。EI为常数。
解:(1)计算分配系数。两杆在B结点刚性连接,A端为链杆支座,C端为固定,两杆转动刚度分别为
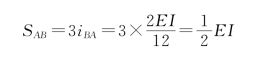

图16-6 例16-1图
![]()
因此

∑μ=1,说明计算无误。
(2)计算固端弯矩和约束力矩。先在结点B加一附加刚臂[图16-6(b)]使结点B不能转动,此步骤常称为“固定结点”。此时各杆端产生的固端弯矩,由表查得各固端弯矩为
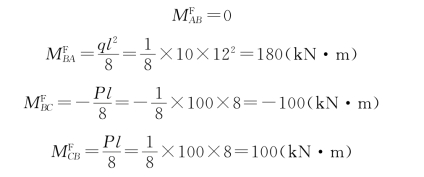
连接于结点B的各固端弯矩之和等于约束力矩![]() :
:
![]()
(3)计算分配弯矩、传递弯矩。为了消除约束力矩![]() ,应在结点B处加入一个与它大小相等方向相反的力矩
,应在结点B处加入一个与它大小相等方向相反的力矩![]() [图16-6(c)],在约束力矩被消除的过程中,结点B即逐渐转动到无附加约束时的自然位置,故此步骤常简称为“放松结点”。
[图16-6(c)],在约束力矩被消除的过程中,结点B即逐渐转动到无附加约束时的自然位置,故此步骤常简称为“放松结点”。
将分配系数乘以约束力矩的负值即得分配弯矩:
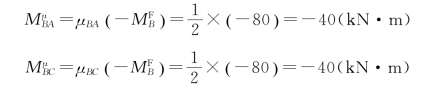
将传递系数乘以分配弯矩即得传递弯矩:

(4)计算各杆端的最终弯矩:
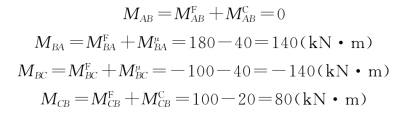
(5)画弯矩图:根据各杆端的最终弯矩和已知荷载,用叠加法画弯矩图如图16-6(d)所示。
实际计算时,可以直接在结构上进行(也可以列表计算),如图16-6(e)所示。分配弯矩下面画一横线,表示该结点已经平衡(即附加刚臂上的约束力矩已被抵消),用箭头表示分配弯矩的传递方向。杆端弯矩的最终结果下面画双横线。
有关建筑力学(第2版)的文章

力矩分配法适用于计算无节点线位移的刚架和连续梁。这样的状态称为一个力矩分配单元。 用力矩分配法计算图1.8-6所示结构。图1.8-7 图1.假定当L1=6m,L2=8m,L3=5m,该梁弯矩分配系数μBA及B支座的不平衡弯矩ΔM应与下列( )组数据相近。C支座左右两端分配系数为0.4,0.6;固端弯矩为150kN·m、-120kN·m,试问该梁进行二次弯矩重分配,B、C支座的弯矩接近( )组数据。......
2023-08-28

图15-352.分配系数、分配弯矩图15-36所示的刚架,由于刚结点上力偶矩mA的作用而发生变形,刚结点A发生转角θA而达到平衡。杆件AB在刚结点A的分配系数μAB等于杆体AB的转动刚度与交于A点的各杆转动刚度之和的比值。同一刚结点各杆分配系数之间存在下列关系:以上的计算可简单表述为:将作用在刚结点A上的力偶矩按各杆的分配系数直接分配于各杆的A端。远端为自由端时,近端力矩、远端力矩均等于零。故将远端弯矩称为传递弯矩。......
2023-08-26

对于近端,用固端弯矩叠加分配弯矩;对于远端,用固端弯矩叠加传递弯矩。用力矩分配法计算图15-40所示的连续梁,并作出M图。悬臂杆DF去掉后,节点D成为铰节点,不需进行力矩分配,简化了计算。......
2023-08-26

局部反馈校正也称反馈校正,是将校正装置接于系统局部闭环的反馈通道之中,用以改善系统的控制性能。因此,通常采用工程近似计算的方法,即在具有局部反馈校正的情况下采用近似的闭环传递函数,以便于校正计算。如图6-16所示为具有局部反馈校正的反馈控制系统。图6-16具有局部反馈校正的反馈控制系统一般将满足式的频率范围称为被校正频段,满足式的频率范围称为不被校正频段。......
2023-06-28

由于CNN模型的网络深度并不能无限增加,当网络深度增加到一定的层数之后,继续增加反而会导致模型出现退化,即引起模型的识别性能降低,因此VGG模型的网络深度被确定为16层和19层,对应的VGG-16模型和VGG-19模型成为VGG模型的常用代表。VGG-16模型包含13个卷积层和3个FC层,即一共有16个卷积/FC层。VGG-16模型全部使用3×3卷积核,步长均为1。VGG-16模型最后的输出层是Softmax层,输出当前样本对所有类别的归属概率值。图6-9不同深度的VGG模型结构......
2023-06-29

上节用只有一个刚结点的结构介绍了力矩分配法的基本概念。对于具有两个以上刚结点的结构也可用力矩分配法进行计算。多结点力矩分配法的计算步骤如下:求出汇交于各结点每一杆端的力矩分配系数μij,并确定其传递系数Cij。固定刚结点B和C,各杆的固端弯矩为其余各固端弯矩均为零。刚结点B的约束力矩除固端弯矩外,还包括传递过来的传递弯矩,即所以传递弯矩为进行第二轮计算。用力矩分配法作图16-8所示刚架的弯矩图。......
2023-06-16

它是一种能够自动连续、快速、准确地完成信息存储、数值计算、数据处理和过程控制等多种功能的电子机器。所谓硬件子系统系指构成计算机系统的物理元件或物理装置,它包括组成计算机的各部件和外部设备。微机与传统的计算机并无本质区别。它也是由运算器、控制器、存储器和输入/输出接口等部件组成。图1-39列出了计算机硬件系统和软件系统的组成。反之,没有软件或没有完善良好的软件,计算机就无法工作或不能高效率地工作。......
2023-08-26

(一)基因工程介绍和基本原理基因工程是现代生物学研究的重要手段,它是综合运用多项现代生物技术,实现DNA分子人工定向改造的一种技术方法。基因工程除了可以构建各种重组质粒外,还可以对基因组DNA进行改造,在基因组的特定位置点删除、替换、插入外源基因序列,构建各种基因工程菌。基因工程技术涉及以下步骤:从生物体的基因组中分离目的DNA序列(基因)。这通常包括DNA的纯化技术、酶促消化或机械切割等。......
2023-11-06
相关推荐