其中 θA、θB分别表示 A 端和 B 端的转角，其转向以顺时针为正；ΔA、ΔB分别表示 A、B 两端沿杆轴垂直方向的线位移，其方向以绕另一端顺时针方向转动为正；ΔAB表示 A、B 两端的相对线位移，β＝ΔAB/l 表示直线 A′B′ 与 AB 的平行线的交角，称为弦转角，并规定以顺时针方向转动为正。......
2023-08-30
杆端位移对杆端力的影响
【摘要】：已知A端的转角位移为φA，B端的转角位移为φB，A、B两端在垂直于杆轴方向上的相对线位移为ΔAB。现求由其引起的杆端内力。关于它们的正负号规定如下：杆端转角φA、φB均以顺时针方向为正；杆件两端的相对线位移ΔAB则以使整个杆件顺时针方向转动为正。再以弯矩符号MAB代替X1，用MBA代替X2，上式便可写成这就是由杆端位移φA、φB和ΔAB所引起的杆端弯矩的计算公式。此外，由静力平衡条件还可求出杆端剪力。
如图15-6（a）所示两端固定的单跨超静定梁，两端的支座发生了位移。已知A端的转角位移为φA，B端的转角位移为φB，A、B两端在垂直于杆轴方向上的相对线位移（亦简称侧移）为ΔAB（AB杆沿水平方向和竖直方向的平行移动，均不引起杆端内力，故只需考虑A、B两点间的相对线位移的影响）。现求由其引起的杆端内力。关于它们的正负号规定如下：
（1）杆端转角φA、φB均以顺时针方向为正；杆件两端的相对线位移ΔAB则以使整个杆件顺时针方向转动为正。
（2）杆端弯矩规定以对杆端以顺时针方向旋转为正（对结点或支座则以反时针方向旋转为正）。
（3）杆端剪力的正负号规定同前。
图15-6所示的杆端弯矩及位移均以正值标出。
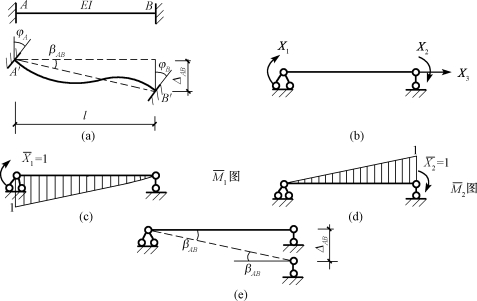
图15-6 两端固定的单跨超静定受力分析
用力法求解这一问题时，可取如图15-6（b）所示的简支梁为基本结构，其多余约束反力为杆端弯矩X1、X2和轴力X3。目前，可以认为轴向约束反力X3对梁的弯矩并没有影响，可不予考虑，只需求解X1和X2。
根据沿X1和X2方向的位移条件，可建立力法方程如下：_
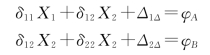
式中的系数和自由项均可按前面的方法求得。作出
图[图15-6（c）]、
图[图15-6（d）]后，由图乘法可得系数
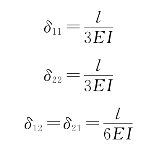
自由项Δ1Δ和Δ2Δ是由于支座移动所引起的简支梁两端的转角位移，由图15-6（e）可见，支座转动并不使基本结构产生任何转角位移；而支座两端相对线位移所引起的两端转角为
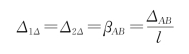
式中，βAB称为弦转角，亦以顺时针方向为正。
将以上所求得的系数和自由项代入力法方程解得
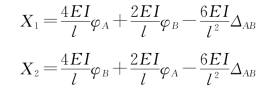
为了方便，令
称为杆件的线刚度。再以弯矩符号MAB代替X1，用MBA代替X2，上式便可写成
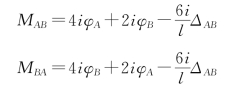
这就是由杆端位移φA、φB和ΔAB所引起的杆端弯矩的计算公式。此外，由静力平衡条件还可求出杆端剪力。即
将MAB、MBA代入上式即得
有关建筑力学（第2版）的文章
- 详细阅读
-
掌握杆杠原理：力与位移计算公式及杠杆类型详解详细阅读
杠杆就是一个简单的梁，能够铰接在旋转关节或者杠杆支点上。力与位移的计算公式如下：力（L÷X）×FA=FG位移（X÷L）×MA=MG图1-3二级杠杆图1-4三级杠杆图1-4所示为一个三级杠杆。三级杠杆与二级杠杆的不同之处在于施力点的位置以及作用力的方向。在这类杠杆中，施力点位于杠杆支点和力产生点之间。图1-5杠杆与边杆直角杠杆的角度是90°，属于一级杠杆，其最典型的应用是在连杆系统中改变施力的方向。......
2023-06-25
-
压杆稳定：什么是压杆稳定？详细阅读
对于细长的压杆却表现出性质完全不同的破坏现象。1925 年苏联的莫兹尔桥及1940 年美国的塔科马桥的破坏都是因压杆失稳而造成的重大工程事故。下面讨论细长压杆的稳定性问题。使中心受压直杆的直线平衡形式，由稳定平衡转变为不稳定平衡时所受的轴向压力，称为临界载荷，或简称为临界力，用Pcr表示。本章主要讨论中心受压直杆的稳定问题，研究确定压杆临界力的方法、压杆的稳定计算和提高压杆承载能力的措施。......
2023-06-19
-
如何计算钢结构中的压杆力？详细阅读
9-1 如图9-11 所示正方形桁架，各杆各截面的弯曲刚度均为EI，且均为细长杆。9-2 如图9-12 所示两端球形铰支细长压杆，弹性模量E=200 GPa。图9-13题9-39-4 如图9-14 所示矩形截面压杆，有三种支持方式。其他各项条件相同，只须计算各压杆的相当长度。图9-14题9-4图图9-15题9-5图9-6 如图9-16 所示托架，实心圆截面杆BD 的直径为d=32 mm，长度l=1 m，两端可视为球铰，材料为Q235，E=200 GPa，σS=240 MPa，λP=100，λS=60，临界应力经验公式为σcr=a-bλ，其中a=310 MPa，b=1.14 MPa。......
2023-06-19
-
平面杆系结构位移计算的一般公式详细阅读
式即为平面杆系结构位移计算的一般公式。分别写出虚设力状态上的外力和内力在实际变形状态相应的位移和变形上所做的虚功，并由虚功原理得到结构位移计算的一般公式。将式代入式得__式为静定结构在荷载作用下位移计算的一般公式。......
2023-06-16
-
轴向拉压对杆的变形：胡克定律简析详细阅读
反之，在轴向压力作用下，将引起轴向的缩短和横向的增大。因此，必须研究杆件的变形。与上述两种绝对变形相对应的纵向线应变为横向线应变线应变表示的是杆件的相对变形。即式（4-5）称为虎克定律。常数E 称为材料的弹性模量，其值随材料而异，可由试验测定。试求整个杆的变形量。......
2023-06-19
-
欧拉公式：细长压杆临界力计算方法详细阅读
下面介绍不同约束条件下压杆的临界力计算公式。两端铰支细长杆的临界力计算公式——欧拉公式。从欧拉公式可以看出，细长压杆的临界力Fcr与压杆的弯曲刚度成正比，而与杆长l的平方成反比。杆端为其他约束的细长压杆，其临界力计算公式可参考前面的方法导出，也可以采用类比的方法得到。经验表明，具有相同挠曲线形状的压杆，其临界力计算公式也相同。......
2023-06-16
-
现场总线与工业以太网应用技术-端到端通信详细阅读
在互联网中，任何两台通信的主机之间，从源端到目的端的信道都是由一段一段的点到点通信线路组成的。图8-15 传输层端到端通信点到点通信是由网络互联层来实现的，网络互联层只屏蔽了不同网络之间的差异，构建了一个逻辑上的通信网络，因此它只解决了数据通信问题。端到端通信是建立在点到点通信基础之上的，它是比网络互联层通信更高一级的通信方式，用于完成应用程序（进程）之间的通信。端到端的通信是由传输层来实现的。......
2023-11-20
相关推荐