变形体的虚功原理及其相应的单位力法并不仅限于求解静定结构的位移，同样也适用于求解超静定结构的位移，问题是如何使计算得到简化。这两个弯矩图都是经超静定结构的力法计算所得。若按图 6-39和图 6-39进行图乘计算，得结果与前相同，说明方法正确，即计算超静定结构的位移可采用去除多余约束后的静定结构建立虚拟力状态，把问题转化为静定结构的位移计算，这将使计算工作大为简化。......
2023-08-30
基本概念与思路：位移法解决超静定结构的方法
【摘要】：力法是以多余未知力为基本未知量，位移法则是以某些结点的位移作为基本未知量，这是力法和位移法的基本区别之一。为了说明位移法的基本概念，现以图15-1所示超静定刚架为例来分析其位移。综上所述，位移法的基本思路是：分析结构的结点位移情况，确定基本未知量。利用平衡条件建立位移法基本方程，求解基本未知量。
应用力法求解超静定结构，是以多余约束力为基本未知量，取与原结构受力等效，位移协调的静定结构为基本结构，由位移协调条件建立基本方程求解基本未知力，再利用静力平衡条件进一步求出结构中的其他内力、支座反力和位移。然而，在一定的外因作用下，结构的内力与位移之间具有恒定的关系，即：确定的内力只与确定的位移相对应。因此，在分析超静定结构时，也可以把结构中的某些位移作为基本未知量，首先将这些位移求解出来，然后，再据此计算结构的内力，这便是位移法。力法是以多余未知力为基本未知量，位移法则是以某些结点的位移（包括结点的角位移和结点的线位移）作为基本未知量，这是力法和位移法的基本区别之一。
利用位移法计算超静定结构的方法有两种：一是直接利用平衡条件建立位移法方程；二是和力法类似，建立位移法的典型方程。其实这两种方法本质上是一样的，而前一种方法思路清晰、过程简单、更容易理解，所以本章主要介绍前一种方法。
为了说明位移法的基本概念，现以图15-1（a）所示超静定刚架（各杆EI为常数）为例来分析其位移。在荷载F作用下，刚架将发生图中虚线所示的变形，刚结点B处的两端均发生相同的转角位移φB。在结构分析中，对于受弯杆件来说，通常都略去杆件轴向变形和剪切变形的影响，且认为弯曲变形是微小的，因而可假定结构中各杆两端之间的距离在变形前后仍保持不变，因而结点B处没有线位移。在图15-1所示刚架中，由于固定支座A和固定铰支座C处都不能产生移动，而B结点与A、C两结点之间的距离又保持不变，因此，B结点处没有线位移而只有角位移φB。
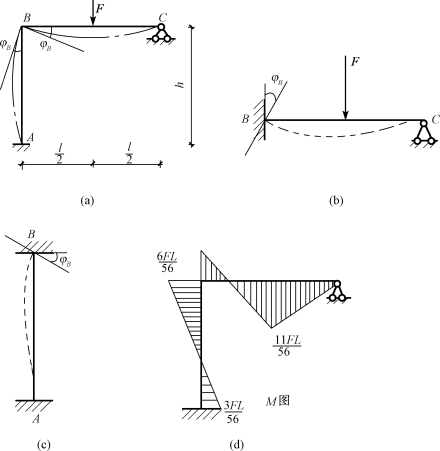
图15-1 超静定刚架受力分析
如何根据B点的角位移来确定各杆的内力呢？图15-1所示刚架，是由两根杆件组成的，现在我们先对每根杆件进行研究。如果将刚结点B看成固定支座，则BC杆可视为一根一端固定一端铰支的单跨超静定梁，其上除了受到荷载F的作用外，在固定支座B处还发生了转角位移φB，如图15-1（b）所示；同理，BA杆则可视为两端固定的单跨超静定梁，而在固定端B处发生了转角φB，如图15-1（c）所示。根据表14-1可写出各杆的杆端弯矩如下（注意到BC杆既有荷载，又有结点角位移，故应叠加）：
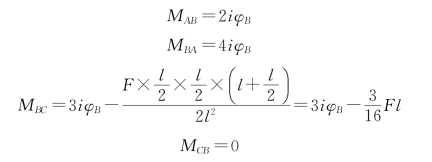
以上各式表示等截面直杆杆端力与杆端位移之间的关系，即用结点B处的角位移φB表示的杆端弯矩方程，所以又称为转角位移方程。由于φB是未知量，因而各杆端的杆端弯矩尚不能确定。为了确定φB，可以利用刚性结点B处力矩的代数和等于零的平衡条件，即由∑MB＝0可得
MBC＋MBA＝0
将MBC、MBA表达式代入上式，求得
再将iφB代回各杆端弯矩式得到
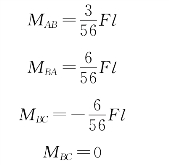
据此便可以作出该刚架的弯矩图，如图15-1（d）所示。
综上所述，位移法的基本思路是：
（1）分析结构的结点位移情况，确定基本未知量。
（2）将结构的各杆拆分为单跨超静定梁，查表14-1列出各杆杆端弯矩的表达式。
（3）利用平衡条件建立位移法基本方程，求解基本未知量。
（4）将求出的基本未知量代回杆端弯矩的表达式计算各杆的杆端弯矩。
（5）作内力图。
有关建筑力学（第2版）的文章
- 详细阅读
-
用位移法计算连续梁与超静定刚架详细阅读
位移法计算连续梁及超静定刚架一般步骤如下：确定基本未知量和基本结构。用位移法计算时，只有节点转角基本未知量，故仅需建立刚节点处的力矩平衡方程，即可求解出全部未知量，进而计算杆端弯矩，绘制出内力图。此连续梁只有一个刚节点B的转角位移θB，如图15-32所示。列各杆杆端弯矩计算式。用位移法计算图15-34所示的超静定刚架，并作出弯矩图。......
2023-08-26
-
结构力学：静定和超静定平面刚架的计算方法详细阅读
杆件轴线及荷载作用线均处在同一平面内的刚架，称为平面刚架。在工程中实际应用的刚架，多数是超静定的，静定刚架较少采用。图3-112.静定平面刚架计算静定刚架的内力通常有弯矩、剪力和轴力，其计算方法原则上与静定梁的计算相同。......
2023-08-30
-
用力法求解超静定梁的方法和步骤详细阅读
计算超静定梁的位移时，通常忽略轴力和剪力的影响，只考虑弯矩的影响。因而系数及自由项按照下列公式计算：试用力法作图14-13所示单跨超静定梁的弯矩图。此梁具有三个多余约束，为三次超静定。将以上各值代入力法方程，而在前两式中消去后，得解以上方程组求得由力法方程的第三式求解X3时，可以看出，按不同的假设有不同的结果。......
2023-06-16
-
超静定结构的特性及优化方法详细阅读
超静定结构与静定结构相比，具有以下一些重要特性。了解这些特性，有助于加深对超静定结构的认识，并更好地应用它们。超静定结构的内力单由静力平衡条件不能全部确定，还需要同时考虑位移条件。所以，超静定结构的内力与结构的材料性质以及杆件截面尺寸有关。在超静定结构中，任何上述因素作用，通常都会引起内力。因此超静定结构比静定结构具有较强的防护突然破坏能力。在设计防护结构时，应该选择超静定结构。......
2023-06-16
-
特性,超静定结构-结构力学详细阅读
超静定结构与静定结构对比，具有以下一些重要特性。了解这些特性，有助于加深对超静定结构的认识，并更好地应用。超静定结构的这一特性，在一定条件下会带来不利影响，例如连续梁可能由于地基不均匀沉陷而产生过大的附加内力。但超静定结构的内力单由平衡条件则无法全部确定，还必须考虑变形条件才能确定其解答，因此其内力数值与材料性质和截面尺寸有关。因此，从军事及抗震方面来看，超静定结构具有较强的防御能力。......
2023-08-30
-
结构力学中6.5.2支座位移对超静定结构的影详细阅读
由图 6-37容易看出，因基本结构是静定的，在支座移动因素作用下并不引起内力，故超静定结构的最终内力只与多余未知力有关。最终弯矩为：对于 n 次超静定结构，可表示为： 试绘制图 6-38所示梁在已知支座位移作用下的弯矩图。由上例可以看出，超静定结构在支座位移作用下的内力和反力项中包含了截面的刚度，说明它们与杆件刚度的绝对值成正比。......
2023-08-30
-
超静定结构的概念-结构力学书详细阅读
在前面各章中，已经详细地讨论了静定结构的计算问题，静定结构的全部反力和内力可由静力平衡条件确定。超静定结构的应用范围很广，图6-1 所示为一些工程中常见的超静定结构类型。图6-1常见的超静定结构从本章开始，我们将讨论超静定结构的计算问题。按照线弹性的计算理论，超静定结构的计算方法主要有以下两种：力法。力法和位移法是超静定结构计算的基本方法。......
2023-08-30
相关推荐