下面结合三次超静定的刚架来进一步说明用力法解多次超静定结构的一般原理和力法典型方程的建立。上述方程组在组成上具有一定的规律性，不论超静定结构的类型、超静定次数以及所选的基本结构如何，所得的方程都具有式（6-2）的形式，故称之为力法的典型方程。力法方程最后一项位移 ΔiF称为自由项。......
2023-08-30
力法典型方程与柔度系数计算方法
【摘要】：根据叠加原理，式可写成以下形式：图14-12位移条件式就是为求解多余未知力X1和X2所需要建立的力法方程。对于高次超静定问题，其力法方程也可类似推出。当原结构在去掉多余约束处的已知位移为零时，其力法方程为方程中的系数称为柔度系数，位于主对角线上的系数δii称为主系数，在主对角线两侧的系数δij称为副系数，Δ1P称为自由项。由于基本体系是静定的，所以力法方程中各系数和自由项都可以按照上一单元位移计算的方法求出。
以上我们以一次超静定梁为例，说明了力法原理。下面我们讨论多次超静定的情况。如图14-11（a）所示的刚架为二次超静定结构。下面以B点支座的水平和竖直方向反力X1、X2为多余未知力，确定基本结构，如图14-11（b）所示。按上述力法原理，基本结构在给定荷载和多余未知力X1、X2共同作用下，其内力和变形应等同于原结构的内力和变形。原结构在铰支座B点处沿多余力X1和X2方向的位移（或称为基本结构上与X1和X2相应的位移）都应为零，即
上式就是求解多余未知力X1和X2的位移条件。
图14-11 基本结构的确定
以Δ1P表示基本结构上多余未知力X1的作用点沿其作用方向，由于荷载单独作用时所产生的位移；Δ2P表示基本结构上多余未知力X2的作用点沿其作用方向，由于荷载单独作用时所产生的位移；δij表示基本结构上Xi的作用点沿其作用方向，由于
单独作用时所产生的位移，如图14-12所示。根据叠加原理，式（14-2）可写成以下形式：
图14-12 位移条件
式（14-3）就是为求解多余未知力X1和X2所需要建立的力法方程。其物理意义是：在基本结构上，由于全部的多余未知力和已知荷载的共同作用，在去掉多余约束处的位移应与原结构中相应的位移相等。在本例中等于零。
在计算时，我们首先要求得式（14-3）中的系数和自由项，然后代入式（14-3），即可求出X1和X2，剩下的问题就是静定结构的计算问题了。
对于高次超静定问题，其力法方程也可类似推出。若为n次超静定结构，用力法方程计算时，可去掉n个多余约束，得到静定的基本结构，在去掉的多余约束处代以n个多余未知力，可根据n个已知的位移条件建立n个关于多余未知力的方程。当原结构在去掉多余约束处的已知位移为零时，其力法方程为
方程中的系数称为柔度系数，位于主对角线上的系数δii称为主系数，在主对角线两侧的系数δij称为副系数，Δ1P称为自由项。可以证明δij＝δji。
由于基本体系是静定的，所以力法方程中各系数和自由项都可以按照上一单元位移计算的方法求出。
在基本未知量X1，X2，X3，…，Xn求得后，可以由叠加原理求得超静定结构任一截面的内力
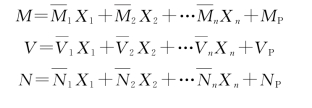
有关建筑力学（第2版）的文章
- 详细阅读
-
压杆柔度与临界应力的欧拉公式计算方法详细阅读
于是临界应力可写为令则上式为计算压杆临界应力的欧拉公式，式中λ称为压杆的柔度。从式（9-3）还可以看出，压杆的柔度值越大，则其临界应力越小，压杆就越容易失稳。因此，欧拉公式的适用范围应当是压杆的临界应力σcr不超过材料的比例极限σP，即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则故欧拉公式的适用范围为上式表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。......
2023-06-16
-
工程地下水（第2版）中用灵敏度分析法计算导水详细阅读
图2-43灵敏度分析方法计算含水层水文地质参数程序框图如果T和μ＊的初始值特别差，程序可能不会收敛。由上述可知，应用灵敏度分析、从最小二乘法判断中求得最佳的导水系数和贮水系数，从而使实际的抽水试验资料自动拟合泰斯公式，该法也可在更复杂的水文地质条件下应用。......
2023-09-23
-
测量平差程序设计：误差方程与法方程系数对应关详细阅读
所以为了节省内存，平差示例程序中采用一维数组保存法方程系数，并且只保存主对角线以上的数值，因而法方程系数阵称为上三角阵。例如pibidi中bi、di在误差方程系数数组中的下标分别是2、4，填充到法方程系数阵二维数组变量中的下标就是（2，4）。......
2023-10-22
-
水文地质勘察渗透系数计算方法详细阅读
渗入深度z可通过试验前在试坑外3～4m处以及实验后在内环中心处,各钻1孔取土样,对比不同的岩(土)湿度的变化来确定。SL 345—2007《水利水电工程注水试验规程》在试坑双环注水试验中规定,土的渗透系数按式进行。坑内水头一般采用10cm;Hα为试验土层的毛细上升高度,cm,查表5-7得Hk后令Hα=2Hk,同样的,当0.5Hα值超过了试坑的开挖深度,应取试坑的深度值;z为从坑底算起的渗入深度,cm;16.67为单位换算系数。......
2023-09-18
-
丢番图方程解析：破解整系数代数方程，取得惊人详细阅读
丢番图致力于研究简单代数方程的求解问题，并且取得很了不起的成果。在现代数学里，丢番图方程所指的是考虑整数解时的整系数代数方程。上一章我们提到一个丢番图方程：x2-3y2=1。我们看到，有些丢番图方程没有（整数）解，而有的则有无穷多组解。也就是说，我们已经找出了这个丢番图方程的所有解。......
2023-10-30
-
电阻损耗及系数计算方法介绍详细阅读
Kf是考虑交变电流趋肤效应和邻近效应对电阻的影响而引入的系数，即当导体中通过交变电流时，因趋肤效应和邻近效应而产生的附加损耗。则电阻损耗为式中：γ——材料的密度； m——材料的质量。电阻率ρ是温度θ的函数，其表达式为式中：ρ0、ρ20——0℃、200℃时的电阻率（Ω·m）； α、β——电阻温度系数。......
2023-06-30
-
压边力和拉深力的计算方法详细阅读
压边力的大小应允许在一定范围内调节。一般来说，随着拉深系数的减小，压边力许可调节范围减小，这对拉深工作是不利的，因为当压边力过大时，就会产生破裂，压边力过小时，会产生起皱，即拉深的工艺稳定性不好。相反，拉深系数较大时，压边力可调节范围增大，拉深工艺稳定性较好。表4-48 采用或不采用压边装置的条件为了更准确地估算是否需要压边装置，还应考虑拉深系数的大小。......
2023-06-26
相关推荐