静定结构和超静定结构的概念已在第十一章中作过介绍。相反，一个结构，如果其所有的未知力不能仅用平衡方程确定，则这种结构称为超静定结构。此连续梁有四个支座反力，而平衡方程却只有三个，仅用平衡方程不能求解，因此截面内力也就无法确定，所以它是一个超静定结构。图14-2超静定结构的类型......
2023-06-16
力法原理：去除多余约束求解未知力
【摘要】：基本结构在原有荷载和多余未知力共同作用下的体系称为力法的基本体系。如果能设法求出符合实际受力情况的X1，也就是支座B处的真实反力，那么，基本体系的内力和变形就与原结构在荷载作用下的情况完全一样，从而将超静定结构问题转化为静定结构问题。用公式可表示为通过这个例子，可以看出力法的基本思路是：去掉多余约束，以多余未知力代替，再根据原结构的位移条件建立力法方程，并解出多余未知力。图14-10力法的基本原理
图14-10（a）所示为单跨超静定梁，它是具有一个多余约束的超静定结构。如果把支座B去掉，在去掉多余约束B支座处以未知力X1代替，原结构就变成静定结构，说明它是一次超静定结构。此时梁上作用有均布荷载q和集中力X1，如图14-10（b）所示。这种在去掉多余约束后所得到的静定结构，称为原结构的基本结构，代替多余约束的未知力X1称为多余未知力。基本结构在原有荷载和多余未知力共同作用下的体系称为力法的基本体系。如果能设法求出符合实际受力情况的X1，也就是支座B处的真实反力，那么，基本体系的内力和变形就与原结构在荷载作用下的情况完全一样，从而将超静定结构问题转化为静定结构问题。
如何求出X1？仅靠平衡条件是无法求出的。因为在基本体系中截取的任何隔离体上除了X1之外还有三个未知内力或者反力，故平衡方程的总数少于未知力的总数，其解答是不定的。确定多余未知力X1，必须考虑变形条件以建立补充方程。为此对比原结构与基本体系的变形情况。原结构在支座B处由于多余约束的作用而不可能有竖向位移；虽然基本体系上多余的约束已经被去掉，但是如果其受力和变形情况与原结构完全一致，则在荷载q和多余未知力X1共同作用下，其B点的竖向位移（即沿着力X1方向上的位移）ΔB也应该等于零，即ΔB＝0。
这就是用以确定X1的变形条件或者位移条件。
我们可以把基本体系分解成分别由荷载和多余未知力单独作用在基本结构上的这两种情况的叠加，即图14-10（c）和（e）的叠加。
用Δ11和Δ1P表示基本结构在未知力X1和荷载q单独作用时B点沿X1方向的位移，其符号都以沿着假定的X1方向为正，如图14-10（c）、（e）所示，两个下标的含义依次为第一个表示位移的地点和方向，第二个表示产生位移的原因。根据叠加原理，可得
ΔB＝Δ11＋Δ1P＝0
若用δ11表示当X1＝1时B点沿X1方向的位移，则有Δ11＝δ11X1。这里δ11的物理意义为：基本结构上，由于
的作用，在X1的作用点，沿X1方向产生的位移。于是上述位移条件可写成
上式是含有多余未知力X1的位移方程，称为力法方程。式中δ11称作系数；Δ1P称为自由项，它们都表示静定结构在已知荷载作用下的位移，完全可用前面知识求得，因而多余未知力X1即可由此方程解出。利用力法方程求出X1后就完成了把超静定结构转换成静定结构来计算的过程。
上述计算超静定结构的方法称为力法。它的基本特点就是以多余未知力作为基本未知量，根据所去掉的多余约束处相应的位移条件，建立关于多余未知力的方程或方程组，我们称这样的方程（或方程组）为力法典型方程，简称力法方程。解此方程或方程组即可求出多余未知力。
下面计算系数δ11和自由项Δ1P，为了计算δ11和Δ1P，可分别绘出基本结构在
和q作用下的弯矩图
图和MP图，如图14-10（d）、（f）所示，然后利用图乘法计算这些位移。
求δ11时应为
图和
图相乘，即
图自乘：
求Δ1P时应为
图和MP图相乘：
把δ11和Δ1P代入式（14-1）得
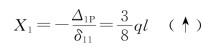
计算结果X1为正值，表示开始时假设的X1方向是正确的（向上）。
多余未知力X1求出后，其内力可按静定结构的方法进行分析，也可利用叠加法计算。即将X1＝1单独作用下的弯矩图M1乘以X1后与荷载单独作用下的弯矩图MP叠加。用公式可表示为
通过这个例子，可以看出力法的基本思路是：去掉多余约束，以多余未知力代替，再根据原结构的位移条件建立力法方程，并解出多余未知力。这样就把超静定问题转化为静定问题了。
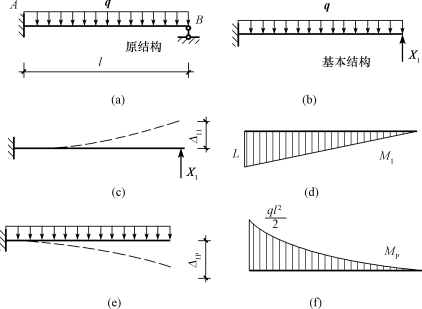
图14-10 力法的基本原理
有关建筑力学（第2版）的文章
- 详细阅读
-
位移法基本未知量求解方法详细阅读
如前所述，位移法是以结点位移作为基本未知量。结点位移有两种，即结点角位移（转角）和结点线位移，因此，必须先确定位移法的基本未知量的数目。如图15-2所示的刚架，其结构内部只有B、C两个刚性结点，因此也就只有两个角位移未知量。图15-4铰化结点判定法（一）图15-5铰化结点判定法（二）综上所述，位移法基本未知量的数目，等于结构中结点角位移的数目和独立结点线位移的数目之和。......
2023-06-16
-
虚功原理和单位力法解析-结构力学详细阅读
变形体系的虚功原理可表述为：变形体系处于平衡的必要和充分条件是，对于符合变形体系约束条件的任意微小的连续虚位移，变形体系上所有外力所做的虚功总和外W ，等于变形体系各微段截面上的内力在其虚变形上所做的虚功总和U变。虚功原理更一般地表示为：由以上可见，虚功原理需要涉及两个状态，取一个状态的外力和内力，取另一个状态的位移和变形。如果位移是虚设的，则称为虚位移原理；如果外力是虚设的，则称为虚力原理。......
2023-08-30
-
保险合同法：保证平等权益及法律约束力详细阅读
投保人和保险人作为依照保险合同建立的保险法律关系的双方当事人，其法律地位是平等的，任何一方不得把自己的意志强加给对方。双方达成的保险合同具有法律约束力，任何单位和个人不得干预。按照保险合同，投保人应向保险人交付约定的保险费，保险人则应在约定的保险事故发生时，履行赔偿或给付保险金的义务。保险合同之所以能够发生法律效力，受到国家法律的保护，是因为所签订的保险合同是合法的。......
2023-08-10
-
强化监督管理的约束力详细阅读
加强党员干警的教育管理是增强党的凝聚力、战斗力的重要保证。通过三大系列制度的修改、完善，堵塞管理漏洞，形成用制度管人管事的运行机制，规范、约束党员干警的行为。层层签订“创先争优目标考核责任书、党风廉政建设责任书、车辆安全管理责任书、网络安全运行责任书”，建立奖惩处理机制，严格执行“一岗双责”和“治庸问责”规定，实行责任过错追究制。......
2023-07-27
-
结构力学,力法基本原理解析详细阅读
如图 6-8所示，X1表示被去掉的多余约束的反力，暂时是未知的，故称为多余约束未知力或力法的基本未知量。由于 δ11和 Δ1F是静定结构在已知力作用下的位移，均可按前章所述计算位移的方法求得，因此，解上述方程，可求得多余未知力X1。......
2023-08-30
-
力法基本原理-建筑力学（第3版）详细阅读
力法是计算超静定结构最基本的方法，下面先用一个例子说明力法的基本原理。这个静定梁称为原超静定梁的基本结构。若用Δ1q和Δ11分别表示荷载q和多余未知力X1单独作用下基本结构在X1作用处沿X1方向产生的位移，则由叠加原理根据位移条件可得下列方程：若X1＝1，在X1方向产生的位移为δ11，则有Δ11＝δ11X1，于是式可以写成这就是求解多余未知力的补充方程，称为力法方程。......
2023-08-26
-
弯曲力、顶件力与压料力分析详细阅读
弯曲力也是设计多工位级进模和选择压力机吨位的重要依据。弯曲力的大小不仅与毛坯尺寸、材料力学性能、凹模支点间的距离、弯曲半径、模具间隙等有关，而且与弯曲方式也有很大关系。图4-27 校正弯曲a）V形弯曲件 b）U形弯曲件表4-28 单位面积上的校正力 3.顶件力和压料力设有顶件装置或压料装置的弯曲件，其顶件力或压料力可近似取自由弯曲力的30%～80%，即式中 FQ———顶件力或压料力；F自———自由弯曲力。......
2023-06-26
相关推荐