首页理论教育图乘法的使用条件和公式详解

图乘法的使用条件和公式详解

2025-09-29 理论教育版权反馈

【摘要】：对于由多个弯曲刚度EI为常数的杆段组成的结构，用图乘法计算位移的公式为显然，图乘法是将积分运算问题简化为求图形的面积、形心和竖标的问题。需要说明的是，用图乘法计算位移时，梁和刚架的杆件必须满足以下条件：杆段的弯曲刚度EI为常数。下面给出了图乘运算中几种常见图形的面积及其形心位置，如图13-14所示。

在计算由荷载作用引起的梁和刚架的位移时，需要计算积分

式中，是两个弯矩方程的乘积。若在满足一定条件的情况下，能画出两种状态下的弯矩图，则上式可以转换为用弯矩图互乘的方法，即用图乘法代替积分运算，这样可使计算得到简化。现在对上面的积分式进行分析。

图13-13所示为直杆段AB的两个弯矩图，假设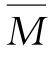 pagenumber_ebook=177,pagenumber_book=168 图为直线图形，M图为任意图形。

pagenumber_ebook=177,pagenumber_book=168

图13-13　直杆段AB的两个弯矩图

如果该杆截面的弯曲刚度EI为常数，则

由于 pagenumber_ebook=177,pagenumber_book=168 图为直线图形，所以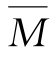图中某一点的纵坐标为这里tanα为常数，则有

pagenumber_ebook=177,pagenumber_book=168

式中，dA表示M图的微面积（图中阴影线部分的面积）；积分表示M图的面积对于y轴的静矩，它等于M图的面积A乘以其形心C到y轴的距离xC，即 pagenumber_ebook=177,pagenumber_book=168 。

所以

pagenumber_ebook=177,pagenumber_book=168

设M图的形心C所对应的 pagenumber_ebook=178,pagenumber_book=169 图中的竖标为yC，由图13-13可知xCtanα＝yC。

所以

pagenumber_ebook=178,pagenumber_book=169 (https://www.chuimin.cn)

式中，A为M图的面积；yC为M图的形心C所对应的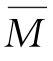 pagenumber_ebook=178,pagenumber_book=169 图中的竖标。

对于由多个弯曲刚度EI为常数的杆段组成的结构，用图乘法计算位移的公式为

pagenumber_ebook=178,pagenumber_book=169

显然，图乘法是将积分运算问题简化为求图形的面积、形心和竖标的问题。

需要说明的是，用图乘法计算位移时，梁和刚架的杆件必须满足以下条件：

（1）杆段的弯曲刚度EI为常数。

（2）杆段的轴线为直线。

（3）各杆段的M图和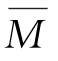 pagenumber_ebook=178,pagenumber_book=169 图中至少有一个为直线图形。

对于等截面直杆，前两个条件自然满足。至于第三个条件，虽然在均布荷载的作用下M图的形状是曲线形状，但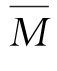 pagenumber_ebook=178,pagenumber_book=169 图却总是由直线段组成，只要分段考虑也可满足。于是，对于由等截面直杆段所构成的梁和刚架，在计算位移时均可应用图乘法。

应用图乘法时应注意：

（1）在图乘前要先对图形进行分段处理，保证两个图形中至少有一个是直线图形。

（2）A与yC是分别取自两个弯矩图，竖标yC必须取自直线图形。

（3）当A与yC在杆的同侧时，乘积AyC取正号；A与yC在杆的异侧时，乘积AyC取负号。

下面给出了图乘运算中几种常见图形的面积及其形心位置，如图13-14所示。在应用图示抛物线图形的公式时，必须注意曲线在顶点处的切线应与基线平行，即在顶点处剪力为零。

pagenumber_ebook=178,pagenumber_book=169

图13-14　各种图形的形心位置