杠杆就是一个简单的梁,能够铰接在旋转关节或者杠杆支点上。力与位移的计算公式如下:力(L÷X)×FA=FG位移(X÷L)×MA=MG图1-3二级杠杆图1-4三级杠杆图1-4所示为一个三级杠杆。三级杠杆与二级杠杆的不同之处在于施力点的位置以及作用力的方向。在这类杠杆中,施力点位于杠杆支点和力产生点之间。图1-5杠杆与边杆直角杠杆的角度是90°,属于一级杠杆,其最典型的应用是在连杆系统中改变施力的方向。......
2023-06-25
1.单位荷载法
现在,我们结合图13-7(a)所示刚架,讨论如何利用变形体虚功原理来建立计算平面杆件结构位移的一般公式。

图13-7 某刚架位移计算示意
图13-7(a)中虚线表示刚架在荷载、温度变化及支座移动等因素的作用下所发生的变形(C1、C2、C3表示支座的位移),这是结构的实际位移状态,简称实际状态。现在要求任一指定点K点沿任一指定方向k—k上的位移ΔK。
利用虚功原理求解这个问题,首先要确定两个彼此独立的状态,即力状态和位移状态。由于是求实际状态下结构的位移,所以应把结构的实际状态图[图13-7(a)]作为结构的位移状态。而力状态则可以根据所求位移来虚设。为了便于求出位移和简化计算,我们选取一个与所求位移相对应的虚单位荷载,即在K点沿k—k方向施加一个单位力![]() ,其箭头指向可以沿k—k任意假设,如图13-7(b)所示。这个力状态并不是实际原有的,而是一个虚设的状态,简称虚拟状态。
,其箭头指向可以沿k—k任意假设,如图13-7(b)所示。这个力状态并不是实际原有的,而是一个虚设的状态,简称虚拟状态。
在虚单位荷载![]() 作用下,结构将产生虚反力
作用下,结构将产生虚反力![]() 和虚内力
和虚内力![]() (弯矩)、
(弯矩)、![]() (剪力)、
(剪力)、![]() (轴力),它们构成了一个虚设力系。
(轴力),它们构成了一个虚设力系。
根据变形体系的虚功原理,计算以上两种状态中虚拟状态的外力和内力在相应的实际状态上所做的虚功。则有
![]()
因![]() ,故上式简化为
,故上式简化为
![]()
式中,ε、γ、k分别为实际状态中的轴向应变、剪切应变和弯曲应变。
式(13-1)即为平面杆系结构位移计算的一般公式。
由以上位移计算公式的建立过程,可归纳出用虚功原理求结构位移的基本方法:
(1)把结构在实际各种外因作用下的平衡状态作为位移状态,即实际变形状态。
(2)在拟求位移的某点处沿所求位移的方向上,施加与所求位移相应的单位荷载,以此作为结构的力状态,即虚设力状态。
(3)分别写出虚设力状态上的外力和内力在实际变形状态相应的位移和变形上所做的虚功,并由虚功原理得到结构位移计算的一般公式。_
我们把这种在沿所求位移方向施加一个单位力![]() 的位移计算方法称为单位荷载法。
的位移计算方法称为单位荷载法。
需要说明的是,上述平面杆系结构位移计算的一般公式,不仅适用于静定结构,也适用于超静定结构;不仅适用于弹性材料,也适用于非弹性材料;不仅适用于荷载作用下的位移计算,也适用于由温度变化、制造误差以及支座移动等因素影响下的位移计算。
2.虚单位荷载的设置
单位荷载法是计算结构位移的一般方法,其不仅可用于计算结构的线位移,也可以用来计算结构任何性质的位移,只要虚拟状态中所设虚单位荷载与所求的位移相对应,即保证广义力与广义位移的对应关系即可。现举出几种典型的虚拟状态如下:
(1)若计算的位移是结构上某一点沿某一方向的线位移,则应在该点沿该方向施加一个单位集中力,如图13-8(a)所示。
(2)若计算的位移是杆件某一截面的角位移,则应在该截面上施加一个单位集中力偶,如图13-8(b)所示。
(3)若计算的是桁架中某一杆件的角位移,则应在该杆件的两端施加一对与杆轴垂直的反向平行集中力,使其构成一个单位力偶,每个集中力的大小等于杆长的倒数,如图13-8(c)所示。
(4)若计算的位移是结构上某两点沿指定方向的相对线位移,则应在该两点沿指定方向施加一对反向共线的单位集中力,如图13-8(d)所示。
(5)若计算的位移是结构上某两个截面的相对角位移,则应在这两个截面上施加一对反向单位集中力偶,如图13-8(e)所示。
(6)若计算的是桁架中某两杆的相对角位移,则应在该两杆上施加两个方向相反的单位力偶,如图13-8(f)所示。
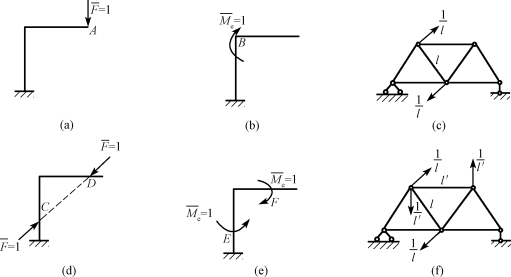
图13-8 虚单位荷载的设置
需要明确的是,虚拟状态中单位荷载的指向是可以任意假设的,若按式(13-1)计算出来的结果是正值,则表示实际位移的方向与虚拟荷载的方向相同,否则相反。
3.荷载作用下的位移计算公式
若静定结构的位移仅仅是由荷载作用引起的,没有支座位移的影响(即c=0),则式(13-1)可简化为
![]()
式中,微段的变形εds、γds、kds是由荷载引起的。
若用N、V、M表示实际位移状态中微段上由实际荷载产生的轴力、剪力和弯矩,在线弹性范围内,变形与内力有如下关系:
![]()
式中,EA、GA、EI分别为杆件的拉压刚度、剪切刚度、弯曲刚度;
K为剪力分布不均匀系数,其与截面形状有关。
将式(13-3)代入式(13-2)得__
![]()
式(13-4)为静定结构在荷载作用下位移计算的一般公式。式中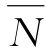 (轴力)、
(轴力)、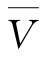 (剪力)、
(剪力)、 (弯矩)表示在虚拟状态中由广义单位荷载引起的虚内力,这些虚内力和原结构由实际荷载引起的内力,都可以通过静力平衡条件求得。
(弯矩)表示在虚拟状态中由广义单位荷载引起的虚内力,这些虚内力和原结构由实际荷载引起的内力,都可以通过静力平衡条件求得。
式(13-4)综合考虑了轴向变形、剪切变形和弯曲变形对结构位移的影响。在实际应用中,则根据不同形式的结构特性,对不同形式的结构分别采用不同的简化计算公式。
(1)对梁和刚架而言,弯曲变形是主要变形,而轴向变形和剪切变形对结构位移的影响很小,可以忽略不计。所以式(13-4)简化为

(2)对于桁架,由于各杆件均只有轴向变形,且每一杆件的轴力和截面面积沿杆长不变,所以式(13-4)简化为
![]()
(3)对于组合结构,梁式杆件主要承受弯矩,其变形主要是弯曲变形,可只考虑弯曲变形对位移的影响。而链杆只承受轴力,只有轴向变形,所以其位移计算公式简化为
![]()
(4)对于拱,当不考虑曲率的影响时,拱结构的位移可以近似地按式(13-5)来计算。通常情况下,只需考虑弯曲变形的影响,按式(13-5)计算,其结果已足够精确。仅在计算扁平拱的水平位移或者拱轴线与合理轴线接近时,才考虑轴向变形的影响,即
![]()
需要说明的是,在上述位移计算公式中,都没有考虑杆件的曲率对变形的影响,这对直杆是正确的,而对曲杆则是近似的。但是,在常用的结构中,如拱结构、曲梁和有曲杆的刚架等,这些结构中构件的曲率对变形的影响都很小,可以略去不计。
【例13-1】求图13-9(a)所示简支梁的中点C的竖向位移和截面B的转角。已知梁的弯曲刚度EI为常量。
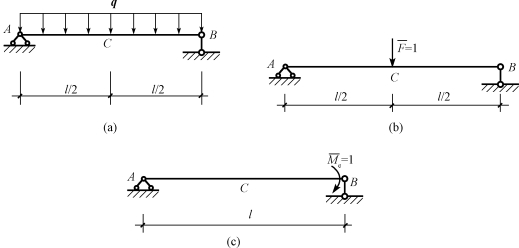
图13-9 例13-1图
解:(1)求点C的竖向位移_ΔCV。
在点C沿竖向施加单位力![]() ,作为虚拟力状态,如图13-9(b)所示。
,作为虚拟力状态,如图13-9(b)所示。
分别建立虚设荷载和实际荷载作用下梁的弯矩方程。取点A为坐标原点,当0≤x≤l/2时,有
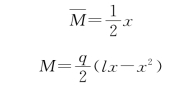
由于该梁C点左右对称,所以ΔCV只需计算一半,把结果乘2,即得

(2)求截面B的转角φB。
在B端施加一单位力偶![]() ,作为虚拟力状态,如图13-9(c)所示。
,作为虚拟力状态,如图13-9(c)所示。
分别建立虚设荷载和实际荷载作用下梁的弯矩方程。取A点为坐标原点,当0≤x≤l时,则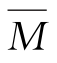 和M的方程是
和M的方程是
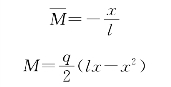
则根据公式可得
![]()
计算结果为负值,说明实际的转角φB与所设单位力偶的方向相反,即是逆时针方向。
【例13-2】求图13-10(a)所示刚架上点C的水平位移ΔCH,已知各杆的EI为常数。
解:在C点沿水平方向施加单位力![]() ,作为虚拟力状态,如图13-10(b)所示。分别建立虚设荷载和实际荷载作用下刚架各杆的弯矩方程。
,作为虚拟力状态,如图13-10(b)所示。分别建立虚设荷载和实际荷载作用下刚架各杆的弯矩方程。
AB杆
![]()
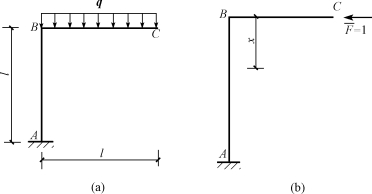
图13-10 例13-2图
BC杆
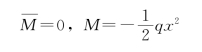
则点C的水平位移为
![]()
计算结果为负值,表明实际位移方向与所设单位荷载的方向相反。
【例13-3】求图13-11(a)所示桁架结点C的竖向位移。已知各杆的弹性模量均为E=2.1×105 MPa,截面面积A=12cm2。
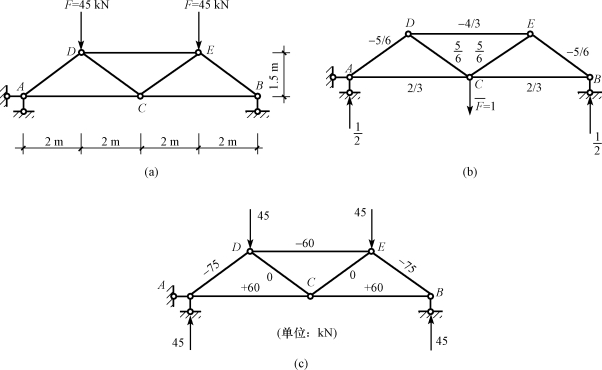
图13-11 例13-3图
解:在点C沿竖向施加单位力![]() 作为虚拟力状态,如图13-11(b)所示。
作为虚拟力状态,如图13-11(b)所示。
计算虚拟力状态的杆件内力如图13-11(b)所示。
计算实际状态的杆件内力如图13-11(c)所示。
具体计算过程列表进行,见表13-1。由于桁架及荷载的对称性,计算总和时,在表中只计算了半个桁架。杆DE的长度只取一半。最后求位移时乘以2。
表13-1 桁架结点竖向位移计算
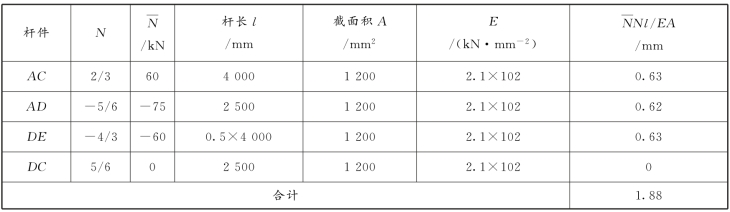
ΔCV=2×1.88=3.76(mm)(↓)
【例13-4】组合结构如图13-12(a)所示。其中CD、BD为二力杆,其拉压刚度为EA;AC为受弯杆件,其弯曲刚度为EI。在D点有集中荷载F作用。求D点的竖向位移ΔDV。

图13-12 例13-4图
解:在D点沿竖向施加单位力![]() 作为虚拟力状态如图13-12(b)所示。
作为虚拟力状态如图13-12(b)所示。
分别计算虚设荷载和实际荷载作用下链杆的轴力,如图13-12(c)、(d)所示,并建立受弯杆的弯矩方程。
BC杆
![]()
AB杆
![]()
求得D点的竖向位移为
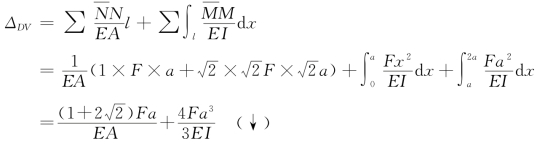
有关建筑力学(第2版)的文章

杠杆就是一个简单的梁,能够铰接在旋转关节或者杠杆支点上。力与位移的计算公式如下:力(L÷X)×FA=FG位移(X÷L)×MA=MG图1-3二级杠杆图1-4三级杠杆图1-4所示为一个三级杠杆。三级杠杆与二级杠杆的不同之处在于施力点的位置以及作用力的方向。在这类杠杆中,施力点位于杠杆支点和力产生点之间。图1-5杠杆与边杆直角杠杆的角度是90°,属于一级杠杆,其最典型的应用是在连杆系统中改变施力的方向。......
2023-06-25

已知A端的转角位移为φA,B端的转角位移为φB,A、B两端在垂直于杆轴方向上的相对线位移为ΔAB。现求由其引起的杆端内力。关于它们的正负号规定如下:杆端转角φA、φB均以顺时针方向为正;杆件两端的相对线位移ΔAB则以使整个杆件顺时针方向转动为正。再以弯矩符号MAB代替X1,用MBA代替X2,上式便可写成这就是由杆端位移φA、φB和ΔAB所引起的杆端弯矩的计算公式。此外,由静力平衡条件还可求出杆端剪力。......
2023-06-16

如果结构的结点有线位移,则称为有结点线位移结构。用位移法计算有结点线位移结构时,基本步骤与计算无结点线位移结构相同,其区别在于:在基本未知量中,含有结点线位移,故在写转角位移方程时要考虑线位移的影响。此刚架有一个刚结点B,其转角位移记作φB;有一个线位移,记作Δ,如图15-9所示。利用刚性结点的力矩平衡条件和产生线位移层的截面力平衡条件,建立位移法方程。......
2023-06-16

计算结果为正,表示ΔCx的方向与所设单位力的方向相同,即 ΔCx方向向右。 求图 5-17所示半圆弧三铰拱顶铰 C 两旁截面的相对转角。图5-17解:计算拱的位移,仅考虑弯矩对弯曲变形的影响,按公式计算。计算三铰拱受荷载及单位力偶作用时[见图 5-17、]的弯矩方程,应先求出支座反力,然后列出弯矩方程。此题由于三铰拱为对称结构,可只对拱的一半列出方程。......
2023-08-30

静定结构在支座移动时,只发生刚体位移,不产生内力和变形。这种位移可通过几何关系求得,也可应用单位力法进行计算。在式中,乘积的正负号规定为:当虚拟状态的支座反力与实际支座位移的方向一致时取正号,相反时取负号。 刚架的支座位移如图 5-19所示,试求 A 点的水平位移 ΔAx和 C 点左右截面的相对转角位移 θCC。......
2023-08-30

下面介绍不同约束条件下压杆的临界力计算公式。两端铰支细长杆的临界力计算公式——欧拉公式。从欧拉公式可以看出,细长压杆的临界力Fcr与压杆的弯曲刚度成正比,而与杆长l的平方成反比。杆端为其他约束的细长压杆,其临界力计算公式可参考前面的方法导出,也可以采用类比的方法得到。经验表明,具有相同挠曲线形状的压杆,其临界力计算公式也相同。......
2023-06-16

力矩分配法适用于计算无节点线位移的刚架和连续梁。这样的状态称为一个力矩分配单元。 用力矩分配法计算图1.8-6所示结构。图1.8-7 图1.假定当L1=6m,L2=8m,L3=5m,该梁弯矩分配系数μBA及B支座的不平衡弯矩ΔM应与下列( )组数据相近。C支座左右两端分配系数为0.4,0.6;固端弯矩为150kN·m、-120kN·m,试问该梁进行二次弯矩重分配,B、C支座的弯矩接近( )组数据。......
2023-08-28

利用虚功原理推导结构在荷载作用下位移计算的一般公式,首先要确定力状态和位移状态。利用式计算结构位移时,应根据结构的具体情况,只考虑其中一项或两项。这种用虚设单位荷载产生的内力,在实际状态荷载所引起的位移上做虚功,而利用虚功原理计算结构位移的方法,称为单位荷载法。单位荷载法计算位移公式适用于弹性材料和非弹性材料,可以用于计算静定结构的位移,也可以用于计算超静定结构的位移。......
2023-08-26
相关推荐