尤其是要学成一个高明的中医师，更非扎实地掌握好基本功不可。有人说理法方药是中医的基本功，又有人分成理论与临床功。能明确了这几方面，中医的基本功就可以确定了。在中医学术的理论体系中，最足以称基本的，莫过于藏象、病机、诊法、治则四端。藏象学说是研究人体脏腑生理功能、病理变化及其相互关系的学说。例如从藏象理论言，它是由脏腑、经络、精、气、神等主要知识构成的，因此，这些知识便是言藏象最基本的。......
2023-12-03
功的实现与虚象——功、实功、虚功详解
【摘要】：由上述可知，功包含了两个因素，即力和位移。图13-6广义力的虚功力状态；位移状态当力与位移的方向一致时，虚功为正值，当力与位移的方向相反时，虚功为负值。使力做虚功的位移，可以是荷载引起的位移、温度变化或支座移动等其他因素引起的位移，也可以是虚设的位移。
1.功
在力学中功的定义是：一个不变的集中力所做的功，等于该力的大小与其作用点沿力的作用线方向所发生的相应位移的乘积。当物体沿直线有位移Δ时[如图13-4（a）]，作用于物体的常力F在位移Δ上所做的功为W＝FΔCOSα。
图13-4 做功示意图
如果一对大小相等方向相反的力F作用在圆盘的A、B两点上，如图13-4（b）所示。设圆盘转动时，力F的大小不变而方向始终垂直于直径AB。当圆盘转过一角度φ时，两力所做的功为
W＝2Frφ＝Mφ
式中，M＝2Fr。
即力偶所做的功，等于力偶矩与角位移的乘积。
由上述可知，功包含了两个因素，即力和位移。若用F表示广义力，用Δ表示广义位移，则功的一般表达式为
W＝FΔ
从以上示例看出，一个广义力可以是一个力或一个力偶，其对应的广义位移是一个线位移或一个角位移。故广义力可有不同的量纲，相应的广义位移也可有不同的量纲。但在做功时广义力与广义位移的乘积却恒具有相同的量纲，即功的量纲。其常用单位为牛顿米（N·m）或千牛顿米（kN·m）。
2.实功和虚功
既然功是力与位移的乘积，根据力与位移的关系可将功分为两种情况：
（1）位移是由做功的力引起的。例如图13-5（a）所示简支梁，在静力荷载F1的作用下，当F1由零缓慢逐渐地加到其最终值时，其作用点沿F1方向产生了位移Δ11，简支梁达到平衡状态，其变形如图13-15（a）中虚线所示，力F1在位移Δ11上做了功。由于位移Δ11是由做功的力F1引起的，我们把力在自身引起的位移上所做的功称为实功。在这里，位移的表达符号出现了两个脚标，第一个脚标表示位移发生的位置，第二个脚标表示引起位移的原因。
图13-5 实功和虚功
（a）力状态；（b）位移状态
（2）位移不是由做功的力引起的，而是由其他因素引起的。若在如图13-5（a）所示简支梁的基础上，又在梁上施加另外一个静力荷载F2，梁就会达到新的平衡状态，F1的作用点沿F1方向又产生了位移Δ12，如图13-5（b）所示。力F1（此时的F1不再是静力荷载，而是一个恒力）在位移Δ12上做了功。由于位移Δ12不是F1引起的，而是由力F2所引起的，我们把力在由其他因素引起的位移上所做的功称为虚功。
“虚”字在这里并不是虚无的意思，而是强调做功的力与位移无关这一特点。在虚功中，既然做功的力和相应的位移是彼此无因果关系的两个因素，那么，可将二者看成是同一结构的两种独立无关的状态。其中，力系所属的状态称为力状态或者第一状态[图13-5（a）]，位移所属的状态称为位移状态或者第二状态[图13-5（b）]。
如果在力状态中有集中力、集中力偶、均布力和支座反力等外力，统称为广义力，用Fi表示。Δi表示与广义力Fi相应的广义位移，若用We表示外力虚功，则图13-6（a）所示的力状态在图13-6（b）所示的位移状态上所做的外力总虚功为We＝∑FiΔi。
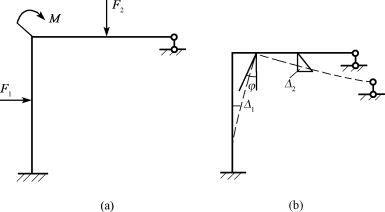
图13-6 广义力的虚功
（a）力状态；（b）位移状态
当力与位移的方向一致时，虚功为正值，当力与位移的方向相反时，虚功为负值。这里所说的虚功并非不存在，而是强调做功过程中力与位移之间彼此无因果关系。使力做虚功的位移，可以是荷载引起的位移、温度变化或支座移动等其他因素引起的位移，也可以是虚设的位移。但是上述的所有虚位移必须是约束条件所允许的微小位移。既然位移状态可以虚设，同样，力状态也可以虚设。
有关建筑力学（第2版）的文章
- 详细阅读
-
木偶表演基本功：精彩成果！详细阅读
基本功是木偶戏演员操纵木偶的基本技巧，是木偶戏演员创造人物的基本手段，也是木偶戏演员必备的条件。这二者是举偶的基本要求，是表演各种身段的基础。甩发、抖须、耍翎、摇翅等功夫，皆出自举偶，故举偶实为杖头木偶戏表演技巧之基础。由于木偶戏表演艺术特点所致，其步法更为夸张。木偶的水袖功夫木偶戏表演戏曲演员走台步，必须保持一定的重心，否则非摔跤不可。......
2023-08-16
-
鲁仲连：傲视权贵，功不受赏详细阅读
此时，鲁仲连见新坦衍，大力陈述向秦称臣的利害，令新坦衍心悦诚服，不敢再议尊秦昭王为帝的事情。鲁仲连救邯郸有功，平原君要为鲁仲连厚封土地、官爵。而鲁仲连不是个谋富贵的人，谢绝了平原君的一番好意，没有接受封地和官爵。一个月之后，就是鲁仲连的寿辰了，借此良机，等到鲁仲连喝醉的时候，平原君赏赐他千金作为寿礼。鲁仲连是齐国人，遇此大难，岂能坐视不管！田单深感鲁仲连的功劳，奏明齐君，齐侯欲封鲁仲连官爵。......
2023-11-27
-
李镇西教授详解新教师基本功详细阅读
所谓“基本功”本来特指戏曲演员应有的基础功夫，教师自然也应该有属于自己职业的基本功。根据我的教育实践，我认为，教师的基本功至少应该包括：阅读、写作、言说、思考、板书和观察。阅读，包括阅读能力和阅读习惯，这是教师的第一基本功。观察，是容易被忽视的教师基本功。......
2023-10-21
-
升降开阖功吐浊法：方法与功效详细阅读
升降开阖功吐浊法：取仰卧式姿势，然后将眼睛轻轻闭上，内视小腹丹田，以收摄杂念；次将口略向内收，形成笑容，以缓解形体和精神的紧张，使人渐入于轻松舒适的境界；同时在笑容的姿势下，舌头则会自然轻触上腭，使上下前后之阴阳，都得藉鹊桥的作用而沟通。此法升中有开，降中有合，使上下内外之阴阳，都得到相应调整，较之单行大、小周天者，功效较大。......
2024-01-08
-
徐晞功晋大司马|江阴史事纵横详细阅读
徐晞功晋大司马明代江阴出了两个兵部尚书，一个是前期承平之世的徐晞，一是后期多事之秋的刘光济，两人都有功于社稷，入祀江阴文庙乡贤祠。徐晞，字孟初，号暨阳，江阴西大街人。由此，徐晞被称为“不可先生”。徐晞经举荐到北京参与宫廷营建事务，初授工部衙门营缮司都事，督取工料木石。宣德元年徐晞调升兵部武库司郎中（正五品），执掌军队刀枪火器的供应。对如何破敌象阵，深谋远虑的徐晞已有筹划。......
2024-05-16
-
南大吉校订《传习录》，功于王学，神而明之详细阅读
因当时朝廷贬抑王学，南大吉为了“以身明道”，顶着极大压力，校订并续刻该书，颇有功于王学。习礼之日，免其课仿。量其资禀，能二百字者止可授以一百字，常使精神力量有余，则无厌苦之患，而有自得之美。“神而明之，则存乎其人”②。②神而明之，则存乎其人：出自《周易·系辞上》“神而明之，存乎其人”。每个学生务必要如实应答，有则改之，无则加勉。王阳明在本篇《教约》中规定了蒙学教学的更具体的方法。......
2023-11-21
-
何功伟：狱中的坚定决心详细阅读
何功伟又名何彬，生前任中共鄂西特委书记。当时担任第六战区司令兼湖北省主席的陈诚紧步皖南事变的后尘，一手制造了“鄂西事件”，摧毁了中共鄂西特委，逮捕了特委书记何功伟。何功伟先后被囚在恩施鼓楼街16号和方家坝看守所。此后，何功伟两次给父亲写信向父亲表明“牺牲个人，以利社会国家”的坚强决心。11月16日，敌特宣布了何功伟的死刑。17日，何功伟被杀害于方家坝监狱，时年27岁。......
2023-07-17
相关推荐