超静定结构与静定结构对比，具有以下一些重要特性。了解这些特性，有助于加深对超静定结构的认识，并更好地应用。超静定结构的这一特性，在一定条件下会带来不利影响，例如连续梁可能由于地基不均匀沉陷而产生过大的附加内力。但超静定结构的内力单由平衡条件则无法全部确定，还必须考虑变形条件才能确定其解答，因此其内力数值与材料性质和截面尺寸有关。因此，从军事及抗震方面来看，超静定结构具有较强的防御能力。......
2023-08-30
静定结构的特性分析
【摘要】：静定结构是无多余约束的几何不变体系。当由平衡力系组成的荷载作用于静定结构的某一本身为几何不变的部分上时，则只有此部分受力，其余部分的反力和内力均为零。图12-37静定结构平衡力系的影响静定结构的荷载等效性。静定结构上某一几何不变部分上的外力，当用一等效力系替换时，仅等效替换作用区段的内力发生变化，其余部分内力不变。图12-38静定结构构造变换特性
静定梁、静定刚架、静定桁架和三铰拱都属于静定结构，虽然这些结构形式各异，但都具有共同的特性：
（1）静定结构解的唯一性。静定结构是无多余约束的几何不变体系。由于没有多余约束，其所有的支座反力和内力都可以由静力平衡方程完全确定，并且解答只与荷载及结构的几何形状、尺寸有关，而与构件所用的材料、构件截面的形状和尺寸无关。
（2）静定结构只在荷载作用下产生内力。其他因素作用时（如支座移动、温度变化、制造误差等），只引起位移和变形，不产生内力。
如图12-35所示悬臂梁，若其上、下侧温度分别升高t1和t2（假设t1＜t2），则变形产生伸长和弯曲（如图12-35中虚线所示）。但因没有荷载作用，由平衡条件可知，梁的支座反力和内力均为零。又如图12-36所示简支梁，其支座B产生了塌陷，因而梁随之产生位移（如图12-36中虚线所示）。同样，由于荷载为零，其支座反力和内力也均为零。
图12-35 悬壁梁
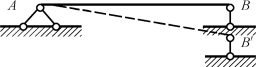
图12-36 简支梁
（3）平衡力系的影响。当由平衡力系组成的荷载作用于静定结构的某一本身为几何不变的部分上时，则只有此部分受力，其余部分的反力和内力均为零。
如图12-37所示静定结构，有平衡力系作用于本身为几何不变的部分BD上。若依次取BC、AB为隔离体计算，则可以得到支座C处的反力、支座A处的反力以及铰B处的约束力均为零，由此可知，除了BD部分外，其余部分的内力均为零。
图12-37 静定结构平衡力系的影响
（4）静定结构的荷载等效性。如果两组荷载的合力相同，则称为等效荷载。把一组荷载变换成另一组与之等效的荷载，称为荷载的等效变换。
静定结构上某一几何不变部分上的外力，当用一等效力系替换时，仅等效替换作用区段的内力发生变化，其余部分内力不变。
（5）静定结构的构造变换特性。当静定结构的一个内部几何不变部分，用其他几何不变的结构去替换时，仅被替换部分内力发生变化，其他部分的内力不变。
如图12-38（a）所示桁架中，设将上弦杆CD改为一个小桁架，如图12-38（b）所示，因两个结构的支座反力没有改变，所以除了CD杆外，其余各杆的内力均不变。
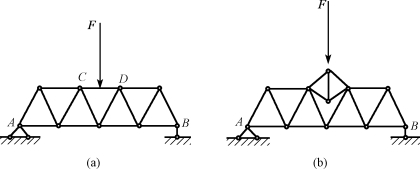
图12-38 静定结构构造变换特性
有关建筑力学（第2版）的文章
- 详细阅读
-
结构力学：静定结构特性详细阅读
主要有以下几点：1.静定结构解的唯一性静定结构是无多余约束的几何不变体系。因此，当静定结构和荷载一定时，其反力和内力的解答是唯一的确定值。图3-412.静定结构的局部平衡性静定结构在平衡力系作用下，其影响的范围只限于受该力系作用的最小几何不变部分，而不致影响到此范围以外。图3-423.静定结构的荷载等效性若两组荷载的合力相同，则称为等效荷载。......
2023-08-30
-
超静定结构的特性及优化方法详细阅读
超静定结构与静定结构相比，具有以下一些重要特性。了解这些特性，有助于加深对超静定结构的认识，并更好地应用它们。超静定结构的内力单由静力平衡条件不能全部确定，还需要同时考虑位移条件。所以，超静定结构的内力与结构的材料性质以及杆件截面尺寸有关。在超静定结构中，任何上述因素作用，通常都会引起内力。因此超静定结构比静定结构具有较强的防护突然破坏能力。在设计防护结构时，应该选择超静定结构。......
2023-06-16
- 详细阅读
-
系统稳态结构和静特性分析详细阅读
图1.30所示系统采用比例调节器，是有静差调速系统。电压反馈的极性与转速给定极性相反，因此是电压负反馈，电流反馈极性与给定极性相同，因此是正反馈。图1.31 电压负反馈电流正反馈控制直流调速系统稳态结构图将静特性[见式]与转速负反馈系统[见式]比较可以看出，电压反馈只是将电压环内电阻Rn造成的转速降减小了，而环外电阻Ra造成的转速降仍和开环调速时一样。......
2023-06-19
-
结构力学：静定和超静定平面刚架的计算方法详细阅读
杆件轴线及荷载作用线均处在同一平面内的刚架，称为平面刚架。在工程中实际应用的刚架，多数是超静定的，静定刚架较少采用。图3-112.静定平面刚架计算静定刚架的内力通常有弯矩、剪力和轴力，其计算方法原则上与静定梁的计算相同。......
2023-08-30
-
润滑结构分类及特性分析详细阅读
即使状态相同，根据负重等不同，也可将润滑结构分为边界润滑、混合润滑式和油膜润滑三种。图9-2 轴颈轴承和滑动轴承的润滑状态润滑是液体的流动，因此应符合下述牛顿黏性定律。此领域的润滑特性可以采用黏性液体相关问题，称为油膜润滑领域。边界润滑在发动机起动或停止时活塞和活塞环等发动机各部分中发生。往复式内燃机的各部件润滑在正常状态下进行油膜润滑。......
2023-06-28
-
超静定结构的概念-结构力学书详细阅读
在前面各章中，已经详细地讨论了静定结构的计算问题，静定结构的全部反力和内力可由静力平衡条件确定。超静定结构的应用范围很广，图6-1 所示为一些工程中常见的超静定结构类型。图6-1常见的超静定结构从本章开始，我们将讨论超静定结构的计算问题。按照线弹性的计算理论，超静定结构的计算方法主要有以下两种：力法。力法和位移法是超静定结构计算的基本方法。......
2023-08-30
相关推荐