应用结点法计算桁架内力时，常会遇到一些特殊的结点，可以根据节点的平衡条件判定桁架中某些杆件的轴力为零，或者可以判定与某一结点相连的两杆内力数值相等，从而使计算得以简化。截面法是用适当的截面，截取桁架中包含两个以上结点的部分为隔离体。因此，由平衡条件3.结点法和截面法的联合应用结点法和截面法是计算桁架内力......
2023-08-30
静定平面桁架内力的计算方法
【摘要】：平面汇交力系可以建立两个独立的平衡方程，解算两个未知量。继续取8、6、7等结点为隔离体，可求得桁架右半边各杆的内力。图12-30桁架轴力示意在桁架内力计算时，往往会遇到内力为零的杆件，这种杆件称为零杆。计算桁架的内力宜从几何分析入手，以便选择适当的计算方法，灵活地选取隔离体和平衡方程。除结点法外，计算桁架内力的另一基本方法是截面法。截面法适用于联合桁架的计算以及简单桁架中求少数指定杆件内力的情况。
（1）结点法。所谓结点法就是取桁架的结点为隔离体，利用结点的静力平衡条件来计算杆件内力的方法。
因为桁架各杆件都只承受轴力，作用于任一结点的各力（包括荷载、反力和杆件轴力）组成一个平面汇交力系。平面汇交力系可以建立两个独立的平衡方程，解算两个未知量。用这种方法分析桁架内力时，可首先由整体平衡条件求出它的反力，然后再以不超过两个未知力的结点分析，依次考虑各结点的平衡，直接求出各杆的内力。
计算时，通常都先假定杆件内力为拉力，若所得结果为负，则为压力。
【例12-6】试用结点法求图12-29（a）所示桁架各杆的内力。
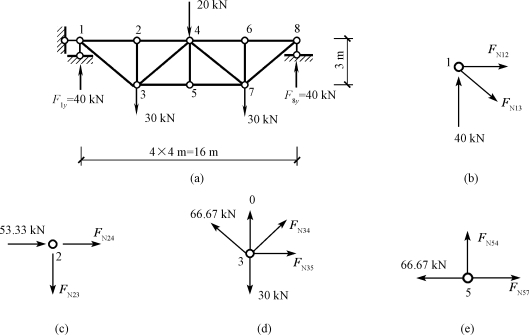
图12-29 例12-6图
解：（1）计算支座反力。由于结构和荷载均对称，故
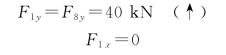
（2）计算各杆的内力。求出反力后，可截取结点解算各杆的内力。从只含两个未知力的结点开始，这里有1、8两个结点，现在计算左半桁架，从结点1开始，然后依次分析其相邻结点。
取结点1为隔离体，如图12-29（b）所示。
得
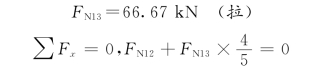
得
FN12＝－53.33kN（压）
取结点2为隔离体，如图12-29（c）所示。
得
FN24＝－53.33kN（压）
∑Fy＝0
得
FN23＝0
取结点3为隔离体，如图12-29（d）所示。
得
FN34＝－16.67kN（压）
得
FN35＝66.67kN（拉）
取结点5为隔离体，如图12-29（e）所示。
∑Fy＝0
得
FN54＝0
∑Fx＝0,FN57－66.67＝0
得
FN57＝66.67kN（拉）
至此，桁架左半边各杆的内力均已求出。继续取8、6、7等结点为隔离体，可求得桁架右半边各杆的内力。各杆的轴力示于图12-30上。由该图可以看出，对称桁架在对称荷载作用下，对称位置杆件的内力也是对称的。因此，今后在解算这类桁架时，只需计算半边桁架的内力即可。
图12-30 桁架轴力示意
在桁架内力计算时，往往会遇到内力为零的杆件，这种杆件称为零杆。如果我们在进行内力计算前根据结点平衡的一些特殊情况，将桁架中的零杆找出来，可以省去部分计算工作量。现将几种主要的特殊情况列举如下：
①不共线的两杆结点，当结点上无荷载作用时，两杆内力为零[图12-31（a）]，即F1＝F2＝0。
②由三杆构成的结点，当有两杆共线且结点上无荷载作用时[图12-31（b）]，则不共线的第三杆内力必为零，共线的两杆内力相等，符号相同，即F1＝F2，F3＝0。
③由四根杆件构成的“K”形结点，其中两杆共线，另两杆在此直线的同侧且夹角相同[图12-31（c）]，当结点上无荷载作用时，则不共线的两杆内力相等，符号相反，即F3＝－F4。
④由四根杆件构成的“X”形结点，各杆两两共线[图12-31（d）]，当结点上无荷载作用时，则共线杆件的内力相等，且符号相同，即F1＝F2，F3＝F4。
图12-31 桁架内力计算的特殊情况
⑤对称桁架在对称荷载作用下，对称杆件的轴力是相等的，即大小相等，拉压相同；在反对称荷载作用下，对称杆件的轴力是反对称的，即大小相等，拉压相反。
计算桁架的内力宜从几何分析入手，以便选择适当的计算方法，灵活地选取隔离体和平衡方程。如有零杆，先将零杆判断出来，再计算其余杆件的内力，以减少运算工作量，简化计算。
【例12-7】求图12-32所示桁架中a杆的内力（a杆与水平杆的夹角为45°）。
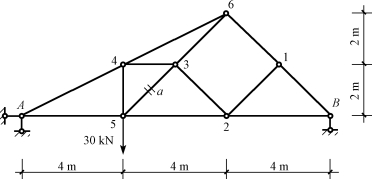
图12-32 例12-7图
解：求a杆的轴力Na时，不必求出支座反力。可以利用上述结点平衡的特殊情况，先找出零杆，然后由结点5的平衡条件直接求出该杆的轴力。依次由结点1、2、3和4可知
N12＝N23＝N34＝N45＝0
取结点5为隔离体
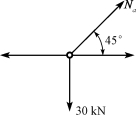
由
得
（2）截面法。除结点法外，计算桁架内力的另一基本方法是截面法。所谓截面法，是通过需求内力的杆件做一适当的截面，将桁架截为两部分，然后任取一部分为隔离体（隔离体至少包含两个结点），根据平衡条件来计算所截杆件的内力的方法。在一般情况下，作用于隔离体上的诸力（包括荷载、反力和杆件轴力）构成平面一般力系，可建立三个平衡方程。因此，只要隔离体上的未知力数目不多于三个，则可直接把此截面上的全部未知力求出。
截面法适用于联合桁架的计算以及简单桁架中求少数指定杆件内力的情况。
应用截面法时，注意以下几个方面可使计算简化。
①适当地选取截面，选取的截面可以为平面，也可以为曲面，或者为闭合截面，但一定要将桁架分成两部分。一般来说，截面所截断的杆件不多于三根。
②适当选取矩心，一般以未知内力的交点作为矩心，应用力矩方程求解内力较方便。同时，注意使用投影方程，适当选择投影轴，并将未知内力沿坐标轴分解，再利用比例关系求得内力。
【例12-8】试用截面法计算图12-33（a）所示桁架中a、b、c三杆内力。
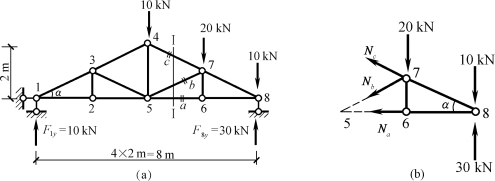
图12-33 例12-8图
解：（1）计算支座反力。
F1y＝10kN，F8y＝30kN（方向向上）
（2）求指定杆件内力。用截面Ⅰ—Ⅰ假想将a、b、c三杆截断，取截面右边部分为隔离体，如图12-33（b）所示，其中只有Na、Nb、Nc三个未知量，从而可利用隔离体的三个平衡方程求解。应用平衡方程求内力时，应注意避免解联立方程，尽量做到一个方程求解一个未知量。
∑M7＝0,－Na×1－10×2＋30×2＝0
得
Na＝40kN（拉）
∑M5＝0,Ncsinα×2＋Nccosα×1＋30×4－20×2－10×4＝0
得
Nc＝－22.36kN（压）
∑M8＝0,Nbsinα×2＋Nbcosα×1＋20×2＝0
得
Nb＝－22.36kN（压）
（3）结点法与截面法的联合应用。计算桁架时，有时联合应用结点法和截面法更为方便。关键是如何选取截面和结点。
【例12-9】试求图12-34（a）所示桁架中①、②杆的内力。
解：这是一简单桁架，用结点法可以求出全部杆件的内力，但现在只求杆①、②的内力，而用一次截面法也不能求出①、②杆的内力，所以联合应用结点法和截面法求解更为方便。
（1）求支座反力。
FAy＝FBy＝90kN
（2）求杆①、②的内力。
假想用Ⅰ—Ⅰ截面将桁架截开，取左边为隔离体，如图12-34（b）所示。由于除了N1外，其余三杆未知内力都通过D点，故用力矩方程可求得N1。
图12-34 例12-9图
∑MD＝0,6N1＋30×4＋15×8－90×8＝0
得
N1＝80kN（拉）
取结点K为隔离体，如图12-34（c）所示，该结点正好是K形结点，所以N2＝－N3。
再用Ⅱ—Ⅱ截面假想将桁架截开，以左边为隔离体，如图12-34（d）所示。
得
N2＝12.5kN（拉）
有关建筑力学（第2版）的文章
- 详细阅读
-
静定平面刚架内力计算方法详细阅读
静定平面刚架的内力计算同梁一样，仍是用截面法截取隔离体，然后用平衡条件求解。根据荷载情况，将刚架分解成若干杆段，由平衡条件求出杆端内力。该杆上作用有一集中荷载，可以分为CE和EB两个无荷载区段，用截面法求出下列控制截面的弯矩：便可以绘制出该杆弯矩图。根据荷载和已经求出的反力，可以用截面法求出杆件各个控制截面的剪力和轴力，从而绘制出整个钢架的剪力图和轴力图，如图12-18、所示。......
2023-06-16
-
静定平面刚架内力计算方法(建筑力学第3版)详细阅读
静定平面刚架的内力包括弯矩、剪力与轴力。根据前述内力图绘制法逐杆绘制刚架的内力图，并进行校核。求支座反力时要根据支座的性质定出支座反力未知量的个数，然后假定反力方向，由平衡方程确定其数值。求图13-9所示刚架的支座反力。（二）刚架杆截面内力的计算1.刚架内力正负号的规定刚架的内力有弯矩、剪力和轴力。如杆端截面C1、C2的弯矩分别用MCA、MCD表示，剪力和轴力分别用QCA、QCD和NCA、NCD表示。......
2023-08-26
-
结构力学：静定和超静定平面刚架的计算方法详细阅读
杆件轴线及荷载作用线均处在同一平面内的刚架，称为平面刚架。在工程中实际应用的刚架，多数是超静定的，静定刚架较少采用。图3-112.静定平面刚架计算静定刚架的内力通常有弯矩、剪力和轴力，其计算方法原则上与静定梁的计算相同。......
2023-08-30
-
桁架内力计算方法及应用案例详细阅读
桁架的内力计算方法有节点法、截面法、联合法。桁架中某杆的轴力为零时，此杆称为零杆。图13-16试用节点法计算图13-17所示桁架的各杆内力。求图13-19所示桁架1、2、3杆的内力N1、N2、N3。如图13-20所示，欲求图中a杆的内力，如果只用节点法计算，无论取哪个节点为隔离体，都有三个以上的未知力，无法直接求解；如果只用截面法计算，也需要解联立方程。宜联合应用节点法和截面法，求所需反力和指定杆件内力。......
2023-08-26
-
1.8.3静定桁架计算方法：完整指南详细阅读
静定桁架一般采用节点法和截面法进行内力计算。 有一钢筋混凝土非预应力屋架，如图1.8-12所示。结构设计使用年限为50年。上弦杆的计算长度可取节间长度的两倍。基本组合为由可变荷载效应控制的组合。RAv=23.4 RAv=25.2 RAv=21 RAv=19.5答案：解答：荷载设计值：1.4×P2=8.4kN图1.8-12 图2.在恒荷载和活荷载的作用下，上弦杆件S1的内力设计值与下列（ ）项数值相接近。......
2023-08-28
-
平面桁架的组成与分类详细阅读
桁架是由直杆组成，全部由铰结点连接而成的结构。图3-24图3-25在平面桁架的计算简图中，通常做如下三点假定：每个结点都是光滑无摩擦力的理想铰结点；每根杆件的轴线都是直线，且在同一平面内都通过铰的中心；所有荷载都作用在结点上。符合上述假定的桁架称为理想桁架，当桁架中各杆的轴线和外力都作用在同一平面内时，称为平面桁架。图3-26桁架的内力计算与其几何组成有着紧密的联系，按桁架几何组成的特点，平面桁架可分为：简单桁架。......
2023-08-30
-
平面任意力系的计算方法详细阅读
平面任意力系是工程实际中最常见的一种力系，工程计算中的许多实际问题都可以简化为平面任意力系问题来处理。忽略摩擦和自重，当OA 在水平位置、冲压力为F 时系统处于平衡状态。由于曲轮I 承受平面任意力系作用，利用已学过的平面汇交力系平衡和力偶系平衡方程，无法求解力偶矩M 的大小。......
2023-06-19
相关推荐