横向排架结构体系 横向平面排架由屋面梁或屋架、横向柱列和基础等组成，它是厂房的基本承重结构。其作用是保证厂房结构的纵向稳定和承重，厂房纵向排架虽承受竖向荷载，但主要承受纵向水平荷载，如纵向风荷载、吊车纵向制动力、纵向地震作用和温度应力等。......
2023-08-28
平面几何分析的组成结构
【摘要】：对一个平面体系进行几何组成分析时，其可能的最终结果共有四种情况：几何不变体系，且无多余约束；几何不变体系，且有多余约束；常变体系；瞬变体系。在进行平面体系的几何组成分析时，一定要注意每根杆件使用且只能使用一次。由三刚片规则可知，它们所组成的体系是几何不变体系，并且没有多余约束。试对图11-24所示的体系进行几何组成分析。
对一个平面体系进行几何组成分析时，其可能的最终结果共有四种情况：
（1）几何不变体系，且无多余约束；
（2）几何不变体系，且有多余约束；
（3）常变体系；
（4）瞬变体系。
其中，前两种可以作为结构使用，而后两种不能作为结构使用。
在进行平面体系的几何组成分析时，一定要注意每根杆件使用且只能使用一次。
【例11-4】试对图11-20所示的体系进行几何组成分析。
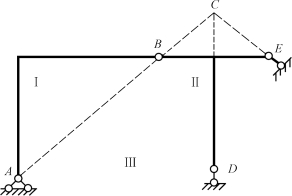
图11-20 例11-4图
解：将AB、BED和基础分别作为刚片Ⅰ、刚片Ⅱ、刚片Ⅲ。刚片Ⅰ和Ⅱ用单铰B相连；刚片Ⅰ和刚片Ⅲ用铰A相连；刚片Ⅱ和Ⅲ用虚铰C（D和E两处支座链杆的交点）相连。因A、B、C三铰在同一直线上，故该体系为瞬变体系。
【例11-5】试对图11-21（a）所示的体系进行几何组成分析。
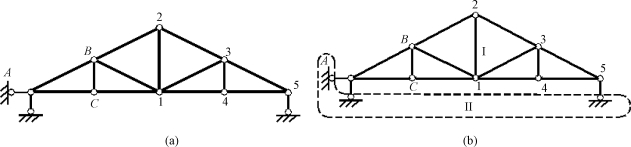
图11-21 例11-5图
解：根据三角形的稳定性可知，铰接三角形ABC是几何不变的，以铰接三角形ABC为基础，连续增加二元体B—C—1、B—1—2、1—2—3、1—3—4、3—4—5。根据二元体规则可知，上部组成无多余约束的几何不变体系，将上部几何不变体系看作一个大的刚片Ⅰ，基础看作刚片Ⅱ[图11-21（b）]，则根据两刚片规则可知，整个体系组成无多余约束的几何不变体系。
【例11-6】试对图11-22（a）所示的体系进行几何组成分析。
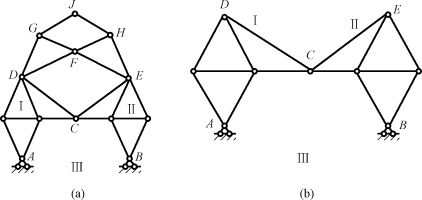
图11-22 例11-6图
解：①根据二元体规则，先依次撤除二元体G—J—H、D—G—F、F—H—E和D—F—E使体系简化，得到如图11-22（b）所示的体系。
②把任何一根杆件作为一个刚片，再通过依次增加二元体的办法，即可得到刚片ADC和CEB，并把它们记为刚片Ⅰ和刚片Ⅱ，再把基础视为刚片Ⅲ，如图11-22（b）所示。
③刚片Ⅰ和刚片Ⅱ之间由铰C连接，刚片Ⅰ和刚片Ⅲ之间由铰A相连接，刚片Ⅱ和刚片Ⅲ之间由铰B相连接，此三铰不在同一直线上。由三刚片规则可知，它们所组成的体系是几何不变体系，并且没有多余约束。
因此，如图11-22（a）所示的体系是几何不变的，并且没有多余约束。
【例11-7】试对图11-23所示的体系进行几何组成分析。
图11-23 例11-7图
解：杆AB与基础通过三根不完全平行也不汇交于一点的链杆相连（或者说杆AB与基础通过铰A和延长线不通过铰A的链杆相连），组成几何不变体系，再增加A—C—E和B—D—F两个二元体，组成了一个更大的几何不变体系。在此基础上，又增加了一根链杆CD，故此体系为具有一个多余约束的几何不变体系。
【例11-8】试对图11-24（a）所示的体系进行几何组成分析。
解：①首先，把地基及位于A处的小二元体（即固定铰支座）视为刚片Ⅰ，把铰接三角形BCE视为刚片Ⅱ，再把杆件DF视为刚片Ⅲ，如图11-24（b）所示。
②刚片Ⅱ通过链杆①和链杆AB（形成虚铰，位于C处）与刚片Ⅰ相连接；刚片Ⅲ通过链杆②和链杆AD（形成虚铰，位于F处）与刚片Ⅰ相连接；刚片Ⅱ由链杆DB和链杆FE（形成虚铰，位于G处）与刚片Ⅲ相连接。由于连接三刚片的三个单铰位于同一直线上，因此，图11-24（a）所示的体系为瞬变体系。
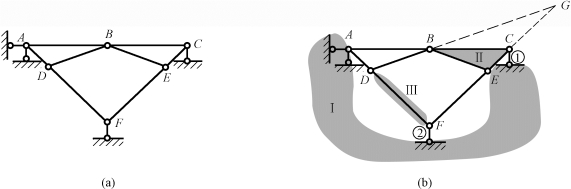
图11-24 例11-8图
从本题的分析过程中可以看到，刚片的选择至关重要，它是对结构的组成进行顺利分析的关键。
有关建筑力学（第2版）的文章
- 详细阅读
-
结构力学：平面体系几何组成分析实例详细阅读
利用组成几何不变体系的基本规则，可以组成各种各样的几何不变体系，也可以利用这些规则对已有的体系进行几何组成分析。下面将通过具体的例子来说明平面体系的几何组成分析。两刚片由铰 C 和杆 IJ 连接，根据规则 2 可知，体系为几何不变体，且无多余约束，作为一个大刚片。 试对图 2-16所示体系做几何组成分析。如果铰B 和虚铰O1、O2不在同一条直线上，则此体系为无多余约束的几何不变体系；如果此三铰在同一条直线上，则为瞬变体系。......
2023-08-30
-
佛塔结构分析：重要组成部分以及功能详细阅读
如果把一些小型的塔排除在外的话，一般古塔的主体结构可以分为四大部分。砖壁木楼层塔身，此种塔身的砖体内部好似一个空筒，因此也有称之为空筒式塔身的。中心塔柱的结构方法对于塔的稳定更为有利。砖石塔心柱塔身，这种塔身的结构是中国古代砖石结构发展到高峰的实物，在塔的主体结构上完全摆脱了以木材作为辅助构件的结构方法。塔刹作为塔的最为崇高的部分，冠盖全塔，至为重要，因此用了“刹”这个字。......
2023-12-06
-
RC的组成结构|PCIExpress体系结构详细阅读
RC是PCIe体系结构的一个重要组成部件，也是一个较为混乱的概念。RC的提出与x86处理器系统密切相关。而在图4-8中的PowerPC处理器系统中，RC的概念并不明晰。其中RCRB由一系列“管理存储器系统”的寄存器组成，而仅存在于x86处理器中；而Event Collector用来处理来自PCIe设备的错误消息报文和PME消息报文。在P4080处理器中，RC可以使用PEX_CONFIG_ADDR与PEX_CONFIG_DATA寄存器对EP进行配置读写，这两个寄存器与MPC8548处理器HOST主桥的PCI_CONFIG_ADDR和PCI_CONFIG_DATA寄存器类似，本章不再详细介绍这组寄存器。......
2023-10-20
-
伺服系统结构与组成优化详细阅读
机电一体化的伺服控制系统的结构类型繁多，但从自动控制理论的角度来分析，伺服控制系统一般包括控制器、功率放大器、执行机构、检测装置四部分。图4－4给出了伺服系统组成原理框图。①系统精度：伺服系统精度指的是输出量复现输入信号要求的精确程度，以误差的形式表现，可概括为动态误差、稳态误差和静态误差3个方面。......
2023-06-23
-
沥青混合料组成与结构详细阅读
沥青混合料主要是由粗集料、细集料、矿粉、沥青以及外加剂组成的一种复合材料，材料与级配的不同使得沥青混合料具有不同的组成结构，主要包括三种结构，即悬浮密实结构、骨架空隙结构、骨架密实结构，见图8.7。我国用量最大的AC型沥青混合料就是按照连续型密级配原理设计的、典型的悬浮密实结构。......
2023-09-01
-
温度系统的组成要点分析，详细阅读
图11-39 单回路温度控制示意图3.PID控制曲线通过调整PID参数使整个加热控制最大程度减少超调和振荡，使系统兼顾稳定性和快速性，理想的温度控制实时曲线达到如图11-40所示。......
2023-06-16
-
LED控制系统的结构和组成详细阅读
LED控制系统由控制系统和驱动系统两大部件组成。LED控制系统内置高性能单片微型控制芯片，控制器通过内部控制程序向LED驱动芯片发送控制信号和数据，LED驱动芯片根据控制信号和数据的要求，产生相应的动作，从而对每一路红、绿、蓝LED实现单独的控制。驱动系统驱动系统的功能是接收颜色数据并驱动LED按该数据所表示的亮度值显示。LED控制系统承载着控制的总功能，在LED越来越被广泛使用的今天，其功能也将越来越强大。......
2023-06-15
相关推荐