截面法确定扭矩1.扭矩图当轴上同时作用两个以上的外力偶矩时，为了形象地表示各截面扭矩的大小和正负，以便分析危险截面，常需画出扭矩随截面位置变化的图形，这种图形称为扭矩图。作扭矩图：根据上述计算结果，按比例画扭矩图[图6-10]。图6-11扭矩图的简洁画法☆想一想 练一练若两轴上的外力偶矩及各段轴长相等，而截面尺寸不同，其扭矩图相同吗？......
2023-06-19
计算外力偶矩和扭矩图方法
【摘要】：但工程上许多受扭构件，如传动轴等，往往并不直接给出其外力偶矩，而是给出轴所传递的功率和转速，这时可用下述方法计算作用于轴上的外力偶矩。现在用截面法，根据平衡方程计算各段内的扭矩。
1.外力偶矩的计算
轴扭转时的外力，通常用外力偶矩Me表示。但工程上许多受扭构件，如传动轴等，往往并不直接给出其外力偶矩，而是给出轴所传递的功率和转速，这时可用下述方法计算作用于轴上的外力偶矩。
设某轴传递的功率为Pk，转速为n，单位r/min（每分钟转速），由理论力学可知，该轴的外力偶矩Me为
式中ω为该轴的角速度（rad/s）。
若Pk的单位为千瓦（kW），则
若Pk的单位为马力（1hp＝735.5 W），则
应当指出，外界输入的主动力矩，其方向与轴的转向一致，而阻力矩的方向与轴的转向相反。
2.扭矩和扭矩图
作用在轴上的外力偶矩Me确定之后，即可用截面法研究其内力。现以图10-6（a）所示圆轴为例，假想地将圆轴沿n—n截面分成左、右两部分，保留左部分作为研究对象，如图10-6（b）所示。由于整个轴是平衡的，所以左部分也处于平衡状态，这就要求截面n—n上的内力系必须归结为一个内力偶矩T，且由左部分的平衡方程
T－Me＝0
得
T＝Me
力偶矩T称为截面n—n上的扭矩，是左、右两部分在n—n截面上相互作用的分布内力系的合力偶矩。扭矩的符号规定如下：若按右手螺旋法则，把T表示为双矢量，当双矢量方向与截面的外法线方向一致时，T为正，反之为负（图10-7）。按照这一符号规定，图10-6（b）所示扭矩T的符号为正。当保留右部分时[图10-6（c）]，所得扭矩的大小、符号将与按保留左部分计算结果相同。
图10-6 扭矩和扭矩图
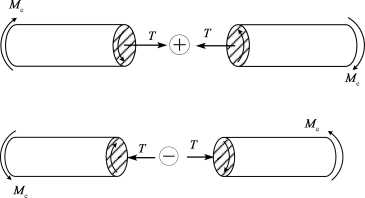
图10-7 扭矩的正负号规定
若作用于轴上的外力偶多于两个，也与拉伸（压缩）问题中画轴力图一样，往往用图线来表示各横截面上的扭矩沿轴线变化的情况。图中以横轴表示横截面的位置，纵轴表示相应横截面上的扭矩。这种图线称为扭矩图。图10-6（d）为图10-6（a）所示受扭圆轴的扭矩图。
【例10-4】传动轴如图10-8（a）所示，主动轮A输入功率PA＝50hp，从动轮B、C、D输出功率分别为PB＝PC＝15hp，PD＝20hp，轴的转速为n＝300r/min，试画出轴的扭矩图。
解：按式（10-5）计算出作用于各轮上的外力偶矩
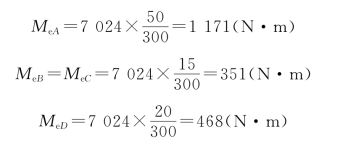
从受力情况看出，轴在BC、CA、AD三段内，各截面上的扭矩是不相等的。现在用截面法，根据平衡方程计算各段内的扭矩。
在BC段内，以T1表示1—1截面上的扭矩，并假设T1的方向为正向，如图10-8（b）所示。由平衡方程
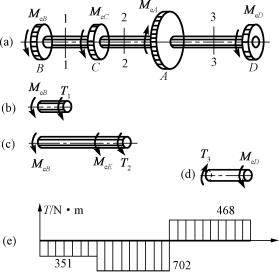
图10-8 例10-4图
T1＋MeB＝0
得
T1＝－MeB＝－351(N·m)
等号右边的负号说明，在图10-8（b）中对T1所假定的方向与1—1截面上的实际扭矩方向相反。在BC段内，各截面上的扭矩不变，均为－351N·m。所以在这一段内扭矩图为一水平线，如图10-8（e）所示。在CA段内，由图10-8（c），得
T2＋MeC＋MeB＝0
T2＝－MeC－MeB＝－702(N·m)
在AD段内，由图10-8（d），得
T3－MeD＝0
T3＝MeD＝468(N·m)
根据所得数据，把各截面上的扭矩沿轴线变化的情况，用图表示出来，就是扭矩图[图10-8（e）]。从图中看出，最大扭矩发生于CA段内，且Tmax＝702N·m。
对于同一根轴，若把主动轮A安置于轴的一端，例如放在右端，则轴的扭矩图将如图10-9所示。这时，轴的最大扭矩Tmax＝1170N·m。可见，传动轴上主动轮和从动轮安置的位置不同，轴所承受的最大扭矩也就不同。两者相比，显然图10-8所示布局比较合理。
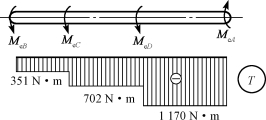
图10-9 主动轮位置改变后的扭矩图
有关建筑力学（第2版）的文章
- 详细阅读
-
如何判定扭转切应力和扭矩方向是否一致？求解各详细阅读
6-1 扭转切应力与扭矩方向是否一致？判定如图6-23 所示的切应力分布图哪些是正确的，哪些是错误的。图6-23题6-1图6-2 如图6-24 所示，试求各杆在1-1、2-2 截面上的扭矩，并作出各杆的扭矩图。图6-26图6-4图6-5 已知圆轴受外力偶矩m=2 kN·m 作用，材料的许用切应力[τ]=60 MPa。图6-28题6-8图图6-29题6-9图......
2023-06-19
-
ADAMS车辆工程案例仿真的阶跃扭矩结果图详细阅读
图6-24传动轴子系统建立图6-25传动轴子系统传动轴测试平台。图6-28扭矩输入图6-29左右限滑差速器扭矩图6-30前差速器壳bushing_1衬套X/Y/Z方向受力图6-31前差速器壳bushing_2衬套X/Y/Z方向受力图6-32前差速器壳bushing_3衬套X/Y/Z方向受力图6-33支撑轴承X/Y/Z方向受力图6-34传动轴X方向位移图6-35传动轴Y方向位移图6-36传动轴Z方向位移图6-37传动轴X方向速度图6-38传动轴Y方向速度图6-39传动轴Z方向速度......
2023-09-17
-
外圆磨削方法详解详细阅读
图11-8 纵向磨削法2)由于背吃刀量较小，工作台往复时间长，故生产率较低。纵向磨削法的磨削用量1)背吃刀量ap:粗磨:ap＝0.01～0.04mm；精磨:ap≤0.01mm。表11-2 外圆磨削用量表11-3 粗磨背吃刀量2.切入磨削法切入磨削法又称横向磨削法，如图11-9所示。2)磨削时，会产生较大的磨削力和磨削热，工件易产生变形，严重时会发生烧伤现象。图11-10 分段磨削法4.深切缓进磨削法深切缓进磨削法是一种高效率的磨削法，在一次纵向进给中将工件的全部磨削余量切除。......
2023-06-28
-
计算方法和步骤详解详细阅读
电流密度J的分布情况通过求解公式（6-1）来获得。在本节中，动静导电杆的材料采用铜，动静触头的材料采用银，电弧的电导率为银的10-4。在ANSYS有限元软件中进行静态传导电流分析，需要经过单元类型选择、定义材质属性、分配材质属性、几何模型剖分、定义边界条件、加载激励和结果处理这几个步骤。将上一步所得电流密度分布情况作为激励加载至模型上，通过有限元分析计算，可以得到灭弧室内的空间磁场分布。......
2023-06-15
-
计算直线和圆弧的方法详细阅读
图6.4-2 直线的辅助计算直线终点的定义方法、输入内容、操作步骤和点计算相同，角度的计算方法如下。在轮廓输入页面，选择〖ARC〗（顺时针）或〖ARC〗（逆时针）后，按〖AUX〗键可显示图6.4-3所示的圆弧计算页面。图6.4-3 圆弧的辅助计算该页面的功能键〖CIRCLE〗用于圆弧定义，〖ENDPNT〗、〖CENTER〗分别用于终点、圆心的计算。......
2023-06-25
-
创建工程图的步骤和方法详细阅读
图6-69创建视图的工具栏1.基础视图基础视图是不受任何约束的独立视图。利用“投影视图”命令可以创建多个视图，所创建视图与基础视图对齐，符合投影关系，并且继承基础视图的比例和显示方式。图6-77局部剖视图图6-78半剖视图4.断面图Inventor创建断面图的方法不太好理解，下面打开轴零件的三轴模型介绍创建断面图的方法。......
2023-06-28
-
ΔA和ΔG的计算方法详细阅读
但二者的变化值ΔA和ΔG都是可以求出的。现在介绍从定义式出发计算ΔA和ΔG。对于不可逆相变时ΔA和ΔG的计算，根据状态函数原理，可以在相同的始、终态之间设计另一条可逆途径，则可逆途径的ΔA和ΔG即为原过程的ΔA和ΔG。......
2023-11-23
相关推荐