首页理论教育惯性矩、惯性积与惯性半径

惯性矩、惯性积与惯性半径

2025-09-29 理论教育版权反馈

【摘要】：如图7-12所示，任意平面图形上所有微面积dA与其坐标z、y乘积的总和，称为该平面图形对z、y两轴的惯性积，用Izy表示，即图7-12平面图形对z、y轴的惯性积惯性积可为正，可为负，也可为零。可以证明，在两正交坐标轴中，只要z、y轴之一为平面图形的对称轴，则平面图形对z、y轴的惯性积就一定等于零。图7-13简单图形的惯性矩及惯性半径②简单图形的惯性半径。

1.惯性矩、惯性积、惯性半径的定义

（1）惯性矩。如图7-12所示，任意平面图形上所有微面积dA与其坐标y（或z）平方乘积的总和，称为该平面图形对z轴（或y轴）的惯性矩，用Iz（或Iy）表示，即

pagenumber_ebook=89,pagenumber_book=80

式（7-8）表明，惯性矩恒为正值。常用单位为m4或mm4。

（2）惯性积。如图7-12所示，任意平面图形上所有微面积dA与其坐标z、y乘积的总和，称为该平面图形对z、y两轴的惯性积，用Izy表示，即

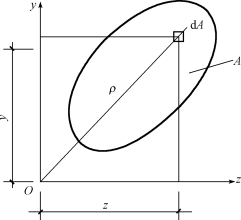
pagenumber_ebook=90,pagenumber_book=81

pagenumber_ebook=90,pagenumber_book=81

图7-12　平面图形对z、y轴的惯性积

惯性积可为正，可为负，也可为零。常用单位为m4或mm4。可以证明，在两正交坐标轴中，只要z、y轴之一为平面图形的对称轴，则平面图形对z、y轴的惯性积就一定等于零。

（3）惯性半径。在工程中，为了计算方便，将图形的惯性矩表示为图形面积A与某一长度平方的乘积，即

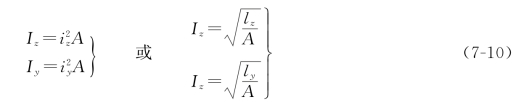
pagenumber_ebook=90,pagenumber_book=81

式中 iz、iy——平面图形对z、y轴的惯性半径，常用单位为m或mm。

（4）简单图形（图7-13）的惯性矩及惯性半径。

①简单图形对形心轴的惯性矩[由式（7-8）积分可得]。

矩形

圆形

环形

型钢的惯性矩可直接由型钢表查得。

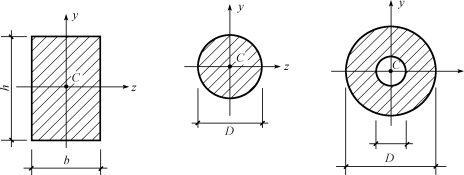
pagenumber_ebook=90,pagenumber_book=81

图7-13　简单图形的惯性矩及惯性半径

②简单图形的惯性半径。

矩形

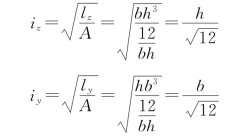pagenumber_ebook=91,pagenumber_book=82 (https://www.chuimin.cn)

圆形

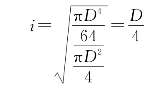
pagenumber_ebook=91,pagenumber_book=82

2.平行移轴公式

（1）惯性矩的平行移轴公式。同一平面图形对不同坐标轴的惯性矩是不相同的，但它们之间存在着一定的关系。现给出图7-14所示平面图形对两个相平行的坐标轴的惯性矩之间的关系。

pagenumber_ebook=91,pagenumber_book=82

式（7-11）称为惯性矩的平行移轴公式。它表明平面图形对任一轴的惯性矩，等于平面图形对与该轴平行的形心轴的惯性矩再加上其面积与两轴间距离平方的乘积。在所有平行轴中，平面图形对形心轴的惯性矩为最小。

（2）组合截面惯性矩的计算。组合图形对某轴的惯性矩，等于组成组合图形的各简单图形对同一轴的惯性矩之和。

【例7-5】计算图7-15所示T形截面对形心轴z的惯性矩IzC。

解：（1）求截面相对底边的形心坐标。

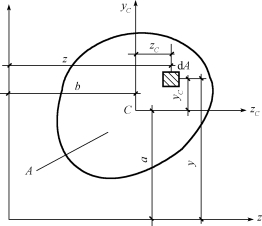
pagenumber_ebook=91,pagenumber_book=82

pagenumber_ebook=91,pagenumber_book=82

图7-14　惯性矩平行移轴

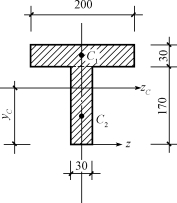
pagenumber_ebook=91,pagenumber_book=82

图7-15　例7-5图

（2）求截面对形心轴的惯性矩。

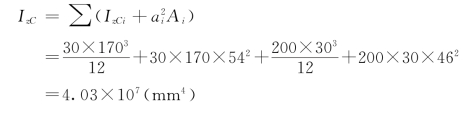
pagenumber_ebook=91,pagenumber_book=82

【例7-6】试计算图7-16所示由两根20槽钢组成的截面对形心轴z、y的惯性矩。

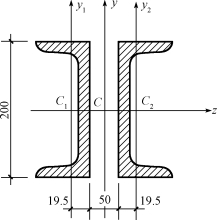
pagenumber_ebook=92,pagenumber_book=83

图7-16　例7-6图

解：组合截面有两根对称轴，形心C就在这两对称轴的交点。由型钢表查得每根槽钢的形心C1或C2到腹板边缘的距离为19.5mm，每根槽钢截面积为

A1＝A2＝3.283×103mm2

每根槽钢对本身形心轴的惯性矩为

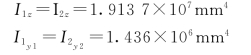
pagenumber_ebook=92,pagenumber_book=83

整个截面对形心轴的惯性矩应等于两根槽钢对形心轴的惯性矩之和，故得

pagenumber_ebook=92,pagenumber_book=83