滞后-超前校正环节的传递函数为:滞后-超前校正环节的伯德图如图12-12所示。低频段具有负的斜率和负的相位差,起滞后校正作用。图12-12 滞后-超前校正环节的伯德图图12-13 原系统的开环伯德图1.校正原理低频部分利用校正环节的滞后部分以改善系统的稳态精度。由此即可确定总的滞后-超前校正环节。......
2025-09-29
1.重心
地球上的任何物体都受到地球引力的作用,这个力称为物体的重力。可将物体看作是由许多微小部分组成,每一微小部分都受到地球引力的作用,这些引力汇交于地球中心。但是,由于一般物体的尺寸比地球的半径小得多,因此,这些引力近似地看成是空间平行力系。这些平行力系的合力就是物体的重力。由试验可知,不论物体在空间的方位如何,物体重力的作用线始终是通过一个确定的点,这个点就是物体重力的作用点,称为物体的重心。
(1)一般物体重心的坐标公式。如图7-4所示,为确定物体重心的位置,将它分割成各个微小块,各微小块重力分别为G1,G2,…,Gn,其作用点的坐标分别为(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn),各微小块所受重力的合力W即为整个物体所受的重力![]() 其作用点的坐标为C(xC,yC,zC)。对y轴应用合力矩定理,有
其作用点的坐标为C(xC,yC,zC)。对y轴应用合力矩定理,有
![]()
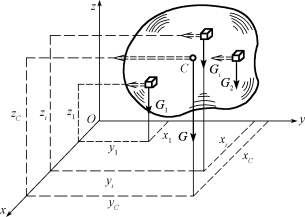
图7-4 物体重心
得
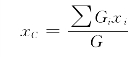
同理,对x轴取矩可得
![]()
将物体连同坐标转90°而使坐标面Oxz成为水平面,再对z轴应用合力矩定理,可得
![]()
因此,一般物体的重心坐标的公式为
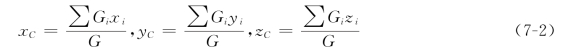
(2)均质物体重心的坐标公式。对均质物体用r表示单位体积的重力,体积为V,则物体的重力G=Vr,微小体积为Vi,微小体积重力Gi=Viy,代入式(7-2),得均质物体的重心坐标公式为

由上式可知,均质物体的重心与重力无关。因此,均质物体的重心就是其几何中心,称为形心。对均质物体来说重心和形心是重合的。
(3)均质薄板重心(形心)的坐标公式。对于均质等厚的薄平板,如图7-5所示,取对称面为坐标面Oyz,用δ表示其厚度,Ai表示微体积的面积,将微体积Vi=δAi及V=δA代入式(7-3),得重心(形心)坐标公式为
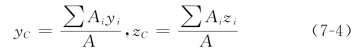
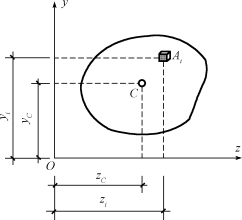
图7-5 均质等厚薄平板重心(https://www.chuimin.cn)
因每一微小部分的xi为零,所以xi=0。
2.形心
形心就是物体的几何中心。因此,当平面图形具有对称轴或对称中心时,则形心一定在对称轴或对称中心上,如图7-6所示。若平面图形是一个组合平面图形,则可先将其分割为若干个简单图形,然后可按式(7-3)求得其形心的坐标,这时公式中的Ai为所分割的简单图形的面积,而yi、zi为其相应的形心坐标,这种方法称为分割法。另外,有些组合图形,可以看成是从某个简单图形中挖去一个或几个简单图形而成,如果将挖去的面积用负面积表示,则仍可应用分割法求其形心坐标,这种方法又称为负面积法。
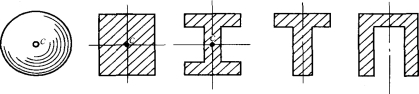
图7-6 平面图形形心位置确定
【例7-2】试求图7-7所示T形截面的形心坐标。
解:将平面图形分割为两个矩形,如图7-7所示,每个矩形的面积及形心坐标为
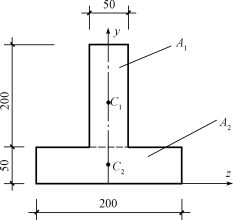
图7-7 例7-2图
A1=200×50,z1=0,y1=150
A2=200×50,z2=0,y2=25
由式(7-4)可求得T形截面的形心坐标为

【例7-3】试求图7-8所示阴影部分平面图形的形心坐标。
解:将平面图形分割为两个圆,如图7-8所示,每个圆的面积及形心坐标为
A1=π·R2,z1=0,y1=0
A2=-π·r2,z2=R/2,y2=0
由式(7-3)可求得阴影部分平面图形的形心坐标为

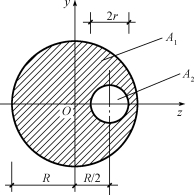
图7-8 例7-3图
相关文章

滞后-超前校正环节的传递函数为:滞后-超前校正环节的伯德图如图12-12所示。低频段具有负的斜率和负的相位差,起滞后校正作用。图12-12 滞后-超前校正环节的伯德图图12-13 原系统的开环伯德图1.校正原理低频部分利用校正环节的滞后部分以改善系统的稳态精度。由此即可确定总的滞后-超前校正环节。......
2025-09-29

图3.28由特殊塑料材质制成的特定手指机械手具有不分离的有效表面的优点是,即使使用搬运系统搬运不同的工件,也只需要接近一个夹紧点。图3.31连杆抓取机械手(8工位)和长的机械手手指特殊成型的硬质合金刀片可用于非敏感元件或对表面质量没有更严格要求的元件。图3.32被搬运的工件——单连杆图3.33在屈服强度内对机械手手指进行设计5年前,生产机械手仍然是一项昂贵且耗时的工作。......
2025-09-29

当焊缝冷却后收缩,由于受到接头周围金属的限制,而不能自由收缩时受到拉伸,产生拉应力,即焊接残余应力。控制焊接残余应力的主要方法如下:1.机械拉伸法焊后对焊接构件进行加载,使焊接接头中的不协调应变区进行拉伸到屈服,从而减少由焊接引起的拉伸残余应力,使内应力有所降低。......
2025-09-29

(一)形态设计方法在智能家电产品形态设计中,基础立体造型的创造是有规律的,这一过程和自然界中的形态构成有异曲同工之处。设计师大量运用自然界中的自然形态,将他们组合、分割或采用其他方法创造性地用于家电产品的设计之中,起到非常好的效果。有的设计师从蜂巢的结构中获取灵感,将其中最科学、最本质的方面抽取出来,用于家电产品的设计。人类社会的总体发展是向自然学习的过程,家电产品的设计也不例外。......
2025-09-29

原则上,每个自动化工序都有不同的精度要求。在这种情况下,工件位置不再精确地集中在手指之间,这可能导致连接操作中的精度问题。由于对抓取或放置精度的要求如此之高,因此应相应地调整一般条件,以避免此类错误。图3.117用公差角度来审视系统对于抓取或者放置来说十分重要摄像机测量误差可能具有不同的性质。当涉及在装配过程中对工件的纯搬运时,或如图3.117所示,当相当多的因素影响精度时,这些考虑尤其重要。......
2025-09-29

电磁场中有电路和磁路的概念,热场中也有热路的概念。从这点上讲,把热场简化为热路,其精度比电磁场简化电路和磁路的要低,但通过适当处理也可满足工程计算要求。图5-2 电路与类比的热路a)电路 b)热路表5-1 热路参数与电路参数的类比利用以上热路和电路相似原理可对一具体开关电器建立其热路网络模型,求解热网络问题可采用电网络方法求解,例如用电网络的软件PSpice来计算。另一种求解热网络方法是热网络有限差分法。......
2025-09-29

光强I光源在某一给定方向的单位立体角内发射的光通量称为光源在该方向的发光强度,简称光强。为了对光源的显色性进行定量,引入显色指数的概念。以标准光源为准,将其显色指数定为100,其余光源的显色指数均低于100。灯具效率是指在规定条件下测得的灯具所发射的光通量值与灯具内所有光源发出的光通量测定值之和的比值。......
2025-09-29
相关推荐