根据上述微分关系,可以得到下述推论,这些推论对正确绘制或校核剪力图和弯矩图有很大的帮助。因此,对于受均布载荷作用的一段梁上,其剪力图为一倾斜直线,而弯矩图为抛物线。在集中力作用截面的左、右两侧,剪力FQ 有一突然变化,弯矩图的斜率也发生突然变化,成为一个折点。表7-1梁的剪力图和弯矩图的规律案例7-5 外伸梁及其所受载荷如图7-16所示,试作梁的剪力图和弯矩图。......
2023-06-19
在[例6-8]中,若将M(x)的表达式对x取导数,就得到剪力FQ(x)。若再将FQ(x)的表达式对x取导数,则得到载荷集度q。这里所得到的结果,并不是偶然的。实际上,在载荷集度、剪力和弯矩之间存在着普遍的微分关系。现从一般情况出发加以论证。
如图6-24(a)所示为简支梁受载荷作用,其中有载荷集度为q(x)的分布载荷。q(x)是x的连续函数,规定向上为正,选取坐标系如图6-24(a)所示。若用坐标为x和x+dx的两个相邻横截面,从梁中取出长为dx的一段来研究,由于dx是微量,微段上的载荷集度q(x)可视为均布载荷,如图6-24(b)所示。
设坐标为x的横截面上的内力为FQ(x)和M(x),在坐标为x+dx的横截面上的内力为FQ(x)+dFQ(x)和M(x)+dM(x)。假设这些内力均为正值,且在dx微段内没有集中力和集中力偶。微段梁在上述各力作用下处于平衡。根据平衡条件![]() 得
得
FQ(x)-[FQ(x)+dFQ(x)]+q(x)dx=0
由此导出
![]()
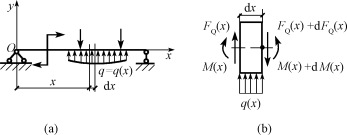
图6-24 简支梁受力图
设坐标为x+dx截面与梁轴线交点为C,由![]() 得
得
![]()
略去二阶微量![]() 可得
可得
![]()
将式(6-2)对x求一阶导数,并利用式(6-1),得

式(6-1)~式(6-3)就是载荷集度q(x)、剪力FQ(x)和弯矩M(x)之间的微分关系。它表示:
(1)横截面的剪力对x的一阶导数,等于梁在该截面的载荷集度,即剪力图上某点切线的斜率等于该点相应横截面上的载荷集度。
(2)横截面的弯矩对x的一阶导数,等于该截面上的剪力,即弯矩图上某点切线的斜率等于该点相应横截面上的剪力。
(3)横截面的弯矩对x的二阶导数,等于梁在该截面的载荷集度q(x)。由此表明弯矩图的变化形式与载荷集度q(x)的正负值有关。若q(x)方向向下(负值),即![]()
![]() ,弯矩图为向上凸曲线;反之,q(x)方向向上(正值),则弯矩图为向下凸曲线。
,弯矩图为向上凸曲线;反之,q(x)方向向上(正值),则弯矩图为向下凸曲线。
根据微分关系,还可以看出剪力和弯矩有以下规律:
(1)梁的某一段内无载荷作用,即q(x)=0,由![]() 可知,FQ(x)=常量。
可知,FQ(x)=常量。
若FQ(x)=0,剪力图为沿x轴的直线,并由![]() 可知,M(x)=常量,弯矩图为平行于x轴的直线。
可知,M(x)=常量,弯矩图为平行于x轴的直线。
若FQ(x)等于常数,剪力图为平行于x轴的直线,弯矩图为向上或向下倾斜的直线。
(2)梁的某一段内有均布载荷作用,即q(x)等于常数,则剪力FQ(x)是x的一次函数,弯矩M(x)是x的二次函数。剪力图为斜直线;若q(x)为正值,斜线向上倾斜;若q(x)为负值,斜线向下倾斜。弯矩图为二次抛物线,当q(x)为正值,即![]() 时,弯矩图为下凸曲线;当q(x)为负值,即
时,弯矩图为下凸曲线;当q(x)为负值,即![]() 时,弯矩图为上凸曲线。
时,弯矩图为上凸曲线。
(3)在集中力偶作用处,剪力图发生突变,突变的绝对值等于该集中力的数值。此处弯矩图由于切线斜率突变而发生转折。
(4)在集中力偶作用处,剪力图不受影响,而弯矩图发生突变,突变的绝对值等于该集中力偶的数值。
上述结论可用表6-1表示。
表6-1 梁上荷载和剪力图、弯矩图的关系

利用梁的剪力图、弯矩图与荷载之间的规律作梁的内力图,通常称为简捷法作剪力图、弯矩图。同时,还可以用这些规律来校核剪力图和弯矩图的正确性,避免作图时出现的错误。用简捷法作剪力图和弯矩图的步骤如下:
(1)求支座反力。对于悬臂梁由于其一端为自由端,所以可以不求支座反力。
(2)将梁进行分段。梁的端截面、集中力、集中力偶的作用截面、分布荷载的起止截面都是梁分段时的界线截面。
(3)由各梁段上的荷载情况,根据规律确定其对应的剪力图和弯矩图的形状。
(4)确定控制截面,求控制截面的剪力值、弯矩值,并作图。
控制截面是指对内力图形能起控制作用的截面。当图形为平行直线时,只要确定一个截面的内力数值就能作出图来,此时找到一个控制截面就行了;当图形为斜直线时就需要确定两个截面的内力数值才能作出图来,此时要找到两个控制截面;而当图形为抛物线时就需要至少确定三个截面的内力数值才能作出图来,此时至少要找到三个控制截面;一般情况下,选梁段的界线截面、剪力等于零的截面、跨中截面为控制截面。
【例6-10】用简捷法作图6-25(a)所示外伸梁的剪力图和弯矩图。

图6-25 例6-10图
解:(1)求支座反力。
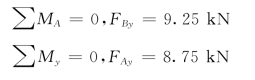
(2)将梁进行分段。根据梁上的外力情况将梁分成三段:CA段、AB段、BD段。
(3)由各梁段上的荷载情况,根据规律确定其对应的剪力图和弯矩图的形状,见表6-2。
表6-2 剪力图与弯矩图的形状

(4)确定控制截面,求控制截面的剪力值、弯矩值,并作图。水平直线确定一个控制截面即可;斜直线确定两个控制截面;抛物线至少确定三个控制截面,见表6-3。
表6-3 控制截面值
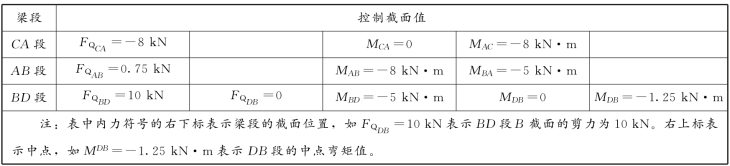
为了使作出的剪力图和弯矩图准确,通常边作图边用剪力图和弯矩图的特征(表6-1)检查图形是否正确。
作出的剪力图和弯矩图如图6-25(b)、(c)所示。
【例6-11】用简捷法作图6-26(a)所示外伸梁的剪力图和弯矩图。已知:M=12kN·m,q=2kN/m。

图6-26 例6-11图
解:(1)求支座反力。
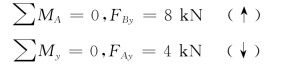
(2)将梁进行分段。
(3)由各梁段上的荷载情况,根据规律确定其对应的剪力图和弯矩图的形状,见表6-4。
表6-4 剪力图与弯矩图的形状

(4)确定控制截面,求控制截面的剪力值、弯矩值,见表6-5,并作图。
表6-5 控制截面值

作出的剪力图和弯矩图如图6-26(b)、(c)所示。
【例6-12】用简捷法作图6-27(a)所示简支梁的剪力图和弯矩图。

图6-27 简支梁受力
已知:q=40kN/m,FP=80kN,M=160kN·m。
解:(1)求支座反力。
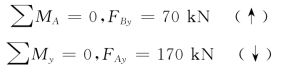
(2)将梁进行分段。
(3)由各梁段上的荷载情况,根据规律确定其对应的剪力图和弯矩图的形状,见表6-6。
表6-6 剪力图与弯矩图的形状

(4)确定控制截面,求控制截面的剪力值、弯矩值,见表6-7,并作图。
表6-7 控制截面值
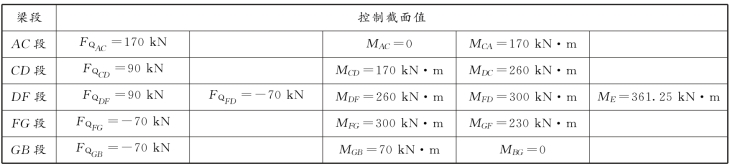
作出的剪力图和弯矩图如图6-27(b)、(c)所示。
有关建筑力学(第2版)的文章

根据上述微分关系,可以得到下述推论,这些推论对正确绘制或校核剪力图和弯矩图有很大的帮助。因此,对于受均布载荷作用的一段梁上,其剪力图为一倾斜直线,而弯矩图为抛物线。在集中力作用截面的左、右两侧,剪力FQ 有一突然变化,弯矩图的斜率也发生突然变化,成为一个折点。表7-1梁的剪力图和弯矩图的规律案例7-5 外伸梁及其所受载荷如图7-16所示,试作梁的剪力图和弯矩图。......
2023-06-19

由上面的例子可以总结出计算梁的剪力和弯矩的具体方法:剪力FQ=截面一侧所有外力的代数和,外力的正负号规定可简记为“左上右下,剪力为正”。试求指定截面上的剪力和弯矩。弯矩的突变值等于集中力偶的力偶矩的大小。因此,应用截面法计算任意截面的弯矩时,截面不能选取在集中力偶作用的截面上。......
2023-06-19

以平行于梁轴的横坐标x 表示横截面的位置,以纵坐标表示相应横截面上的剪力和弯矩,绘出剪力方程和弯矩方程的图线,这样的图线分别称为剪力图和弯矩图。作剪力图和弯矩图。试列出此梁的剪力方程和弯矩方程,并绘制剪力图和弯矩图。得图7-14均布载荷作用的简支梁列剪力方程和弯矩方程。由剪力图和弯矩图可以看出,梁上有均布载荷作用处,剪力图为斜直线,弯矩图为一段抛物线,且在剪力等于零的截面具有最大弯矩值。......
2023-06-19

6.连系梁连系梁是厂房纵向柱列的水平连系构件,用以增加厂房的纵向刚度,承受风荷载或上部墙体的荷载,并将荷载传给纵向柱列。图4-3为各承重构件的荷载传递关系。......
2023-08-20

为了对联肢剪力墙的性能有深入的理解,首先介绍由连续化方法得到的联肢剪力墙的一些弹性内力计算公式,通过计算分析了解联肢剪力墙的主要规律。图7-12 倒三角分布荷载下k—α—ξ曲线族图7-13 连杆连接的独立墙肢整体系数α是联肢剪力墙的一个重要几何参数,整体系数α表示连梁与墙肢的相对刚度。整体系数α不仅与墙肢内力分布有关,它对连梁内力分布也有很大影响。......
2023-08-23

为了形象地表明沿梁轴线各横截面上剪力和弯矩的变化情况,通常将剪力和弯矩在全梁范围内变化的规律用图形来表示,这种图形称为剪力图和弯矩图。对于非水平梁而言,剪力图可以作在梁轴线的任一侧,并标明正、负号;弯矩图作在梁受拉的一侧。根据剪力方程和弯矩方程判断剪力图和弯矩图的形状,确定控制截面的个数及内力值,作图。在集中力偶作用处,剪力图无变化,弯矩图不连续,发生突变,突变的绝对值等于集中力偶的力偶矩数值。......
2023-06-16

从孟子的论述以及朱熹的注释来看,人性必须具备以下四个要件。孟子师生与告子等人辩论的一个焦点是内在与外在。而孟子师生的反驳,则是捍卫仁义对于人的内在性。因为内在意味着先天性,一旦仁义被证明不是与生俱来的,人性善就不能成立,所以告子等人一定要挖掉这个墙脚。朱熹认为,正是这种自然之势表达本性。人性是自然而然的。相反,孟子的性善主张则符合所有四条。......
2023-10-22

不仅如此,直觉加工的快速性和即时性使得个体在紧迫的情境下能够快速整合周围环境的信息与已有经验,摆脱对认知资源的依赖,及时做出决策。不过,传统研究往往将分析加工与直觉加工视作两个独立的加工系统。现有研究指出,两者可能处于不断的相互转换之中。下面,本章将从直觉加工及分析加工的关系入手揭示两种加工过程的内在特征,并在此基础上探讨如何构建直觉。......
2023-11-01
相关推荐