时间序列预测法用于短期预测的精确度最高，中期预测其次，长期预测最低。②时间序列预测法的本质是一种统计定量分析方法。时间序列预测法是以平均数为基础的一种预测法。因果分析预测法是另一种定量预测方法，它是指利用系统内部发展因素的因果关系来预测系统发展趋势。......
2023-07-15
虎克定律及其应用于砖柱的分析
【摘要】：E的数值随材料而异，是通过试验测定的，其单位与应力单位相同。将式（5-1）及式（5-2）等代入式（5-5）可得式（5-6）是虎克定律的另一表达形式，它表明当杆件应力不超过某一极限时，应力与应变成正比。解：当P达到15kN时，正应力为由虎克定律得图5-12所示为一方形截面砖柱，上段柱边长为240mm，下段柱边长为370mm。
对于工程上常用的材料，如低碳钢、合金钢等所制成的轴向拉（压）杆，由实验证明：当杆的应力未超过某一极限时，纵向变形Δl与外力P、杆长l及横截面面积A之间存在如下比例关系：
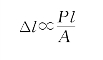
引入比例常数E，则有
在内力不变的杆段中N＝P，可将上式改写成
这一比例关系，是1678年首先由英国科学家虎克提出的，故称为虎克定律。式中比例常数E称为弹性模量，从式（5-5）知，当其他条件相同时，材料的弹性模量越大，则变形越小，它表示材料抵抗弹性变形的能力。E的数值随材料而异，是通过试验测定的，其单位与应力单位相同。EA称为杆件的抗拉（压）刚度，对于长度相等，且受力相同的拉杆，其抗拉（压）刚度越大，则变形就越小。
将式（5-1）及式（5-2）等代入式（5-5）可得
式（5-6）是虎克定律的另一表达形式，它表明当杆件应力不超过某一极限时，应力与应变成正比。
上述的应力极限值，称为材料的比例极限，用σP表示。
【例5-4】为了测定钢材的弹性模量E，将钢材加工成直径d＝10mm的试件，放在试验机上拉伸，当拉力P达到15kN时，测得纵向线应变ε＝0.00096，求这一钢材的弹性模量。
解：当P达到15kN时，正应力为
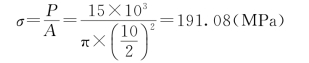
由虎克定律得
【例5-5】图5-12所示为一方形截面砖柱，上段柱边长为240mm，下段柱边长为370mm。荷载F＝40kN，不计自重，材料的弹性模量E＝0.03×105 MPa，试求砖柱顶面A的位移。
解：绘出砖柱的轴力图，如图5-12（b）所示，设砖柱顶面A下降的位移为Δl，显然它的位移就等于全柱的总缩短量。由于上、下两段柱的截面面积及轴力都不相等，故应分别求出两段柱的变形，然后求其总和，即
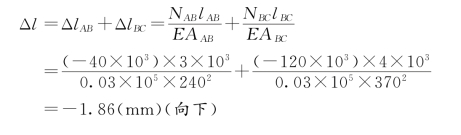
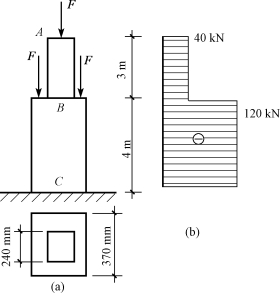
图5-12 例5-5图
【例5-6】计算图示5-13（a）结构杆①及杆②的变形。已知杆①为钢杆，A1＝8cm2，E1＝200GPa；杆②为木杆，A2＝400cm2，E2＝12GPa，P＝120kN。
解：（1）求各杆的轴力。
取B结点为研究对象[图5-13（b）]，列平衡方程得
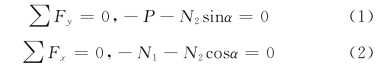
因
，故α＝57.53°，sinα＝0.843，cosα＝0.537，代入式（1）、式（2）解得
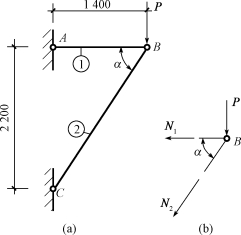
图5-13 例5-6图
N1＝76.4kN（拉杆），N2＝－142.3kN（压杆）
（2）计算杆的变形。
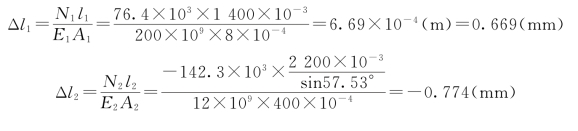
有关建筑力学（第2版）的文章
- 详细阅读
-
电路基本定律：欧姆定律、基尔霍夫定律及其应用详细阅读
根据在电路图上所选电压和电流的参考方向的不同，在欧姆定律表达式可带有正号或负号。对于非线性元器件不遵守欧姆定律。电压、电流的正方向：在应用基尔霍夫定律对电路求解时，首先要在电路图上标定电压、电流和电动势的正方向。当电路比较复杂时，可以使用叠加原理或两次运用戴维南定理。......
2023-06-28
-
元朝脱虎脱及其同党的下场及原因详细阅读
脱虎脱等人之所以捧他“兼尚书省右丞相”，正如他们捧爱育黎拔力八达作“兼尚书令”，无非是借重其声望而已。尚书省右丞相的位置虚悬了六个月，在至大三年五月由脱虎脱调升。再过四天，正月十四，脱虎脱、三宝奴、乐实、保八、王罴，一齐被斩。爱育黎拔力八达之所以一定要杀死脱虎脱等五个人，倒不是因为他们在尚书省发行了至大银钞，而是因为他们太为武宗所亲信。......
2023-10-07
-
模锻工艺及其应用于金属锻件的制造详细阅读
坯料变形时，由于金属的流动受到模膛的限制和引导，从而可以获得与模膛形状一致的锻件。图3-29 三拐曲轴锻造过程图3-30 弯曲类锻件锻造过程但是，由于模锻是整体成形，并且金属流动时，与模膛之间产生很大的摩擦阻力，因此所需设备吨位大，设备费用高。图3-33所示为平锻机工作原理示意图。......
2023-06-28
-
傅里叶定律及其基本概念详细阅读
基本概念①温度场温度场是指某一时刻空间各点温度的总称。傅里叶定律傅里叶在实验研究导热过程的基础上，把热流矢量和温度梯度联系起来，得到q=λgradt 上式就是1822年由傅里叶提出的导热基本定律的数学表达式，亦称为傅里叶定律。傅里叶定律确定了热流密度矢量和温度梯度的关系。......
2023-10-20
-
悬空外延下的GaN纳米柱阵列及其生长现象详细阅读
当2D外延的参数失配很高时，存在一个临界厚度，当厚度小于临界厚度时，生长完成的薄膜开始释放原来吸收的弹性能量，并制造出一些位错。对于GaN/Al2O3，这种现象发生于第1个单层。图2-27 GaN层横截面的SEM图像，使用悬空外延技术，图片摘自文献[DAV 01]。可以在聚结区下观察到一些空隙图2-28 1μm高的GaN纳米柱阵列。MOVPE生长开始于纳米蚀刻掩膜。图2-29 在AlN/SiC纳米柱上的MOVPE再生长。刻蚀掩膜由正方形基元组成，最小的基元边长为40nm[BOU 06]......
2023-06-15
-
砖砌体和钢筋混凝土构造柱组成的组合砖墙：设计详细阅读
构造柱的竖向受力钢筋应在基础梁和楼层圈梁中锚固，并应符合受拉钢筋的锚固要求。组合砖墙砌体结构房屋，应在纵横墙交接处、墙端部和较大洞口的洞边设置构造柱，其间距不宜大于4m。圈梁的截面高度不宜小于240mm；纵向钢筋数量不宜少于4根，直径不宜小于12mm，纵向钢筋应伸入构造柱内，并应符合受拉钢筋的锚固要求；圈梁的箍筋宜采用6mm、间距200mm。组合砖墙的施工程序应为先砌墙后浇混凝土构造柱。......
2023-08-28
-
选择算子及其应用于个体适应度评价！详细阅读
选择操作建立在对个体的适应度进行评价的基础之上。比例选择算子是指个体被选中到下一代群体中的概率与该个体的适应度大小成正比，也叫赌盘选择。......
2023-06-21
相关推荐