如图 6-35所示超静定结构，设各杆件外侧温度升高为t1°C，内侧温度升高t2°C，且 t2＞ t1，去除支座B 的两根链杆，多余约束力为 X1和 X2，基本结构如图 6-35所示。由于基本结构是静定的，在温度改变作用下并不引起内力，所以超静定结构的最终内力只与多余未知力有关。计算结果表明，超静定结构由于温度改变所引起的内力（及反力）与各杆的弯曲刚度EI的绝对值成正比。另外，超静定结构的杆件在温度低的一侧受拉。......
2023-08-30
内力与截面法：探究杆件强度和刚度的密切关系
【摘要】：内力随外力的增大、变形的增大而增大，当内力达到某一限度时，就会引起构件的破坏。内力与杆件的强度、刚度等有着密切的关系。背离截面的轴力称为拉力，指向截面的轴力称为压力。这种假想用一截面将物体截开为两部分，取其中一部分为研究对象，利用平衡条件求解截面内力的方法称为截面法。可见，外力使物体产生内力和变形，不但与外力的大小有关，而且与外力的作用位置及作用方式有关。试求杆内的轴力并作出轴力图。
物体是由质点组成的，物体在没有受到外力作用时，各质点间本来就有相互作用力。物体在外力作用下，内部各质点的相对位置将发生改变，其质点的相互作用力也会发生变化。这种相互作用力由于物体受到外力作用而引起的改变量，称为“附加内力”，简称为内力。
内力随外力的增大、变形的增大而增大，当内力达到某一限度时，就会引起构件的破坏。因此，要进行构件的强度计算就必须先分析构件的内力。内力与杆件的强度、刚度等有着密切的关系。讨论杆件强度、刚度和稳定性问题，必须先求出杆件的内力。
求构件内力的基本方法是截面法。下面通过求解图5-5（a）的拉杆m—m横截面上的内力来阐明这种方法。假想用一横截面将杆沿截面m—m截开，取左段为研究对象，如图5-5（b）所示。由于整个杆件是处于平衡状态的，所以左段也保持平衡，由平衡条件∑X＝0可知，截面m—m上的分布内力的合力必是与杆轴相重合的一个力，且N＝P，其指向背离截面。同样，若取右段为研究对象，如图5-5（c）所示，可得出相同的结果。
图5-5 截面法求内力（拉杆）
对于压杆，也可通过上述方法求得其任一横截面m—m上的轴力N，其指向如图5-6所示。
图5-6 截面法求内力（压杆）
把作用线与杆轴线相重合的内力称为轴力，用符号N表示。背离截面的轴力称为拉力，指向截面的轴力称为压力。通常规定：拉力为正，压力为负。
轴力的单位为牛顿（N）或千牛顿（kN）。
这种假想用一截面将物体截开为两部分，取其中一部分为研究对象，利用平衡条件求解截面内力的方法称为截面法。
综上所述，截面法包括以下三个步骤：
（1）沿所求内力的截面假想地将杆件截成两部分。
（2）取出任一部分为研究对象，并在截开面上用内力代替弃去部分对该部分的作用。
（3）列出研究对象的平衡方程，并求解内力。
【例5-1】杆件受力如图5-7（a）所示，在力P1、P2、P3作用下处于平衡。已知P1＝25kN，P2＝35kN，P3＝10kN，求杆件AB和BC段的轴力。
图5-7 例5-1图
解：杆件承受多个轴向力作用时，外力将杆分为几段，各段杆的内力将不相同，因此要分段求出杆的力。
（1）求AB段的轴力。用1—1截面在AB段内将杆截开，取左段为研究对象[图5-7（b）]，截面上的轴力用N1表示，并假设为拉力，由平衡方程
∑X＝0,N1－P1＝0
N1＝P1＝25(kN)
得正号，说明假设方向与实际方向相同，AB段的轴力为拉力。
（2）求BC段的轴力。用2—2截面在BC段内将杆截开，取左段为研究对象[图5-7（c）]，截面上的轴力用N2表示，由平衡方程
∑X＝0,N2＋P2－P1＝0
N2＝P1－P2＝25－35＝－10(kN)
得负号，说明假设方向与实际方向相反，BC杆的轴力为压力。
若取右段为研究对象[图5-7（d）]，由平衡方程
∑X＝10－N2－P3＝0
N2＝－P3＝－10(kN)
结果与取左段相同。
必须指出：在采用截面法之前，不能随意使用力的可传性和力偶的可移性原理。这是因为将外力移动后就改变了杆件的变形性质，并使内力也随之改变。如将上例中的P2移到A点，则AB段将受压而缩短，其轴力也变为压力。可见，外力使物体产生内力和变形，不但与外力的大小有关，而且与外力的作用位置及作用方式有关。
当杆件受到多于两个轴向外力作用时，在杆的不同截面上轴力将不相同，在这种情况下，对杆件进行强度计算时，必须知道杆的各个横截面上的轴力，最大轴力的数值及其所在截面的位置。为了直观地看出轴力沿横截面位置的变化情况，可按选定的比例尺，用平行于轴线的坐标表示横截面的位置，用垂直于杆轴线的坐标表示各横截面轴力的大小，绘出表示轴力与截面位置关系的图线，该图线就称为轴力图。画图时，习惯上将正值的轴力画在上侧，负值的轴力画在下侧。
【例5-2】杆件受力如图5-8（a）所示。试求杆内的轴力并作出轴力图。
解：（1）为了运算方便，首先求出支座反力。根据平衡条件可知，轴向拉压杆固定端的支座反力只有R，如图5-8（b）所示，取整根杆为研究对象，列平衡方程
∑X＝0,P4＋P2－P1－P3－R＝0
R＝P4＋P2－P1－P3＝－20＋60－40＋25＝25(kN)
（2）求各段杆的轴力。在计算中，为了使计算结果的正负号与轴力规定的符号一致，在假设截面轴力指向时，一律假设为拉力。如果计算结果为正，表明内力的实际指向与假设指向相同，轴力为拉力，如果计算结果为负，表明内力的实际指向与假设指向相反，轴力为压力。
求AB段轴力：用1—1截面将杆件在AB段内截开，取左段为研究对象[图5-8（c）]，以N1表示截面上的轴力，由平衡方程
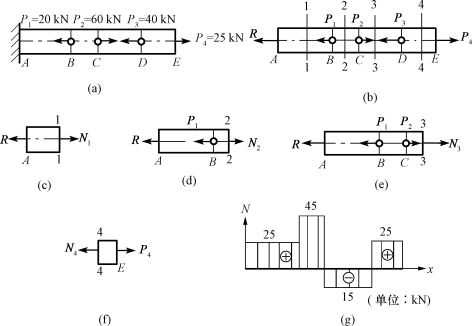
图5-8 杆件受力
∑X＝0,－R＋N1＝0
N1＝R＝25kN（拉力）
求BC段轴力：用2—2截面将杆件截断，取左段为研究对象[图5-8（d）]，由平衡方程
∑X＝0,－R＋N2－P1＝0
N2＝R＋P1＝20＋25＝45（kN）（拉力）
求CD段轴力：用3—3截面将杆件截断，取左段为研究对象[图5-8（e）]，由平衡方程
∑X＝0,－R＋N3－P1＋P2＝0
N2＝R＋P1－P2＝20＋25－60＝－15（kN）（压力）
求DE段轴力：用4—4截面将杆件截断，取右段为研究对象[图5-8（f）]，由平衡方程
∑X＝0,P4－N4＝0
N4＝25（kN）（拉力）
（3）画轴力图。以平行于杆轴的x轴为横轴，垂直于杆轴的N轴为纵轴，按一定比例将各段轴力标在坐标轴上，可作出轴力图，如图5-8（g）所示。
有关建筑力学（第2版）的文章
- 详细阅读
-
例题分析：杆件强度校核计算详细阅读
如图2.1所示的结构上作用荷载F，AB杆为钢杆，其横截面直径d=20mm；BC杆为木杆，其横截面为边长a=100mm的正方形。由于AB杆和BC杆的材料不同，其许用应力也不相同，故需要分别校核其强度。图2.1例题2.1图图2.2计算各杆轴力。取结点B进行分析，建立坐标系，其受力图如图2.2所示。如图2.3所示，AB是刚性杆，在B端受力偶Me作用，已知CD杆的截面积A=500mm2，E=200GPa，[σ]=160MPa，l=1m。图2.3例题2.2图图2.4确定最大荷载Me。CD杆的变形考虑变形后的几何关系，可知......
2023-06-20
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2023-08-26
-
注塑模强度和刚度校核优化方法详细阅读
分流管注塑模动模垫板和斜导柱强度和刚度的校核是为了控制其变形量，以保证熔体在填充过程中不产生溢料飞边及保证产品的壁厚尺寸，并保证注塑件能够顺利脱模。对注塑模强度和刚度的校核应取受力最大，强度和刚度最薄弱的部位进行校核。由于分流管在注塑模中有三种摆放位置，因此就存在着三种注塑模的结构方案。......
2023-06-30
-
型腔和底板的强度及刚度计算方法详解详细阅读
因此在模具设计中要求对强度及刚度加以合理考虑。如果型腔壁厚和底板厚度不够，当型腔中产生的内应力超过型腔材料的许用应力时，型腔便发生强度破坏。强度计算的条件是满足各种受力状态下的材料许用应力。......
2023-06-30
-
如何计算不同形状杆件的内力及应力分析详细阅读
8-1 如图8-15 所示，各杆的AB、BC、CD（或BD）各段横截面上有哪些内力？图8-16题8-2图8-3 如图8-17 所示，斜梁AB 的横截面为正方形，边长为a=100 mm，F=3 kN，试计算其横截面上最大的拉应力和最大的压应力。图8-17题8-3图8-4 开口链环由直径d=12 mm 的圆钢弯制而成，其形状如图8-18 所示。图8-19题8-5图图8-20题8-6图8-7 如图8-21 所示的支架，已知载荷F=45 kN，作用在C 处，支架材料的许用应力[σ]=160 MPa，试选择横梁AC 的工字钢型号。......
2023-06-19
-
大跨度胶合木网格结构的三层杆件节点剪切刚度详细阅读
图5.6设计计算模型中三层杆件正交处节点图5.7三层构件正交节点主向试验加载示意图由于下层主构件由钢柱限位，试验中产生的2 个主构件的位移差为实际节点发生位移的1/2，因此由节点试验推导得到的节点主向剪切刚度应为4.090kN/mm。2 个试件的次向剪切刚度平均值为9.462kN/mm。......
2023-10-07
-
轴向拉（压）杆的强度条件和计算方法优化详细阅读
由式（5-1）可知，拉（压）杆的工作应力，为了保证构件能安全正常地工作，则杆内最大的工作应力不得超过材料的许用应力。即式（5-8）称为拉（压）杆的强度条件。在轴向拉（压）杆中，产生最大正应力的截面称为危险截面。应用强度条件式（5-8）可以解决轴向拉（压）杆强度计算的三类问题。如，表示杆件的强度是满足要求的，否则不满足强度条件。......
2023-06-16
相关推荐