首页理论教育如何计算物体系统的内、外约束反力：理论与实践

如何计算物体系统的内、外约束反力：理论与实践

2025-09-29 理论教育版权反馈

【摘要】：物体系统的平衡是指组成系统的每一物体及系统整体都处于平衡状态。求解物体系统的平衡问题，就是计算出物体系统的内、外约束反力。不论是取整个物体系统或是系统中某一部分作为研究对象，都可根据研究对象所受的力系的类别列出相应的平衡方程去求解未知。注意选择合适的平衡对象，并将其从系统中隔离出来；根据约束性质及作用与反作用定律，分析作用在平衡对象上的力；正确应用平衡方程求解未知力。

物体系统的平衡是指组成系统的每一物体及系统整体都处于平衡状态。

物体系统的平衡的解题方法：

（1）先取整个物体系统作为研究对象，求得某些未知量，再取其中某部分作为研究对象，求出其他未知量。

（2）先取某部分作为研究对象，再取其他或整体作为研究对象逐步求得所有的未知量。

求解物体系统的平衡问题，就是计算出物体系统的内、外约束反力。解决问题的关键在于恰当地选取研究对象，有两种选取的方法。

究竟是先取整体还是先取局部某个物体，一般原则是使所取研究对象的未知力越少越好。不论是取整个物体系统或是系统中某一部分作为研究对象，都可根据研究对象所受的力系的类别列出相应的平衡方程去求解未知。

【例4-6】外伸梁的尺寸及载荷如图4-13所示，试求铰支座A及辊轴支座B的约束力。

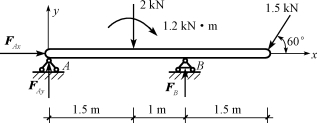
pagenumber_ebook=45,pagenumber_book=36

图4-13　例4-6图

解：取AB梁为研究对象，受力如图4-13所示。建立坐标系，由平面力系的平衡方程

∑X＝0,FAx－1.5cos60°＝0

得

FAx＝0.75kN

∑MA(F)＝0,FB×2.5－1.2－2×1.5－1.5sin60°×(2.5＋1.5)＝0

得

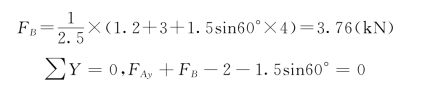
pagenumber_ebook=45,pagenumber_book=36

得

FAy＝2＋1.5sin60°－3.76＝－0.46(kN)

FAy的方向与假设的相反。为校核所得结果是否正确，可应用多余的平衡方程，如

∑MB(F)＝2×1－FAy×2.5－1.2－1.5sin60°×1.5＝0

【例4-7】组合梁受荷载如图4-14所示。已知q＝5kN/m，FP＝30kN，求支座A、B、D的反力。

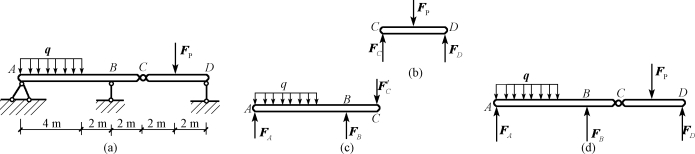pagenumber_ebook=45,pagenumber_book=36 (https://www.chuimin.cn)

图4-14　例4-7图

解：（1）取梁CD段为研究对象，如图4-14（c）所示，由

∑MC＝0,FD×4－FP×2＝0

得

FD＝15kN

（2）取整个组合梁为研究对象，如图4-14（d）所示，由

∑MA＝0,FB×6＋FD×12－q×4×2－FP×10＝0

得

FB＝26.67kN

∑MB＝0,q×4×4－FP×4－FA×6＋FD×6＝0

得

FA＝8.33kN

（3）校核：

∑Fy＝FA＋FB＋FD－q×4－FP＝8.33＋26.67＋15－5×4－30＝0

因此，计算结果准确。

求解有关平面力系平衡问题时，仍应着重于练习受力分析的基本方法。注意选择合适的平衡对象，并将其从系统中隔离出来；根据约束性质及作用与反作用定律，分析作用在平衡对象上的力；正确应用平衡方程求解未知力。

在应用平面力系平衡方程时，应注意以下几个方面的问题：

（1）不要遗漏参加平衡的力。

（2）应用平衡方程时，要特别注意力的投影及力对点的矩的正负号。

（3）应用力矩平衡方程时，可以将力矩中心选为两个未知力作用线的交点。这样，在这一力矩平衡方程中将不包含这两个未知力，而只包含另一个未知力。这就可以通过一个方程求解一个未知力，而无须解联立方程。

（4）根据不同问题的具体情况，可以灵活应用上述三种形式的平衡方程，但所用的方程必须是互相独立的。

（5）要善于利用其他形式的平衡方程验证所得结果的正确性。