力系简化方法及其应用场景

2025-09-29 理论教育版权反馈

【摘要】：设在物体上作用有平面一般力系F1，F2，…，F′n可合成为一个作用于O点的力R′，并称为原力系的主矢[图4-5]，即图4-5力系的简化求主矢R′的大小和方向，可应用解析法。由于主矢等于原力系各力的矢量和，因此主矢R′的大小和方向与简化中心的位置无关。

设在物体上作用有平面一般力系F1，F2，…，Fn，如图4-5（a）所示。为将这一力系简化，首先在该力系的作用面内任选一点O作为简化中心，根据力的平移定理，将各力全部平移到O点[图4-5（b）]，得到一个平面汇交力系F′1，F′2，…，F′n和一个附加的平面力偶系m1，m2，…，mn。

其中平面汇交力系中各力的大小和方向分别与原力系中对应的各力相同，即

各附加的力偶矩分别等于原力系中各力对简化中心O点的矩，即

m1＝MO(F1),m2＝MO(F2),mn＝MO(Fn)

由平面汇交力系合成的理论可知，F′1，F′2，F′3，…，F′n可合成为一个作用于O点的力R′，并称为原力系的主矢[图4-5（c）]，即

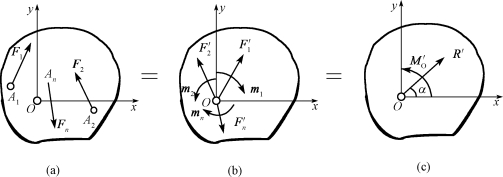
pagenumber_ebook=38,pagenumber_book=29

图4-5　力系的简化

求主矢R′的大小和方向，可应用解析法。过O点取直角坐标系Oxy，如图4-5所示。主矢R′在x轴和y轴上的投影为(https://www.chuimin.cn)

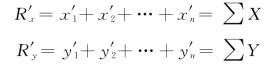
pagenumber_ebook=38,pagenumber_book=29

式中，x′i、y′i和xi、yi分别是力F′i和Fi在坐标轴x轴和y轴上的投影。由于F′i和Fi大小相等、方向相同，所以它们在同一轴上的投影相等。

主矢R′的大小和方向为

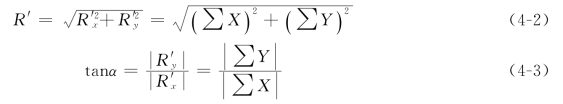
pagenumber_ebook=38,pagenumber_book=29

α为R′与x轴所夹的锐角，R′的指向由∑X和∑Y的正负号确定。

由力偶系合成的理论知，m1，m2，…，mn可合成为一个力偶[图4-5（c）]，并称为原力系对简化中心O的主矩，即

综上所述，得到如下结论：平面一般力系向作用面内任一点简化的结果，是一个力和一个力偶。这个力作用在简化中心，它的矢量称为原力系的主矢，并等于原力系中各力的矢量和；这个力偶的力偶矩称为原力系对简化中心的主矩，并等于原力系各力对简化中心的力矩的代数和。

应当注意，作用于简化中心的力R′一般并不是原力系的合力，力偶矩M′O也不是原力系的合力偶，只有R′与M′O两者相结合才与原力系等效。

由于主矢等于原力系各力的矢量和，因此主矢R′的大小和方向与简化中心的位置无关。而主矩等于原力系各力对简化中心的力矩的代数和，取不同的点作为简化中心，各力的力臂都要发生变化，则各力对简化中心的力矩也会改变，因而，主矩一般随着简化中心的位置不同而改变。