首页理论教育力偶的基本性质及其转动效应

力偶的基本性质及其转动效应

2023-06-16 理论教育版权反馈

【摘要】：力偶不同于力，它具有一些特殊的性质，现分述如下：力偶没有合力，不能用一个力来代替。这说明力偶对其作用面内任一点的矩恒等于力偶矩，而与矩心的位置无关。同一平面内的两个力偶，如果它们的力偶矩大小相等、转向相同，则这两个力偶等效，称为力偶的等效性。图3-10力偶的两个推论由以上分析可知，力偶对物体的转动效应完全取决于力偶矩的大小、力偶的转向及力偶作用面，即力偶的三要素。

力偶不同于力，它具有一些特殊的性质，现分述如下：

（1）力偶没有合力，不能用一个力来代替。由于力偶中的两个力大小相等、方向相反、作用线平行，如果求它们在x轴上的投影，如图3-8所示，设力与x轴的夹角为α，由此可得：

pagenumber_ebook=33,pagenumber_book=24

图3-8　力偶中力在x轴上的投影

∑X＝Fcosα－F′cosα＝0

这说明，力偶在x轴上的投影等于零。

既然力偶在轴上的投影为零，那么力偶对物体只能产生转动效应，而一个力在一般情况下，对物体可产生移动和转动两种效应。

力偶和力对物体的作用效应不同，说明力偶不能用一个力来代替，即力偶不能简化为一个力，因而力偶也不能和一个力平衡，力偶只能与力偶平衡。

（2）力偶对其作用面内任一点的矩都等于力偶矩，与矩心位置无关。

力偶的作用是使物体产生转动效应，所以力偶对物体的转动效应可以用力偶的两个力对其作用面某一点的力矩的代数和来度量。图3-9所示力偶（F，F′），力偶臂为d，逆时针转向，其力偶矩为m＝Fd，在该力偶作用面内任选一点O为矩心，设矩心与F′的垂直距离为h。显然力偶对O点的力矩为

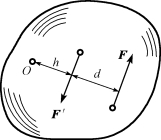
pagenumber_ebook=33,pagenumber_book=24

图3-9　力偶作用面内任一点的矩

MO(F,F′)＝F(d＋h)－F′h＝Fd＝m

此值就等于力偶矩。这说明力偶对其作用面内任一点的矩恒等于力偶矩，而与矩心的位置无关。

（3）同一平面内的两个力偶，如果它们的力偶矩大小相等、转向相同，则这两个力偶等效，称为力偶的等效性（其证明从略）。

从以上性质还可得出两个推论：

（1）在平面内任意移转，而不会改变它对物体的转动效应。例如图3-10（a）所示作用在方向盘上的两个力偶（P1，P′1）与（P2，P′2），只要它们的力偶矩大小相等，转向相同，作用位置虽不同，但转动效应是相同的。

（2）在保持力偶矩大小和转向不变的条件下，可以任意改变力偶的力的大小和力偶臂的长短，而不改变它对物体的转动效应。例如图3-10（b）所示，在攻螺纹时，作用在纹杆上的（F1，F′1）或（F2，F′2）虽然d1和d2不相等，但只要调整力的大小，使力偶矩F1d1＝F2d2，则两力偶的作用效果是相同的。

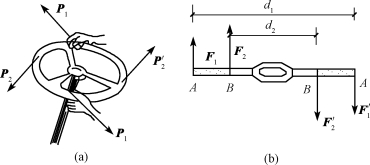
pagenumber_ebook=33,pagenumber_book=24

图3-10　力偶的两个推论

由以上分析可知，力偶对物体的转动效应完全取决于力偶矩的大小、力偶的转向及力偶作用面，即力偶的三要素。因此，在力学计算中，有时也用一带箭头的弧线表示力偶，如图3-11所示，其中箭头表示力偶的转向，m表示力偶矩的大小。

pagenumber_ebook=33,pagenumber_book=24

图3-11　力偶的表示方法