解析力学中的合力矩定理

2023-06-16 理论教育版权反馈

【摘要】：合力矩定理是力学中应用十分广泛的一个重要定理，现用两个汇交力系的情形给以证明。为此，根据合力矩定理，合力R对A点的矩等于F1、F2对A点的矩的代数和。根据合力矩定理可知，分布荷载对某点的矩就等于其合力对该点的矩。

平面汇交力系对物体的作用效应可以用它的合力R来代替。这里的作用效应包括物体绕某点转动的效应，而力使物体绕某点转动的效应由力对该点的矩来度量，因此，平面汇交力系的合力对平面内任一点的矩等于该力系的各分力对该点的矩的代数和。合力矩定理是力学中应用十分广泛的一个重要定理，现用两个汇交力系的情形给以证明。

证明：如图3-4所示，设在物体上的A点作用有两个汇交的力F1和F2，该力系的合力为R。在力系的作用面内任选一点O为矩心，过O点并垂直于OA作y轴。从各力矢的末端向y轴作垂线，用Y1、Y2和Ry分别表示力F1、F2和R在y轴上的投影。由图3-4可见

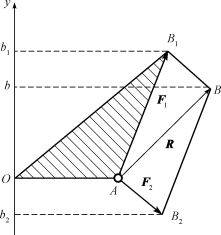
pagenumber_ebook=30,pagenumber_book=21

图3-4　合力矩定理

Y1＝Ob1,Y2＝－Ob2,Ry＝Ob

各力对O点的矩分别为

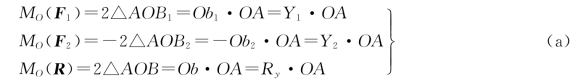
pagenumber_ebook=30,pagenumber_book=21

根据合力矩定理有

Ry＝Y1＋Y2

上式两边同乘以OA得

将式（a）代入式（b）得

MO(R)＝MO(F1)＋MO(F2)

以上证明可以推广到多个汇交力的情况，用公式可表示为

虽然这个定理是从平面汇交力系推证出来的，但可以证明这个定理同样适用于有合力的其他平面力系。

【例3-2】如图3-5所示，每1m长挡土墙所受土压力的合力为R，它的大小R＝200kN，方向如图中所示，求土压力R使墙倾覆的力矩。

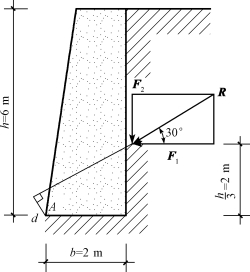
pagenumber_ebook=31,pagenumber_book=22

图3-5　例3-2图

解：土压力R可使挡土墙绕A点倾覆，求R使墙倾覆的力矩，就是求它对A点的力矩。由于R的力臂求解较麻烦，但如果将R分解为两个分力F1和F2，则两分力的力臂是已知的。为此，根据合力矩定理，合力R对A点的矩等于F1、F2对A点的矩的代数和。则

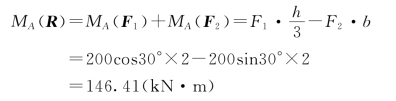
pagenumber_ebook=31,pagenumber_book=22

【例3-3】求图3-6所示各分布荷载对A点的矩。

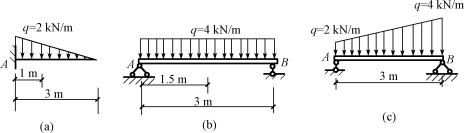
pagenumber_ebook=31,pagenumber_book=22

图3-6　例3-3图

解：沿直线平行分布的线荷载可以合成为一个合力。合力的方向与分布荷载的方向相同，合力作用线通过荷载图的重心，其合力的大小等于荷载图的面积。

根据合力矩定理可知，分布荷载对某点的矩就等于其合力对该点的矩。

（1）计算图3-6（a）所示三角形分布荷载对A点的矩为

（2）计算图3-6（b）所示均布荷载对A点的矩为

MA(q)＝－4×3×1.5＝－18(kN·m)

（3）计算图3-6（c）所示梯形分布荷载对A点的矩。此时为避免求梯形形心，可将梯形分布荷载分解为均布荷载和三角形分布荷载，其合力分别为R1和R2，则有

pagenumber_ebook=31,pagenumber_book=22