力对点的矩是一个代数量，其绝对值等于力的大小与力臂之积，其正负可作如下规定：力使物体绕矩心逆时针转动时取正号；反之取负号。力F对O点的矩，以符号mO表示，即O点称为转动中心，简称矩心。试求两个力对A点的力矩。图3-3二力对A点的力矩分别为计算结果表明，力F2使物体绕A点转动的效果大于力F1所产生的转动效果，板将绕A点顺时针方向转动。......
2023-08-26
力对点的矩及其计算方法
【摘要】：力对点的矩是很早以前人们在使用杠杆、滑车、绞盘等机械搬运或提升重物时所形成的一个概念。若改变力的作用方向，则扳手的转动方向就会发生改变，因此，用F与d的乘积再冠以适当的正负号来表示力F使物体绕O点转动的效应，并称为力F对O点的矩，简称力矩，以符号MO表示，即O点称为转动中心，简称矩心。式中的正负号表示力矩的转向。分别计算图3-3所示的F1、F2对O点的力矩。
力对点的矩是很早以前人们在使用杠杆、滑车、绞盘等机械搬运或提升重物时所形成的一个概念。如图3-1所示，在扳手的A点施加力F，将使扳手和螺母一起绕螺钉中心O转动，这就是说，力有使物体（扳手）产生转动的效应。实践经验表明，扳手的转动效果不仅与力F的大小有关，而且还与点O到力作用线的垂直距离d有关。当d保持不变时，力F越大，转动越快。当力F不变时，d值越大，转动也越快。若改变力的作用方向，则扳手的转动方向就会发生改变，因此，用F与d的乘积再冠以适当的正负号来表示力F使物体绕O点转动的效应，并称为力F对O点的矩，简称力矩，以符号MO（F）表示，即
O点称为转动中心，简称矩心。矩心O到力作用线的垂直距离d称为力臂。
式中的正负号表示力矩的转向。通常规定：力使物体绕矩心作逆时针方向转动时，力矩为正，反之为负。在平面力系中，力矩或为正值，或为负值，因此，力矩可视为代数量。
由图3-2可以看出，力对点的矩还可以用以矩心为顶点，以力矢为底边所构成的三角形的面积的两倍来表示。即
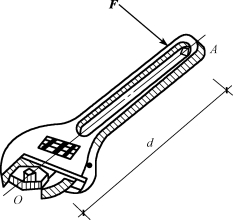
图3-1 扳手施力
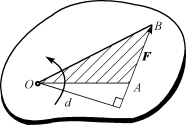
图3-2 力对点的矩
显然，力矩在下列两种情况下等于零：
（1）力等于零；
（2）力的作用线通过矩心，即力臂等于零。
力矩的单位是牛顿·米（N·m）或千牛顿·米（kN·m）。
【例3-1】分别计算图3-3所示的F1、F2对O点的力矩。
图3-3 例3-1图
解：由式（3-1），有
MO(F1)＝F1·d1＝10×1×sin30°＝5(kN·m)
MO(F2)＝－F2·d2＝－30×1.5＝－45(kN·m)
有关建筑力学（第2版）的文章
- 详细阅读
-
压边力和拉深力的计算方法详细阅读
压边力的大小应允许在一定范围内调节。一般来说，随着拉深系数的减小，压边力许可调节范围减小，这对拉深工作是不利的，因为当压边力过大时，就会产生破裂，压边力过小时，会产生起皱，即拉深的工艺稳定性不好。相反，拉深系数较大时，压边力可调节范围增大，拉深工艺稳定性较好。表4-48 采用或不采用压边装置的条件为了更准确地估算是否需要压边装置，还应考虑拉深系数的大小。......
2023-06-26
-
常数和位点的结合计算方法详细阅读
图2.2.52-en与不同浓度dsDNA相互作用的常规脉冲伏安图及摩尔结合分数Xb与[DNA]的非线性拟合曲线常规脉冲伏安法经常应用于测定电活性小分子和生物大分子之间的结合常数，因为常规脉冲伏安法的极限电流能准确地反应具有电活性分子的游离态和dsDNA结合态配合物之间的形态转换[26，45]。......
2023-06-22
-
新媒体技术对创造力的破坏及其影响详细阅读
每一次技术革命对人类身心与生存而言都是一把双刃剑，前两次工业革命带来的人机分离，虽然有效地提高了生产效率，但却给人类身心造成巨大伤害。熊彼特的“创造性破坏”概念最初是一个经济学概念，后被广泛应用于人文社会科学不同分支与领域，近年来传播学者将其引入新媒体研究，探讨数字化技术应用给社区报、政府管理变革等产生的“破坏性”与“创造性”影响。......
2023-11-25
-
地震力计算方法及示例详细阅读
《抗震规范》规定，桥梁抗震设计时，地震力的计算，一般情况下桥墩应采用反应谱理论，桥台采用静力法。对于满足《抗震规范》第6.1.3条要求的规则桥梁可按单振型反应谱方法进行E1和E2地震作用下结构的内力和变形计算。......
2023-08-28
-
传统协调技术及其特点的优化详细阅读
如果用空间立体的协调依据，则其协调过程的特点是可连续地确定空间形状。图3-9为传统的飞机制造协调原理图。模线样板—标准样件协调方法是一种适用于成批生产小型飞机的协调技术。图3-9传统的飞机制造协调原理图①工艺装备的制造必须严格按照协调路线规定的先后次序进行，平行作业受到很大的限制。......
2023-07-18
-
专利权及其特点的分析介绍详细阅读
专利权，是指由专利在一定期限内依法产生的专有权利；或者说，是公民、法人或者其他组织对其发明创造在一定期限内依法享有的垄断权。在某些特殊情况下，专利权可简称为“专利”。但是，同样的发明创造在不同的法域可以分别被批准为专利。另一方面，除法律另有规定外，任何人未经专利权人许可，不得为生产经营目的实施其专利。......
2023-07-03
-
磁路及其计算方法详细阅读
图3-3 磁路中的磁通用以激励磁路中磁通的载流线圈称为励磁线圈，励磁线圈中的电流称为励磁电流。若励磁电流为交流，磁路中的磁通是随时间变化的，这种磁路称为交流磁路。例如图3-5所示磁路由两段截面不同的铁磁材料和一段空气隙组成。值得指出的是，由于铁心饱和时磁路为非线性，因此铁心磁路计算时不能应用线性叠加原理。......
2023-06-30
相关推荐