、Fn 组成的平面汇交力系。因此，平面汇交力系平衡的充分与必要的几何条件是：力的多边形自行封闭。图3-8平面汇交力系平衡的几何条件平面汇交力系；平面汇交力系合成；力多边形自行封闭用几何法解题所获得解答的精确程度受作图质量的影响。......
2023-06-19
用几何法合成力系
【摘要】：矢量关系式为或简写为若力系中各力的作用线位于同一条直线上，在这种特殊情况下，力多边形变成一条直线，合力为需要指出的是，利用几何法对力系进行合成，对于平面汇交力系，并不要求力系中各分力的作用点位于同一点，因为根据力的可传性原理，只要它们的作用线汇交于同一点即可。另外，几何法只适用于平面汇交力系，而对于空间汇交力系来说，由于作图不方便，用几何法求解是不适宜的。
首先回顾用几何法合成两个汇交力。如图2-1（a）所示，设在物体上作用有汇交于O点的两个力F1和F2，根据力的平行四边形法则，可知合力R的大小和方向是以两力F1和F2为邻边的平行四边形的对角线来表示，合力R的作用点就是这两个力的汇交点O。也可以取平行四边形的一半，即利用力的三角形法则求合力，如图2-1（b）所示。
对于由多个力组成的平面汇交力系，可以连续应用力的三角形法则进行力的合成。设作用于物体上O点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2（a）所示。应用力的三角形法则，首先将F1与F2合成得R1，然后把R1与F3合成得R2，最后将R2与F4合成得R，力R就是原汇交力系F1、F2、F3、F4的合力，图2-2（b）所示即是此汇交力系合成的几何示意，矢量关系的数学表达式为
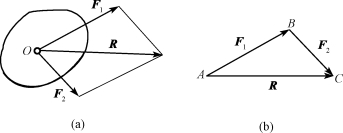
图2-1 几何法合成两个汇交力
实际作图时，可以不画出图中虚线所示的中间合力R1和R2，只要按照一定的比例将表达各力矢的有向线段首尾相接，形成一个不封闭的多边形，如图2-2（c）所示。然后再画一条从起点指向终点的矢量R，即为原汇交力系的合力，如图2-2（d）所示。把由各分力和合力构成的多边形abcde称为力多边形，合力矢是力多边形的封闭边。按照与各分力同样的比例，封闭边的长度表示合力的大小，合力的方位与封闭边的方位一致，指向则由力多边形的起点至终点，合力的作用线通过汇交点。这种求合力矢的几何作图法称为力多边形法则。
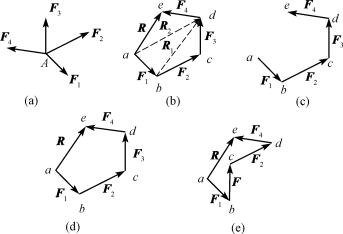
图2-2 平面汇交力系合成（几何法）
从图2-2（e）还可以看出，改变各分力矢相连的先后顺序，只会影响力多边形的形状，但不会影响合成的最后结果。
将这一做法推广到由n个力组成的平面汇交力系，可得结论：平面汇交力系合成的最终结果是一个合力，合力的大小和方向等于力系中各分力的矢量和，可由力多边形的封闭边确定，合力的作用线通过力系的汇交点，合力的起点为第一个力的箭尾，合力终点为最后一个力的箭头，构成一个封闭几何多边形。矢量关系式为
或简写为
若力系中各力的作用线位于同一条直线上，在这种特殊情况下，力多边形变成一条直线，合力为
需要指出的是，利用几何法对力系进行合成，对于平面汇交力系，并不要求力系中各分力的作用点位于同一点，因为根据力的可传性原理，只要它们的作用线汇交于同一点即可。另外，几何法只适用于平面汇交力系，而对于空间汇交力系来说，由于作图不方便，用几何法求解是不适宜的。
对于由多个力组成的平面汇交力系，用几何法进行简化的优点是直观、方便、快捷，画出力多边形后，按与画分力同样的比例，用尺子和量角器即可量得合力的大小和方向。但是，这种方法要求作图精确，否则误差会较大。
有关建筑力学（第2版）的文章
- 详细阅读
-
平面力系合成的解析法及平衡条件详细阅读
若已知Fx、Fy 值，可求出F 的大小和方向，即2.平面汇交力系合成的解析法设刚体上作用有一个平面汇交力系F1、F2、…应用式（3-6）、式（3-7）计算合力大小和方向的方法，称为平面汇交力系合成的解析法。案例3-4 求图3-12 所示平面汇交力系的合力。式（3-9）称为平面汇交力系的平衡方程，这是相互独立的两个方程，所以只能求解两个未知量。由于滑轮的大小可忽略不计，故这些力可看作是平面汇交力系。......
2023-06-19
-
建筑力学第3版：平面汇交力合成几何法详细阅读
在第一章中，已对几何法进行了介绍，知道了两个汇交于一点的力F1和F2如何应用力的平行四边形法则和三角形法则求它们的合力R。设作用于物体上A点的力F1、F2、F3、F4组成平面汇交力系，现求其合力，如图2-2所示。这种由各分力和合力构成的多边形abcde称为力多边形。这种求合力矢的几何作图法被称为力多边形法。拉力F1、F2、F3的作用力汇交于O点，构成平面汇交力系。......
2023-08-26
-
用添加几何关系求解几何问题详细阅读
单击画直线命令，画直线的端点分别在AB、AC和BC上，同时利用智能尺寸标注AD=15mm，单击添加几何关系，按住Ctrl键选中AC和EF，从属性管理器中选中平行关系，如图1-38所示。单击画圆命令，以DF为直径画圆，然后再以F点为圆心，FE长为半径画圆，利用添加几何关系使刚才画的这两个圆相等，具体操作同上一步类似，如图1-39所示。......
2023-11-21
-
解析法：另一种常用的求解平面汇交力系合成的方详细阅读
求解平面汇交力系合成的另一种常用方法是解析法。图2-3力的分解图2-4各力在坐标轴上的投影解：根据式（2-3）、式（2-4），列表计算如下：2.合力投影定理为了用解析法求平面汇交力系的合力，必须先讨论合力及其分力在同一坐标轴上投影的关系。图2-8例2-2图解析法。......
2023-06-16
-
平面力系合成与平衡的方法分析详细阅读
平面汇交力系合成的几何法设一刚体受到平面汇交力系F1、F2、F3、F4 的作用，各力的作用线汇交于一点A。若平面汇交力系有n 个力，用FR 表示合力矢，则有合力矢对刚体的作用与原力系对该刚体的作用是等效的。图3-17几何法求约束力根据平面汇交力系平衡的几何条件，此3 个力可以组成一个封闭的三角形。......
2023-06-26
- 详细阅读
-
用数学统计法分析数据详细阅读
数理统计法有合成总库容法、直接总库容法和随机模拟法等。某多年调节水库，已知多年平均年径流量＝6000万m3、Cv＝0.6、Cs＝2Cv，年供水量W用＝4500万m3，p设＝85%。已知Cv＝0.3、Cs＝3Cv，α＝0.8，p设＝90%，求β多。因为Cs≠2Cv，故需先用式变换参数。当代表年的来水、用水确定后，就可采用年调节兴利调节计算方法确定年库容。在不计损失的基础上，可进一步计入损失。......
2023-06-21
相关推荐