机车齿轮的材料大致可分为调质钢、渗氮钢及渗碳钢三大类。大连机车车辆有限公司采用17CrNiMo6钢制造的HXD5型大功率机车牵引齿轮,并经渗碳淬火。一般机床齿轮常用钢材及其热处理工艺见表1-22。表1-22 一般机床齿轮常用钢材及其热处理工艺7.航空齿轮用钢及其热处理航空齿轮是用来传递动力和改变运行速度的,因此在功率传递机构如减速器中,需要使用各种形式的齿轮。部分齿轮钢采用优质渗氮钢进行渗氮热处理。......
2023-06-29
(一)弹簧的功用
弹簧是一般机械中的常用零件之一,它是靠弹性变形而工作的弹性元件。在外载作用下,弹簧产生较大的弹性变形,把机械功或动能转变为变形能,在卸载时,弹簧恢复变形,把变形能变为动能或机械功。由于弹簧具有这样的特性,它常应用在以下几方面:
(1) 缓冲和吸振。如车辆弹簧,各种缓冲器中的弹簧等。
(2) 控制运动。如离合器、制动器和凸轮机构中的控制弹簧等。
(3) 储存能量。如钟表或仪表中的发条弹簧、枪机弹簧等。
(4) 测量力或力矩。如测力器弹簧秤中的弹簧等。
(二)弹簧的类型
为了满足不同的工作要求,弹簧有各种不同的类型。按照承受载荷的不同,弹簧可分为拉伸弹簧、压缩弹簧、扭转弹簧和弯曲弹簧等四种。按照弹簧外形的不同,又可分为螺旋弹簧、环形弹簧、碟形弹簧、盘簧和板簧等。除金属弹簧外,还有空气弹簧和橡胶弹簧等。表3-10 列出了弹簧的基本类型。
表3-10 弹簧的基本类型
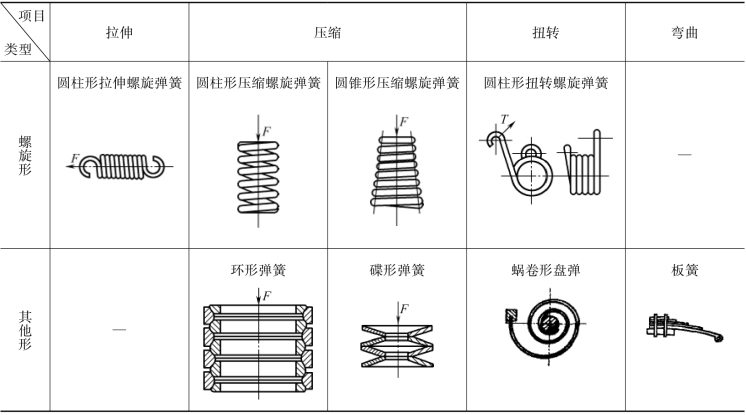
在一般机械中,最常用的是圆柱螺旋弹簧,它由圆剖面弹簧丝卷绕制成。本节主要介绍这类弹簧的结构形式、设计理论和计算方法。
(三)弹簧的材料
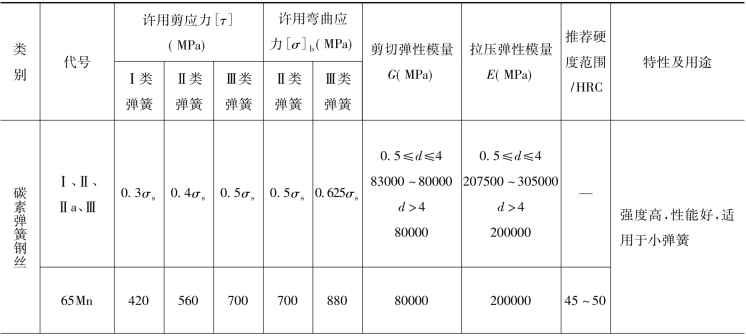
弹簧通常承受变载荷和冲击载荷,需要有较大的弹性变形,所以对弹簧的材料要求较高。弹簧材料除应具有较高的强度极限、屈服极限外,还应具有较高的弹性极限和疲劳极限,一定的冲击韧性和良好的热处理性能。工程上常用的弹簧材料有碳素弹簧钢、合金弹簧钢、不锈弹簧钢、铜合金以及橡胶和塑料等。常用弹簧材料及性能见表3-11。
表3-11 常用弹簧材料及性能
续表
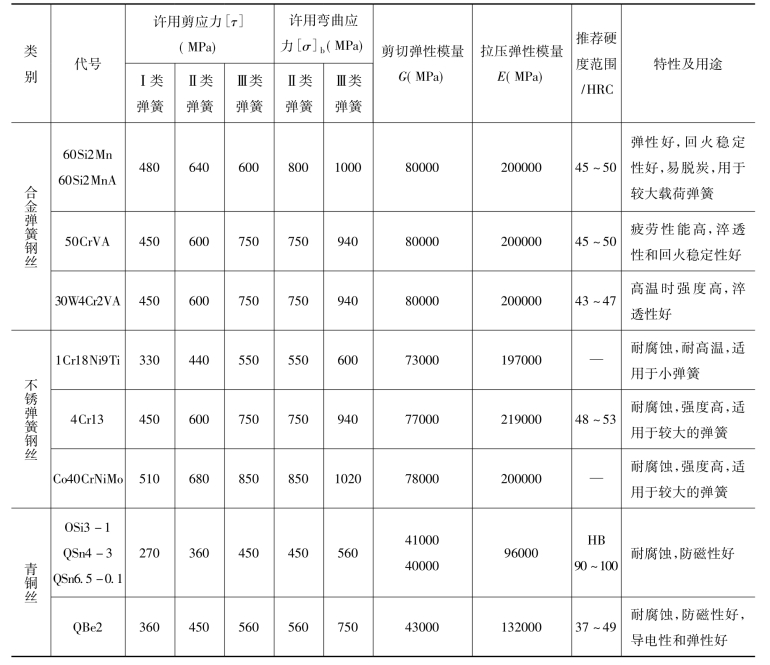
选择材料时,应充分考虑弹簧的工作条件( 载荷大小及性质、工作延续时间、工作温度和周围介质的情况)、功用、重要性和经济性等因素。在一般情况下应优先采用碳素弹簧钢,其含碳量在0.6% ~0.9%(65#和70#钢) ,按其机械性能分为Ⅰ组、Ⅱ组、Ⅱa 组及Ⅲ组。通常Ⅰ组用于重要场合,Ⅲ组用于不重要场合,一般机械中的弹簧大多采用Ⅱ组。当弹簧在工作时要承受较大的变载荷或冲击载荷,应采用合金弹簧钢(60Si2MnA、50CrVA) 。当弹簧在潮湿或酸碱等化学腐蚀介质中工作时,应采用不锈弹簧钢(1Cr18N19Ti、4Cr13) 或铜合金( QSi3-1、QSn4-3) 。
(四)弹簧的许用应力
弹簧的许用应力与材料及载荷性质有关。弹簧载荷性质可分为以下三类:
Ⅰ类:受变载荷循环次数为N >106的弹簧。
Ⅱ类:受变载荷循环次数为N=103~106的弹簧,以及受冲击载荷的弹簧。
Ⅲ类:受变载荷循环次数为N <103的弹簧,以及受静载荷的弹簧。
根据弹簧材料及以上分类,由表3-10 可查得弹簧的许用应力。
(五)弹簧的制造
螺旋弹簧的制造过程包括:卷绕、两端加工、热处理和工艺试验等。为了提高承载能力,还可在弹簧制成后进行强压处理或喷丸处理。
卷绕分冷卷和热卷两种。当钢丝直径较小( d <8mm) 或弹簧直径较大易于卷绕时,一般采用冷卷法。冷卷弹簧常用经过热处理的冷拉材料,在常温下卷绕成型,不再淬火,只需进行低温回火以消除内应力。当簧丝直径较大( d >8mm) ,或簧丝直径虽小于8mm 但弹簧直径较小,则采用热卷法。热卷弹簧是在热状况下卷绕成型,卷好后必须进行淬火及中温回火处理。
压缩弹簧两端一般应并紧且磨平。拉伸、扭转弹簧的两端要制作挂钩或工作臂,以便固定和加载。
工艺试验是使螺旋弹簧承受2 ~3 次极限载荷后,检查热处理是否合格,有无缺陷,是否符合规定公差等。
强压处理是将弹簧在超过极限载荷下,受载6 ~48h。喷丸处理是用一定的速度喷射钢丸或铁丸撞击弹簧。这两种强化措施,都能使簧丝表层产生塑性变形,因而存在残余应力。
由于残余应力的方向和工作应力的方向相反,从而提高弹簧的承载能力。
(六)圆柱螺旋弹簧的基本特性
1.基本几何参数 图3-30 所示为圆柱螺旋压缩和拉伸弹簧基本几何参数,包括:d( 弹簧丝直径)、D( 弹簧外径)、D2( 弹簧中径)、D1( 弹簧内径)、α( 螺旋升角)、t( 节距)、H0( 自由高度)、n1( 弹簧总圈数)、L( 弹簧展开长度) 。各几何参数关系为:
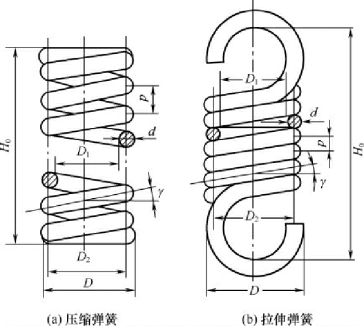
图3-30 圆柱螺旋压缩和拉伸弹簧的基本参数
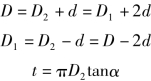
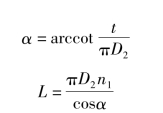
或
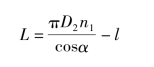
式中:l 为拉伸弹簧挂钩的展开长度。以上各式对圆柱扭转螺旋弹簧完全适用,此时l 为扭转弹簧的工作臂的展开长度。压缩弹簧的螺旋升角α 一般为5° ~9°,拉伸和扭转弹簧的螺旋升角α 很小。螺旋线方向一般采用右旋。
2.弹簧指数 弹簧中径D2与弹簧丝直径d 之比称为弹簧指数,以C 表示,即 弹簧指数又称旋绕比,它是反应弹簧特性的一个重要参数。当弹簧直径d 一定时,C 值越小,弹簧中径D2越小,弹簧越硬( 刚度越大) ;反之,弹簧越软( 刚度越小) 。C 值过小,卷绕弹簧困难,使簧圈内侧产生的应力过大,导致弹簧损坏。C 值过大,弹簧的径向尺寸过大,易使弹簧颤动,不稳定。
弹簧指数又称旋绕比,它是反应弹簧特性的一个重要参数。当弹簧直径d 一定时,C 值越小,弹簧中径D2越小,弹簧越硬( 刚度越大) ;反之,弹簧越软( 刚度越小) 。C 值过小,卷绕弹簧困难,使簧圈内侧产生的应力过大,导致弹簧损坏。C 值过大,弹簧的径向尺寸过大,易使弹簧颤动,不稳定。
在设计弹簧时,通常需预选C 值,工程上一般取C =4 ~14,常取C =5 ~8。C 值的选取范围,可参见表3-12。
表3-12 弹簧指数C 的选取范围

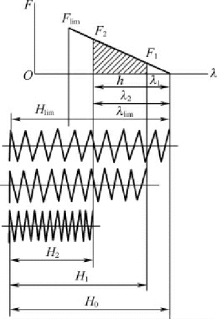
图3-31 压缩弹簧的特性线
3.弹簧特性线 为了清晰地表明工作过程中弹簧的载荷与变形( 或高度) 之间的关系,常绘出载荷与变形的关系曲线,称为弹簧特性线。对于等节距的圆柱螺旋弹簧,其受载与变形成正比关系,因而其特性线为一直线。这个关系对拉簧、压簧和扭簧均适用。
(1) 压缩弹簧特性线:如图3-31 所示,图中H0为弹簧的自由高度,即弹簧未受载荷时的高度。安装弹簧时,通常使弹簧预先承受一定载荷F1,使其可靠地稳定在安装位置上,F1称为弹簧的最小工作载荷( 预加载荷) ,在F1的作用下,弹簧的高度被压缩到H1,其压缩变形量为λ1。F2为弹簧工作时受到的最大工作载荷,在F2的作用下,弹簧高度被压缩到H2,其压缩变形量增加到λ2。λ2-λ1=h,即弹簧的工作行程。Flim为弹簧的极限载荷,亦即在Flim作用下弹簧丝内的应力达到了弹簧材料的弹性极限,此时相应的弹簧高度为Hlim,压缩变形量为λlin。最大工作载荷F2通常由机构工作条件决定,由于在工作过程中一般不希望弹簧失去直线的特性关系,常取F2≤0.8Flim。而最小工作载荷F1=(0.1 ~0.5) F2。
压缩弹簧在载荷作用下完全并紧( 各圈接触) 的理论高度称为并紧高度Hb,此时所作用的载荷为并紧载荷Fb,对应的压缩变形量为λb。显然,一般λlim应略小于或等于λb,即λlim≤λb。
(2) 拉伸弹簧特性线:如图3-32 所示。按照卷绕方法不同,拉伸弹簧分为无初拉应力和有初拉应力两种。
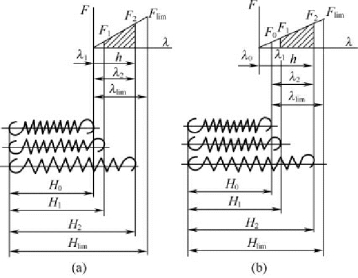
图3-32 拉伸弹簧的特性线
图3-32( a) 为无初应力的特性线,它和压缩弹簧的特性线相同,但其中F 为拉伸载荷,λ为伸长变形量。图3-32( b) 为有初应力的特性线。这种拉簧在卷绕后各圈相互并紧并使弹簧在自由状态下便有初拉力F0的作用,其相应的拉伸变形量为λ0。
当承受载荷时,首先要克服假想变形量λ0,弹簧才开始伸长。它适用于弹簧的轴向空间较小的地方。在一般情况下,F0约具有如下数值:弹簧丝直径d≤5mm,F0≈1/3Flim;d≥5mm,F0≈1/4Flim。
扭转弹簧特性线如图3-33 所示。由于扭转弹簧所受的载荷为扭矩,产生的变形为扭转角,所以特性线表示出扭矩T 与扭转角φ 之间的关系。
图3-33( a) 是用极坐标表示的特性线,图3-33( b) 是用直角坐标表示的特性线。T1、T2和Tlim,分别为扭转弹簧的最小工作扭矩( 预加扭矩) ,最大工作扭矩和极限扭矩; φ1、φ2和φlim是相应于T1、T2和Tlim时的扭转角;φ2-φ1=φ,即弹簧的工作行程。同样,最大工作扭矩T2通常由机构工作条件而定,常取T2<0.8Tlim,T1=(0.1 ~0.5) T2。
在弹簧的工作图上应画出弹簧的特性线,作为试验和检验的依据。此外,设计计算弹簧时,利用特性线来分析弹簧受载和变形的关系也甚为方便。
应该指出,由于弹簧类型,结构的不同,弹簧特性线,除上述的直线型外,还有曲线或折线( 如渐增型、渐减型和混合型等) ,见图3-34( a)、( b) 和( c) 。在纺织机械中的弹簧以直线型特性线最常见。
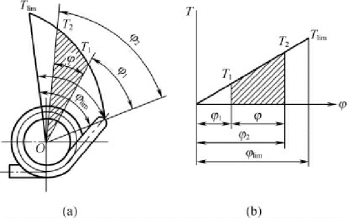
图3-33 扭转弹簧的特性线
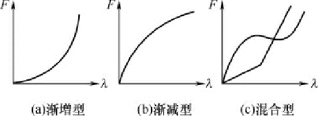
图3-34 弹簧特性线的型式
4.弹簧刚度 产生单位变形所需的载荷称为弹簧刚度,以k 表示。对图3-30 ~图3-33所示直线型特性线的弹簧,弹簧刚度为常数,其载荷和变形有如下关系:
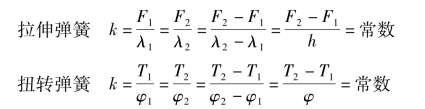
显然,特性线的斜率越大,弹簧刚度k 也越大,弹簧越硬;反之,弹簧越软。工程上把直线型特性线的弹簧称为定刚度弹簧,而把曲线或折线型特性线的弹簧称为变刚度弹簧。后者更适合承受有动载荷或冲击载荷的场合。
有关纺织机械基础的文章

机车齿轮的材料大致可分为调质钢、渗氮钢及渗碳钢三大类。大连机车车辆有限公司采用17CrNiMo6钢制造的HXD5型大功率机车牵引齿轮,并经渗碳淬火。一般机床齿轮常用钢材及其热处理工艺见表1-22。表1-22 一般机床齿轮常用钢材及其热处理工艺7.航空齿轮用钢及其热处理航空齿轮是用来传递动力和改变运行速度的,因此在功率传递机构如减速器中,需要使用各种形式的齿轮。部分齿轮钢采用优质渗氮钢进行渗氮热处理。......
2023-06-29

子任务一原辅料及预处理一、酱油生产主要原料原料质量决定着酱油产品的质量,原料选取标准:一是蛋白质含量较高,碳水化合物适量,有利于制曲和发酵;二是无毒无异味,优质豆类和淀粉类物质;三是资源丰富,价格低廉,容易收集,便于运输和保管,有利于原料的综合利用。(一)蛋白质原料蛋白质是构成酱油中氮元素及鲜味的主要来源,也是构成酱油色素的基础物质。......
2023-12-07

按汽车碰撞后导致的损伤现象不同,汽车碰撞损伤可归纳为五大类,即侧弯、凹陷、折皱或压溃、菱形损坏、扭曲等,如图7-14所示。承载式车身汽车车身也能够发生侧面损坏。当一辆汽车以高速撞击到路边或高级公路中间分界之安全岛时,有可能发生扭曲型损坏。后侧车角发生碰撞也常发生扭曲损坏,仔细检查能发现板件不明显的损坏,然而真正的损坏一般隐藏在下部。......
2023-08-10

灰铸铁齿轮多用于开式齿轮传动。表1-29 常用灰铸铁、球墨铸铁的力学性能1.齿轮用灰铸铁及其热处理灰铸铁的选用 灰铸铁的抗弯及抗冲击能力很差,但它易于铸造、易切削,具有良好的耐磨性和减振性、最小的缺口敏感性、成本低。......
2023-06-29

为了对比,采用了两组弹簧进行实验,其原长均为36mm,而刚度系数分别为根据上述仿真结果、优化设计出的2.4N/mm,和不满足设计要求的3N/mm。......
2023-06-15

因为只有当食物十分新鲜时及时地冷冻,才能保证食物鲜美的味道。保鲜膜外须加上保鲜袋为了防止保鲜膜本身的细孔导致保存食物时出现干燥或串味等现象,要在速冻食物时放入封好的保鲜袋中,但加了保鲜膜和保鲜袋的食物不能直接使用微波炉解冻。所以,针对此类食材应隔绝空气进行保存。解冻方法若时间充足则将肉片放入冰箱保鲜室自然解冻,反之则可使用微波炉解冻。......
2023-07-29

Pro/ENGINEER软件的野火版提供了挠性元件的装配功能。最常见的挠性元件为弹簧,由于弹簧零件在装配前后的形状和尺寸均会产生变化,所以装配弹簧需要较特殊的装配方法和技巧。下面以图6.2.1中的弹簧装配为例,说明挠性元件装配的一般操作过程。图6.2.1 挠性元件的装配Stage1.设置目录将工作目录设置至D:\proewf5.2\work\ch06.02,打开文件spring.prt。图6.2.3 定义装配约束图6.2.4 将弹簧变成挠性元件Stage5.验证弹簧的挠性Step1.在模型树中右击零件,选择命令。......
2023-06-20
相关推荐