任务要求绘制缝纫机踏板机构的运动简图，分析其组成及运动特点。图2.6双曲柄机构图2.7惯性筛双曲柄机构中，当两曲柄长度相等，连杆与机架的长度也相等时，称为平行双曲柄机构或平行四边形机构。图2.9公共汽车车门启闭机构双摇杆机构铰链四杆机构的两个连架杆均为摇杆时，称为双摇杆机构，如图2.10所示。......
2023-06-30
设计四杆平面连杆机构，计算急回运动的速比系数
【摘要】：最常见的平面连杆机构是四杆机构。不论是曲柄摇杆机构或者其他类型的平面连杆机构，只要机构的极位夹角θ 不为零，则该机构就有急回运动，其行程速比系数K 仍可用式(2-3) 计算。 按给定的连杆位置设计四杆机构。
最常见的平面连杆机构是四杆机构。在如图2-11 所示的连杆机构中，其固定不动的构件4 称为机架;与机架相连的构件称为连架杆;其中能做整周转动的连架杆1 称为曲柄;杆2 称为连杆，不能做整周转动的连架杆3 称为摇杆，构件4 则称为机架。
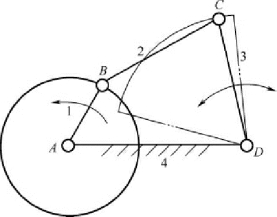
图2-11 平面四杆机构
四杆机构的常用形式有以下五种:
(一)曲柄摇杆机构
在曲柄摇杆机构中，两连架杆中一个为曲柄，另一个为摇杆。如图2-11 所示曲柄和摇杆可分别作为主动件和从动件。当曲柄为主动件，摇杆为从动件时，可将曲柄的连续转动变成摇杆的往复摆动。
(二)双摇杆机构
在双摇杆机构中，两连架杆均为摇杆，如图2-12 所示。
(三)曲柄滑块机构
曲柄滑块机构如图2-13、图2-14 所示，从原理上说，曲柄滑块机构是曲柄摇杆机构的一种演化，当曲柄摇杆机构中的摇杆的长度趋于无穷时，曲柄摇杆机构就变成了曲柄滑块机构。曲柄滑块机构可以把曲柄的旋转运动变换成滑块的往复直线运动。
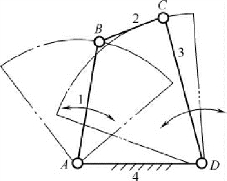
图2-12 双摇杆机构
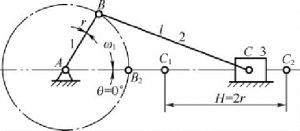
图2-13 对心曲柄滑块机构
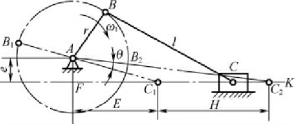
图2-14 偏置曲柄滑块机构
(四)偏心轮机构
偏心轮机构也是曲柄摇块机构和曲柄滑块机构的一种演化。当曲柄很短时，在曲柄上要做出两个转动副非常困难，往往采用转动中心与几何中心不重合的偏心轮来代替曲柄。两中心之间的距离e 称为偏距，其值即为曲柄长度。这种将偏心轮代替曲柄的四杆机构一般称为偏心轮机构( 图2-15) 。
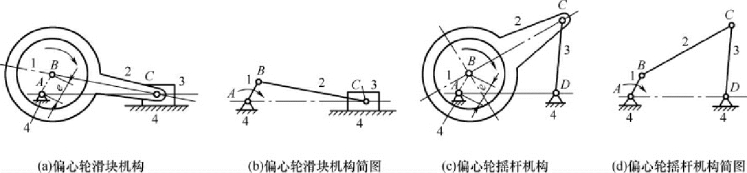
图2-15 偏心轮机构
(五)四杆机构的基本特性
1.急回特性 如图2-16 所示，当曲柄匀速转动时，由于摇杆处于两极限位置时，曲柄的转角不同，因此摇杆向左和向右的速度就不相等，形成速度差。这个特性一般叫做急回特性。当从动摇杆处于左、右极限位置时，主动曲柄两位置所夹的锐角θ 称为极位夹角，从动摇杆两极限位置间的夹角φ称为摇杆的摆角。
为了表明急回特性的相对程度，通常用v2与v1的比值K来衡量，K 称为行程速比系数，即:
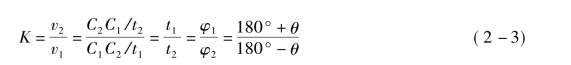
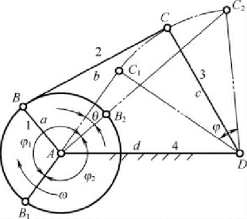
图2-16 急回特性
当给定行程速比系数K 后，机构的极位夹角可由下式算出:
由上式分析可知，平面连杆机构有无急回运动取决于有无极位夹角θ。不论是曲柄摇杆机构或者其他类型的平面连杆机构，只要机构的极位夹角θ 不为零，则该机构就有急回运动，其行程速比系数K 仍可用式(2-3) 计算。
2.压力角 如图2-17 所示，连杆推动摇杆摆动时，连杆作用于摇杆的力方向，与摇杆连接点的运动方向之间的夹角α 称为压力角。其值的大小与力的作用效果有关，其值越小，效果就越好。
作用力F 与分力Fn间所夹的锐角γ 称为传动角。由图2-17 可以看出，α +γ =90°，故α与γ 互为余角。由于传动角γ 可以从机构运动简图上直接观察来表示，故通常用γ 值来衡量机构的传力性能。γ 值越大，则α 值越小，机构的传力性能就越好。
在机构运动过程中，传动角γ 的大小是随机构位置的改变而改变的。为了确保机构能正常工作，应使一个运动循环中最小传动角γmin为40° ～50°，具体数值可根据传递的功率而定。
图2-17 压力角
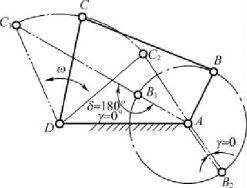
图2-18 死点位置
3.死点位置 如图2-18 所示，曲柄摇杆机构中，当摇杆作为主动件，并且摇杆在两个极限位置时，由于摇杆作用于连杆的力的方向通过了曲柄的转动中心，这时摇杆就无法推动曲柄转动，这个位置叫做死点位置。
就传动机构而言，机构存在死点是不利的，应该采取措施使机构能顺利通过死点位置。对于连续运转的机械，可以利用从动件的惯性来通过死点位置。
机构的死点位置并非总是起消极作用。在工程实际中，不少场合也利用机构的死点位置来实现一定的工作要求。
4.平面四杆机构的设计 平面四杆机构的设计的主要任务是根据给定的运动条件，用图解法、解析法或实验法来确定机构运动简图的尺寸参数。有时，为了使设计更为合理，还需考虑几何条件和动力条件( 最小传动角γmin) 等。
(1) 按给定的行程速比系数设计四杆机构: 在设计该类的四杆机构时，通常按实际需要先给定行程速比系数K 值，然后根据机构在极限位置时的几何关系，结合有关的辅助条件来确定机构运动简图的尺寸参数。
①曲柄摇杆机构:已知摇杆的长度lCD，摇杆的摆角φ 和行程速比系数K 值，然后根据机构在极限位置时的几何关系，结合有关辅助条件来确定机构运动简图的尺寸参数。
设计的实质是确定固定铰链中心A 的位置，定出其他三个构件的尺寸lAB、lBC和lAD。其设计步骤如下:
a.由给定的行程速比系数K，计算出极位夹角θ。
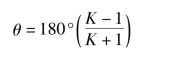
b.任选一固定铰链点D，选取长度比例尺μl并按摇杆长lCD和摆角φ 作出摇杆的两个极限位置C1D 和C2D，如图2-19 所示。
图2-19 按K 值设计曲柄摇杆机构
c.连接C1、C2，并自C1作C1C2的垂直线C1M。
d.作∠C1C2N=90°-θ，则直线C2N 与C1M 相交于P 点。由三角形的内角和等于180°可知，直角三角形△C1PC2中的∠C1PC2=θ。
e.以C2P 为直径作直角三角形△C1PC2的外接圆，在圆周C1PC2上任选一点A 作为曲柄AB 的机架铰链点，并分别与C1、C2相连。则∠C1AC2=∠C1PC2=θ( 同一圆弧所对的圆周角相等) 。
f.由图2-19 可知，摇杆在两极限位置时曲柄和连杆共线。故有AC1=BC-AB 和AC2=BC +AB。解此两方程可得:
上述均系图上量得长度，故曲柄、连杆和机架的实际长度分别为:
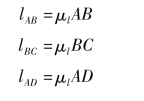
由于A 点可在△C1PC2的外接圆周C1PC2上任选( C1C2及φ 角反向对应的圆弧除外) ，故在满足行程速比系数K 的条件下可有无穷多解。如前所述，A 点位置不同，机构传动角大小也不同。为了获得较好的传力性能，可按最小传动角或其他辅助条件来确定A 点位置。
②曲柄滑块机构:已知曲柄滑块机构的行程速比系数K，冲程H 和偏距e，试设计该曲柄滑块机构。
再作一直线与C1C2平行，使其间的距离等于给定偏距e，则此直线与上述圆弧的交点即为曲柄AB 的机架铰链点A 的位置。当A 点确定后，如前所述，根据机构在极限位置时曲柄与连杆共线的特点，即可求出曲柄的长度lAB及连杆的长度lBC。
(2) 按给定的连杆位置设计四杆机构。
①给定连杆两个位置设计四杆机构:图2-21 所示为铸工车间用的翻台振实式造型机的翻转机构。它是应用一铰链四杆机构A、B、C、D 来实现翻台的两个工作位置的。在图中的实线位置Ⅰ时，沙箱7 的翻台8 在振实台9 上造型振实。当压力油推动活塞6 时，通过连杆5推动摇杆1 摆动，从而将翻台与沙箱转到双点画线位置Ⅱ。然后，托台10 上升接触沙箱并起模。
图2-20 设计曲柄滑块机构
图2-21 翻台振实式造型机的翻转机构
设与翻台固连的连杆2 上两转动副中心间的距离为lBC，且已知连杆的两工作位置B1C1和B2C2，要求设计该四杆机构并确定杆AB、CD、AD 的长度lAB、lCD、lAD。
由已知条件可知，设计此机构的实质在于确定两固定铰链A 和D 的位置。由铰链四杆机构运动可知，连杆上B、C 两点的运动轨迹，分别为以A、D 两点为圆心的两段圆弧，B1B2和C1C2即分别为其弦长。所以，A 和D 必然分别位于B1B2和C1C2的垂直平分线b12和c12上。因此，该机构的设计步骤可归纳如下:
a.根据已知条件，取适当的比例尺μl，绘出连杆2 的两个位置B1C1和B2C2。
b.连接B1、B2和C1、C2并分别作它们的垂直平分线b12和c12。
c.由于A、D 可分别在b12、c12上任选，故实现连杆两位置的设计，可得无穷多组解。一般还应考虑其他辅助条件，例如满足合理的结构要求以及机械在运转中的最小传动角γmin要求等。若本机构中B1C1和B2C2的位置是按直角坐标系给定的，且要求机架上的A、D 两点在x 轴线上，则b12、c12直线与x 轴线的交点即分别为A 和D 点。
d.连AB1C1D 即得所要求的四杆机构。其中lAB=μlAB，lCD=μlC1D，lAD=μlAD。
②给定连杆三个位置设计四杆机构:如图2-22 所示，B1C1、B2C2、B3C3为连杆所要到达的三个位置，要求设计该四杆机构。
图2-22 给定连杆三个位置设计四杆机构
根据已知条件，活动铰链B、C 两点的相对位置已定，所以，设计此四杆机构的实质仍然是要求出两固定铰链点A、D 的位置。由于连杆上的铰链中心B 和C 的轨迹分别为一圆弧，而同时通过要求的三点B1、B2、B3和C1、C2、C3的圆分别只有一个。所以，连架杆的固定铰链中心A和D 只有一个确定的解。即B1B2和B2B3的垂直平分线b12和b23的交点为A 以及C1C2和C2C3的垂直平分线c12和c23的交点为D。连AB1C1D 即为所求的四杆机构在第一个瞬时位置的机构运动简图。
有关纺织机械基础的文章
- 详细阅读
-
平面连杆机构的构造与应用详细阅读
近年来对平面连杆机构的研究，不论从研究范围上还是方法上都有很大进展。已不再局限于单自由度四杆机构的研究，也已开展对多杆多自由度平面连杆机构的研究，并已提出了一些有关这类机构的分析及综合的方法。在连杆机构中，其构件多呈杆状，故常简称构件为杆。若铰链四杆机构中的两个连架杆均为曲柄，则称为双曲柄机构。......
2023-06-26
- 详细阅读
-
梯级链的设计、安全系数和使用寿命计算方法详细阅读
梯级链是自动扶梯最重要的驱动部件，各部件应按无限疲劳寿命进行设计，因此其安全系数最小为5。重载型扶梯一般要求采用安全系数为8的梯级链。梯级链受力计算 梯级链的受力通常需考虑乘客的载荷、梯级链的张紧力及梯级和梯级链自重等，下面介绍一种计算方法。梯级链的使用寿命主要取决于销轴比压，该计算以自动扶梯的制动载荷进行校核。......
2023-06-15
-
刚体在平面的运动方程详细阅读
刚体上与平面Ⅱ相交的部分，称为“平面图形”，用S 表示。根据平面运动的特征，当刚体做平面运动时，平面图形S 上各点始终在平面Ⅱ运动。为研究平面图形S 在其自身平面内的运动，在此平面内建立静坐标系Oxy。式称为“刚体平面运动方程”。......
2023-06-19
-
静定平面桁架内力计算的步骤详细阅读
应用结点法计算桁架内力时，常会遇到一些特殊的结点，可以根据节点的平衡条件判定桁架中某些杆件的轴力为零，或者可以判定与某一结点相连的两杆内力数值相等，从而使计算得以简化。截面法是用适当的截面，截取桁架中包含两个以上结点的部分为隔离体。因此，由平衡条件3.结点法和截面法的联合应用结点法和截面法是计算桁架内力......
2023-08-30
-
平面机构：概述及其运动副分类详细阅读
若组成机构的所有构件都在同一平面或平行平面中运动，则该机构为平面机构。两构件通过面接触而组成的运动副称为低副，通过点或线的形式相接触而组成的运动副称为高副。......
2023-06-26
-
工程地下水：计算承压含水层的导水系数、贮水系详细阅读
它标志含水层在加压下的贮水的能力，或在减压下的释放水的能力。利用非稳定流抽水试验资料，可以计算导水系数T，贮水系数μ＊和压力传导系数a。图2-36s-lg曲线含水层水文地质参数汇总见表2-25。......
2023-09-23
相关推荐