平面任意力系是工程实际中最常见的一种力系,工程计算中的许多实际问题都可以简化为平面任意力系问题来处理。忽略摩擦和自重,当OA 在水平位置、冲压力为F 时系统处于平衡状态。由于曲轮I 承受平面任意力系作用,利用已学过的平面汇交力系平衡和力偶系平衡方程,无法求解力偶矩M 的大小。......
2023-06-19
设平面机构除机架外,共有n 个运动构件,当该机构的各个构件不相互联结构成运动副时,共有3n 个自由度,当各个构件用运动副连接后,由于联结后运动副产生的约束作用,使系统的自由度数目减少。若该机构共有PL个低副,PH个高副,则引入的约束个数为( 2PL+PH) ,即自由度减少(2PL+PH) 个,这时,平面机构的自由度为:
![]()
这个公式就是平面机构自由度的计算公式,式中n 为活动构件数。
例:试计算图示剑杆织机打纬机构和牛头刨床的机构自由度。
解:图2-7( a) 中:F=3n-2PL-PH=3 ×3-2 ×4 =1
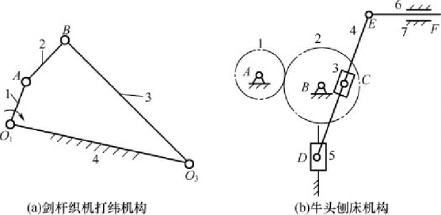
图2-7 机构自由度计算
图2-7( b) 中:F=3n-2PL-PH=3 ×3-2 ×8-1 =1
在应用式( 2-2) 计算平面机构的自由度时,往往会出现计算出的自由度与机构的实际情况不相符合的现象,其原因是还有某些应注意的事项未予以考虑,现将这些注意事项简述如下。
1.局部自由度 在某些机构中,某个构件所产生的相对运动并不影响其他构件的运动,把这种不影响其他构件运动的自由度称为局部自由度。
图2-8( a) 所示的凸轮机构,在按式(2-2) 计算自由度时,
![]()
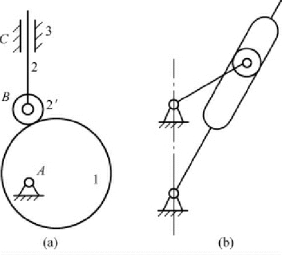
图2-8 局部自由度
但是,实际上并不需要2 个原动件。稍加观察就会发现,滚子2'绕其自身轴线转动的自由度,并不影响其他构件的运动,因而该处是局部自由度。与其相似,图2-8( b) 中的圆滚子也是局部自由度。
对于局部自由度的处理方法是,假想地将滚子2'和构件2 刚性固接在一起,即把2'和2 看做1 个构件,然后按式(2-2) 计算,图2-8( a) 所示凸轮机构的自由度为:
![]()
2.复合铰链 2 个以上的构件在同一处以转动副连接,则构成复合铰链。图2-9( a) 所示就是3 个构件在A 处以转动副连接而构成的复合铰链。而由图2-9( b) 可以清楚地看出,此3个构件共构成2 个转动副,而不是1 个。同理,若由m 个构件( 含机架在内) 在同一处构成转动副( 在机构运动简图上显现为1 个转动副) ,但该处的实际转动副数目为( m-1) 个。在计算机构的自由度时,应注意观察机构运动简图中是否存在复合铰链,以免把转动副的数目搞错。
3.虚约束 对机构运动实际上不起限制作用的约束称为虚约束。
图2-10( a) 实线所示的平行网边形机构,其自由度F =1。若在构件2 和机架4 之间与AB,或CD 平行地铰接一构件5,则不难理解构件5 并没有对机构运动起到实际的限制作用,显然是虚约束。但当按式(2-2) 计算该机构的自由度时,其结果为:
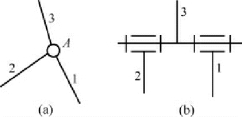
图2-9 复合铰链
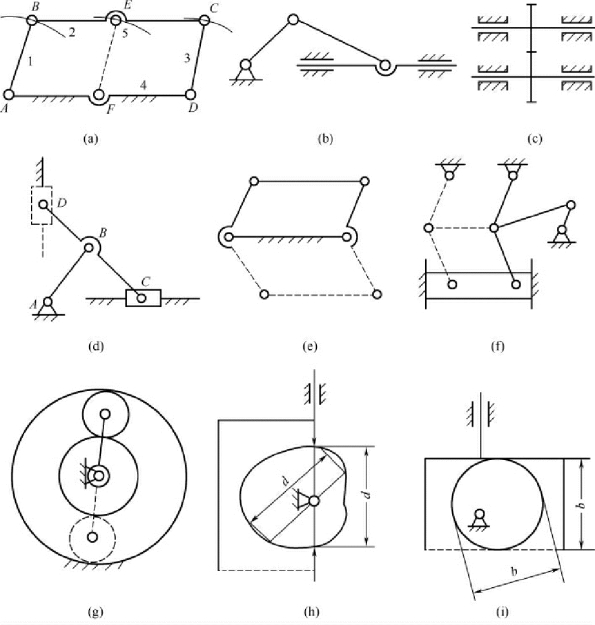
图2-10 虚约束
( a) AB、CD、EF 平行且相等;( b) 平行导路多处移动副;( c) 同轴多处转动副;( d) AB=BC=BD,
且A 是D、C 轨迹交点;( e) 两构件上两点始终等距;( f) 轨迹重合;( g) 相同的多个行星轮;
( h)、( i) 等径、等宽凸轮机构的两处高副
![]()
很明显,以上计算结果与实际情况是不相符的,这说明虚约束会影响使用式(2-2) 计算自由度的正确性。作为处理手段是将机构中构成虚约束的构件连同其所附带的运动副一概扣除不计。
机构中引入虚约束,主要是为了改善机构的受力情况或增加机构的刚度。虚约束类型较多,比较复杂,在自由度计算时要特别注意。为便于判断,将常见的几种形式简述如下。
(1) 若两构件在互相平行的导路上几处接触而组成移动副,则有效约束只有一处,其他处均为虚约束,如图2-10( b) 中的虚线所示。
(2) 若两构件在同一轴线的几处组成转动副,则有效约束只有一处,其他处均为虚约束,如图2-10( c) 中的虚线所示。
(3) 若构件上某点在引入运动副后的轨迹与未引入运动副时的轨迹完全重合,则构成虚约束,如图2-10( d) 中的虚线所示,当AB=BC=CD 成立时,D 处( 或C 处) 为虚约束。
(4) 若两构件上两点间的距离在运动过程中始终保持不变,当用运动副和构件连接该两点时,则构成虚约束,如图2-10( e) 中的虚线所示。
另外,图2-10( f)、( g)、( h)、( i) 所示的虚线部分也是虚约束。
有关纺织机械基础的文章

平面任意力系是工程实际中最常见的一种力系,工程计算中的许多实际问题都可以简化为平面任意力系问题来处理。忽略摩擦和自重,当OA 在水平位置、冲压力为F 时系统处于平衡状态。由于曲轮I 承受平面任意力系作用,利用已学过的平面汇交力系平衡和力偶系平衡方程,无法求解力偶矩M 的大小。......
2023-06-19

静定平面刚架的内力计算同梁一样,仍是用截面法截取隔离体,然后用平衡条件求解。根据荷载情况,将刚架分解成若干杆段,由平衡条件求出杆端内力。该杆上作用有一集中荷载,可以分为CE和EB两个无荷载区段,用截面法求出下列控制截面的弯矩:便可以绘制出该杆弯矩图。根据荷载和已经求出的反力,可以用截面法求出杆件各个控制截面的剪力和轴力,从而绘制出整个钢架的剪力图和轴力图,如图12-18、所示。......
2023-06-16

近年来对平面连杆机构的研究,不论从研究范围上还是方法上都有很大进展。已不再局限于单自由度四杆机构的研究,也已开展对多杆多自由度平面连杆机构的研究,并已提出了一些有关这类机构的分析及综合的方法。在连杆机构中,其构件多呈杆状,故常简称构件为杆。若铰链四杆机构中的两个连架杆均为曲柄,则称为双曲柄机构。......
2023-06-26

平面汇交力系可以建立两个独立的平衡方程,解算两个未知量。继续取8、6、7等结点为隔离体,可求得桁架右半边各杆的内力。图12-30桁架轴力示意在桁架内力计算时,往往会遇到内力为零的杆件,这种杆件称为零杆。计算桁架的内力宜从几何分析入手,以便选择适当的计算方法,灵活地选取隔离体和平衡方程。除结点法外,计算桁架内力的另一基本方法是截面法。截面法适用于联合桁架的计算以及简单桁架中求少数指定杆件内力的情况。......
2023-06-16

杆件轴线及荷载作用线均处在同一平面内的刚架,称为平面刚架。在工程中实际应用的刚架,多数是超静定的,静定刚架较少采用。图3-112.静定平面刚架计算静定刚架的内力通常有弯矩、剪力和轴力,其计算方法原则上与静定梁的计算相同。......
2023-08-30

故一个链杆能使体系减少一个自由度,相当于一个约束。在图 2-6 中,平面内点 A 原有 2 个自由度,若用两根不共线链杆 1、2 将其与基础相连,则 A 点的位置被完全确定,体系的自由度为零。此时,若再加一根链杆 3,体系的自由度仍为零,这说明所增加链杆约束的作用与体系中已有约束中的作用是重复的。如图 2-6 所示体系中和三根链杆中的任意两根均可认为是必要约束,则剩余的一根为多余约束。......
2023-08-30

同时具备这三个特征的称为机器,仅具备前两个特征的称为机构。如图4-1 所示的内燃机由活塞、连杆、曲轴、齿轮、凸轮、顶杆及气缸体等组成,它们构成了连杆机构、齿轮机构和凸轮机构,如图4-2所示。内燃机的功能是将燃料的热能转化为曲轴转动的机械能,其中连杆机构将燃料燃烧时体积迅速膨胀而使活塞产生的直线移动转化为曲轴的转动;凸轮机构用来控制适时启闭进气阀和排气阀;齿轮机构保证进、排气阀与活塞之间形成协调动作。......
2023-06-26

平面连杆机构是所有机构全部用低副连接而成的平面机构,又称平面低副机构。因而,平面连杆机构在各种机械和仪器中获得了广泛使用。平面连杆机构中最常见的是由四个构件组成的四杆机构。其中,AD为机架,与机架相连的杆AB、CD称为连架杆。平面连杆机构的结构和维护平面连杆机构是面接触的低副机构,低副中的间隙会引起运动误差,所以要注意保证良好的润滑以减少摩擦、磨损。......
2023-06-23
相关推荐