使用选择属性评估差分序列对行为识别的影响：基于HMM模型的实验分析

2025-09-29 理论教育版权反馈

【摘要】：图6.7HMM模型训练与利用H MM进行识别的流程图2.利用选择属性来测试各特征的贡献Weizmann行为数据库中包含90个视频。以差分序列为例，获取的差分序列中包含15个差分的图像。最终，获得的特征数据是31×15的序列，称差分序列的原始全特征序列。如图6.10所示的16个精度，12个基于差分序列的数据测试精度高于基于全前景序列的数据测试精度。

1.建模与识别

马尔可夫链是一种描述时间序列变化规律的随机过程。它的限定条件是历史有限性，也就是当前状态只与前一个状态有关。隐马尔可夫模型HMM是一个符合包含隐含状态的马尔可夫链的统计模型。尽管人的运动不完全符合历史有限性，但很多研究都表明人的行为可以由HMM有效建模[163，164，176]。

一个HMM是5元组：μ=（S，O，∏，A，B）。其中，S和O是状态集合和观察集合，∏是初始状态矩阵，A是状态之间的转换概率矩阵，B是从状态到观察的转换矩阵。利用具有同一行为标签的一组观察，通过最大化概率P（O|μ）可以获得模型μ。利用各行为的观察数据学习得到的模型表示为{μ1，μ2，…，μi，…}。一个新的、没有行为标签的观察，计算它与各个HMM模型的似然度，将它分类为最大似然的类别，就是argmax P（O|μi）。利用HMM进行训练和识别行为的流程如图6.7所示。

本章和第7章中HMM的训练和识别利用的是Kevin Murphy的贝叶斯工具，其中包含了HMM的训练和似然度计算模块[176，177]。

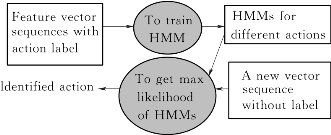
pagenumber_ebook=95,pagenumber_book=90

图6.7　HMM模型训练与利用H MM进行识别的流程图

2.利用选择属性来测试各特征的贡献

Weizmann行为数据库中包含90个视频。每个视频又被划分为视频段。大家都希望在尽量短的视频段中可以识别行为。经过实验测试，15帧一段视频足够获取好的识别效果。当然，是针对这个视频帧速和本章利用的特征与建模方法来讲的。以差分序列为例，获取的差分序列中包含15个差分的图像。之后，前述的特征被提取，获得15长度的特征序列。在计算差分序列时，连续3帧或更多没有运动的帧被忽略掉，因为没有运动的帧就意味着差分图像中没有前景，也就没有特征可以提取。最终，获得的特征数据是31×15的序列，称差分序列的原始全特征序列。从全前景序列中提取的特征数据仍是31×15的序列，称全前景序列的原始全特征序列。作为比较，以下的测试将分别在这两类特征序列上进行。

测试利用留一策略（leave-one-out）：对于一种行为的特征序列集，随机抽取一个序列作为测试序列；利用其他的序列进行HMM训练，获得HMM模型；利用获得的模型对保留的测试序列进行测试；这个过程进行多次，计算测试精度。在HMM中，利用高斯混合模型来规划观察，因为特征是连续值。测试中，隐藏状态设为2个，高斯混合模型设为3个。这两个参数有变动时，测试精度有少量改变。每次测试为10个行为中的每个行为保留一特征序列作为测试序列，另外的序列用来训练HMM。之后，对保留的10个序列进行测试，计算识别精度。

为了测试前述特征集中不同特征对行为识别的贡献程度，也为了对比从全前景序列中提取的特征数据与从差分序列中提取的特征数据对不同行为识别的效果，从两套原始全特征序列中进行了组合型特征选择，形成特征子集。利用两套特征子集进行行为识别测试，测试结果对比显示如图6.8和图6.9所示。其中，x轴表示选择的特征子集的构成，y轴表示利用相应子集测试后的精度对比。图中的每个精度值均为30次测试的平均精度，精度值的标注是百分比重。从两图中可以看出最高的识别精度达到了98%。并且有：

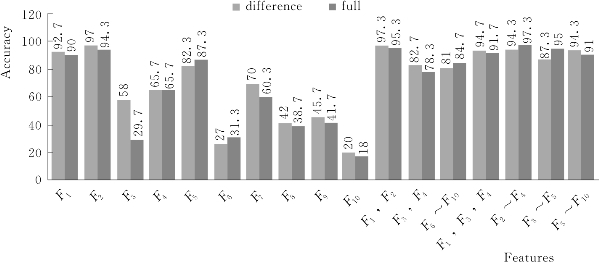
pagenumber_ebook=96,pagenumber_book=91

图6.8　从两个数据来源的特征数据对行为识别的贡献对比（1）

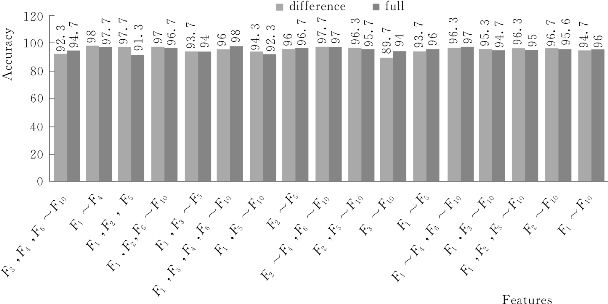
pagenumber_ebook=96,pagenumber_book=91

图6.9　从两个数据来源的特征数据对行为识别的贡献对比（2）

（1）对于单项特征，F1和F2对行为识别效果最好，表明具有方向的外观特征能更好地表征姿态。Hu矩（F5）也可以表达形状，但是它们是对位置、伸缩及旋转不变的，也就是说这些特征丢失了，所以只用Hu矩来识别行为效果不好。F3、F4、F6～F10也可以表达形状，但是每个特征只表达了形状的一些方面，单独使用效果不好。

（2）通过联合使用多种特征，精度普遍提高了。应该说每种特征都对行为识别有贡献，但不是特征用得越多识别效果越好，联合全部特征并不能获得最好的精度。例如，差分序列中F2联合F3和F4后比只利用F2的精度更低了。在一定程度上，F6～F10与F1～F2表达的信息有重叠，而F3～F4表达的信息与F1～F2所表达的信息很不同。因此，可以看到联合F1～F4效果要好于F1～F2与F6～F10的联合。

（3）特别说明，在10个单独特征中，有7个来源于差分序列的数据识别能力高于来源于全景序列的数据；在24个联合特征中，13个来源于差分序列的数据识别能力高于来源于全景序列的数据。这个结果表明，差分序列中包含的识别行为的信息多于或者不少于全景序列中的信息。

3.通过投票识别行为

为了提高测试效果，又进行了投票方法的测试。考虑投票方法有两个原因：(https://www.chuimin.cn)

（1）前述特征集中的所有特征均对行为识别有效。

（2）单纯联合更多的特征并不能提高识别精度。

根据选择测试的结果，将前述特征组成5个群（feature groups，FGs）。每个群有一个投票权重，权重值来源于组合测试中的精度。这些特征群如下：

FG1-F1，在差分序列特征中权重是92.7%，全景序列中权重是90%。

FG2-F2，在差分序列特征中权重是97%，全景序列中权重是94.3%。

FG3-F3、F4，在差分序列特征中权重是82.7%，全景序列中权重是78.3%。

FG4-F5，在差分序列特征中权重是82.3%，全景序列中权重是87.3%。

FG5、F6～F10，在差分序列特征中权重是81%，全景序列中权重是84.7%。

测试仍遵循留一测试。利用FG集训练HMM，留下的序列用于测试。每个FG的投票有自己的权重，测试序列最终被判定为得票加权权重最大的行为类别。如图6.10所示显示了FG投票测试的结果。图中每个精度是30次测试的平均值。

将图6.10与图6.8和图6.9对比，对于来源于差分序列的数据，16个精度中，9个投票方法获得的精度高于对应的组合方法获得的精度；对于来源于全景序列的数据，16个精度中，12个投票方法获得的精度高于对应的组合方法获得的精度。如图6.10所示的16个精度，12个基于差分序列的数据测试精度高于基于全前景序列的数据测试精度。

FG1、FG2和FG4基于差分序列特征数据识别精度均达到98%。如图6.11所示中显示了这个测试的混淆矩阵，以进一步观察识别效果。可以看到，其中running、jumping sideways、skipping和walking有些混淆。观察这些行为的差分序列，可以看到它们确是相似的。

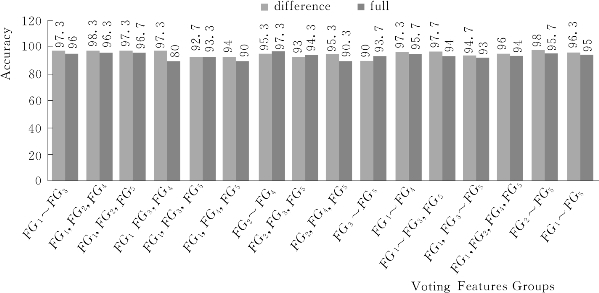
pagenumber_ebook=98,pagenumber_book=93

图6.10　来源于两种序列的特征群投票识别行为结果对比

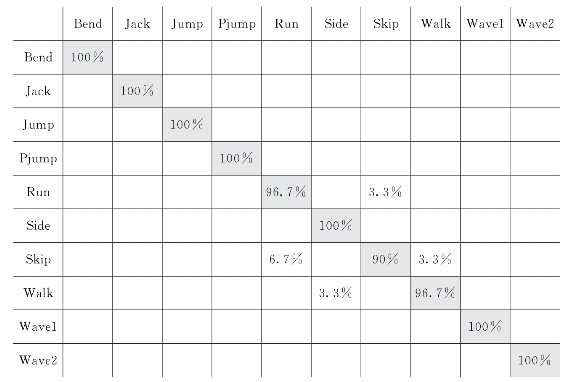
pagenumber_ebook=98,pagenumber_book=93

图6.11　FG1，FG2和FG4投票方法运动30次获取的混淆矩阵

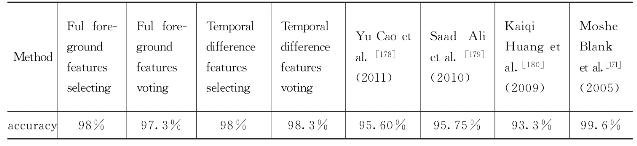
将本章的工作效果与近期的一些研究结果进行比较，如表6.1所示。表中的测试数据均来源于Weizmann行为数据库。可以看到，Blank等人的工作识别精度很高，他们的方法提取数据时需解Poisson等式，这个过程很耗时。从数字上讲，本章方法的识别精度与现时流行方法精度相当，而且只利用了差分序列三方面表观特征即可获取精度98.3%，这与其他方法比较，有一定优势。

表6.1　本章方法的识别精度与近期工作中方法的识别精度对比

pagenumber_ebook=99,pagenumber_book=94

本章方法利用Matlab实现。所用的计算机处理器频率是2.26GHz，内存12GB。以从差分序列提取特征为例，从Jumping行为包含72帧、播放时间是2.88s的一段视频中提取特征数据需4.84s，包括计算差分图像和提取31个特征值。因此，处理1帧的平均时间约为0.067s。在FG1、FG2和FG4投票方法中，利用HMM识别一个序列中的行为需0.049s。由此可以说本章的方法达到了实时识别。

使用选择属性评估差分序列对行为识别的影响：基于HMM模型的实验分析

相关推荐