multcomp包中的cholesterol数据集,有50个患者均接受降低胆固醇药物治疗五种方法对患者的效果.五种方法分别是:20 mg一天一次、10 mg一天两次和5 mg一天四次,其中前三种所用药物相同,剩下的drugD 和drugE是候选药物.哪种药物疗法降低胆固醇最多?......
2023-11-18
前述测试主要是对利用特征数据进行分类精度对比,由于数据集大小、类分布不同等因素影响,精度只能在一定程度上代表数据对分类的支持情况。为探索特征数据的性能,更深入的分析是必要的。作为分类的特征数据,希望其类间距离大而类内方差小,也就是说,不同类别间的特征值距离较远,而同一类别内的特征距离较近。为分析特征数据的距离特性,分别进行了判别式分析和特异分析。
1.判别式分析
为衡量特征数据间的距离,常规的就是利用欧氏距离,欧氏距离也适合本节数据集的计算。鉴于第5.3.5节的分类方法中,线性判别式分类器分类精度较好,选择利用此分类器中的线性判别式来计算数据集的距离特征。前面的实验表明,在区间划分取10行×10列以上时,可以获得较好的精度,为了不增加计算的复杂度,选择10×10划分的数据集,按6类数据规模大致相同的比例,组成一组新数据集,其记录构成为:walking-36、running-40、jogging-40、handwaving-40、handclapping-40、boxing-40,数据集大小为236×84。利用SPSS将集合进行判别式分析,分析以全部84维向量为独立的变量,建立Fisher线性的判别式,并根据判别函数来计算各类间距离与类内距离。
基本的Fisher判别方法是一种两类别判别方法,它利用使Fisher准则达到最大值的方向作为最优投影方向,样本模式在该方向投影后的类间散度达到最大而类内散度达到最小。以投影函数作为判决函数function,当样本的function的得值大于某个阈值时判定为一类,否则判定为另一类。判决阈值f0的典型选择有3种[94]:
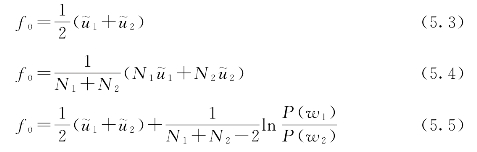
式中:![]() 为function作用在第1类和第2类样本上的平均值;N1、N2为第1类和第2类样本的数量;P(w1)、P(w2)为第1类和第2类样本先验概率。
为function作用在第1类和第2类样本上的平均值;N1、N2为第1类和第2类样本的数量;P(w1)、P(w2)为第1类和第2类样本先验概率。
对于多类的判别问题,以一类为判别目标,其他样本均设定为另一类,可以构造一判别函数;在剩余的类中,再以一类为判别目标,其他样本均设定为另一类,构造第2个判别函数;重复此过程,一直到每一类均能判别。所以一般n类分类问题需构造n-1个判别函数。
利用一Fisher判别函数,可以计算出每个记录的得值y。如果将记录数为n的数据集按其类别分为k组,第i组的记录数为ni,那么所在组间距离的平方和也称为组间散度,用式(5.6)表示:

式中: 为全部数据的判别式得值的平均值;
为全部数据的判别式得值的平均值;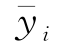 为第i组数据得值的平均值。
为第i组数据得值的平均值。
可见,SSA是各组平均值与总体平均值离差的平方和,反映了组间的总距离。SSE则反映了组内离差平方和,也称组内散度,其计算方法如式(5.7)所示:

F则是平均组间平方和与平均组内平方和之比,其值可有效表征数据集中组间松散与组内紧密的对比,计算方法如式(5.8)所示:

式(5.8)的F服从(k-1,n-k)个自由度的F分布,根据F分布表可以计算出其相伴概率值。如果相伴概率值小于显著性水平a,则认为各组间总体均值有显著差异[151]。
因为数据集中有6类数据,建立了5个判别式Function 1~Function 5,由各判别式的Structure Matrix可知,特征向量的不同分量与不同的Function显著相关,各判别式的特征值如表5.9所示。
表5.9 5个判别式的特征值
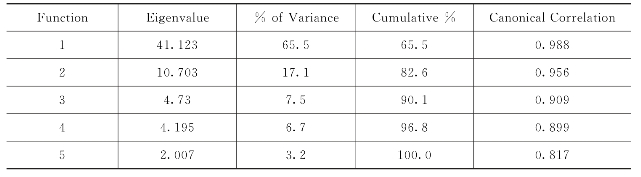
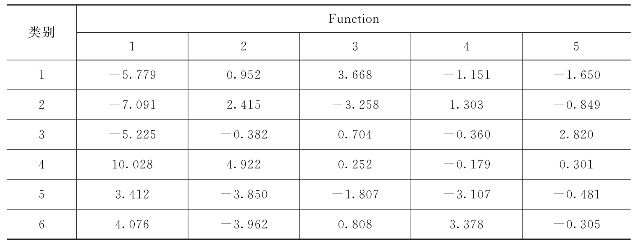
其中的特征值Eigenvalue即为式(5.5)中的F值,表5.9的第1行表示利用Function 1,计算出的F值为41.123,它对整体分类的贡献是65.5%,下一列是累计的贡献百分比,最后一列为典型相关系数,反映的是此判别函数与组别间的关联程度。可以看出5个判别式累计分类的贡献率是100%,与分类类别相关程度均大于0.8;由Structure Matrix可知,数据集中的84维特征分别与5个判别式函数达到相关性显著水平;表5.10中1~6类代表前述的6类行为:walking、running、jogging、handwaving、handclapping、boxing,各类数据在不同的判别式的中心有显著差距,说明5个判别式对此数据集的分类判别是有效的。
表5.10 各类记录在5个判别式上的中心
如图5.6所示显示出由Function 1和Function 2计算出的各类数据的分布情况,其中,handwaving类别(4),已经能有效区分,但其他类别还要进一步识别。
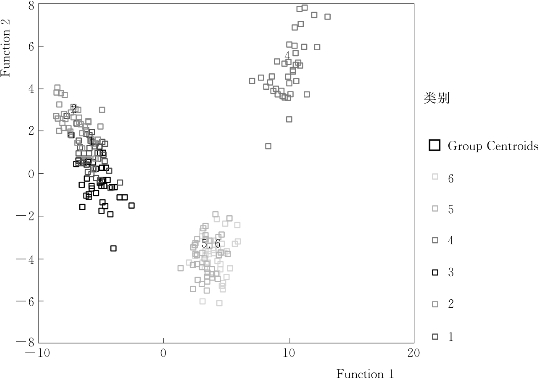
图5.6 由Function 1和Function 2计算的各类数据分布图
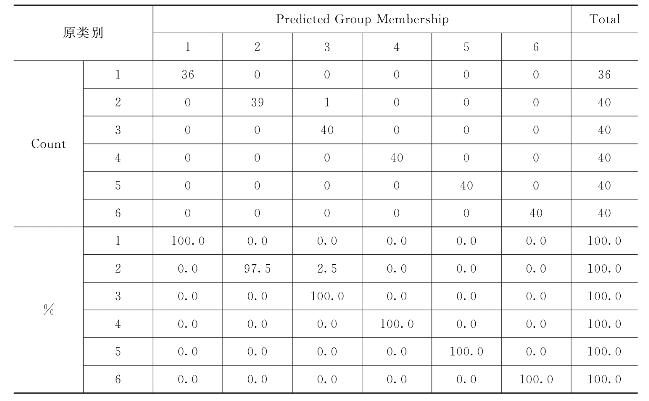
如表5.11所示列出了最终的分类结果,可以看出分类错误仍出现在running和jogging之间,这和前面的测试是一致的。
这组分析表明,特征数据集具有较好的线性可分特性。
表5.11 Fisher线性判别的分类结果
2.特异分析
在数据集中,一些数据或对象与其中其他数据或对象显著不同,则称是特异数据或特异对象。同一类特征数据相似性高,而不同类数据相似性低,在一类数据中掺入少量的其他类数据,希望掺入的数据能被识别为特异的。选择10×10划分的数据集,构造4个子集如表5.12所示,其中每个子集均有一大类,另外的类别记录加一起为小类,约占总记录的10%。
表5.12 4个子集组成表

以4个子集为数据,以大类为正类,以小类为负类,利用本书第3.2节的全局特异数据挖掘算法,计算记录的特异因子,将其排序后绘制ROC图,结果如图5.7和图5.8所示,各ROC曲线下面积值如表5.13所示。
表5.13 各ROC曲线下面积

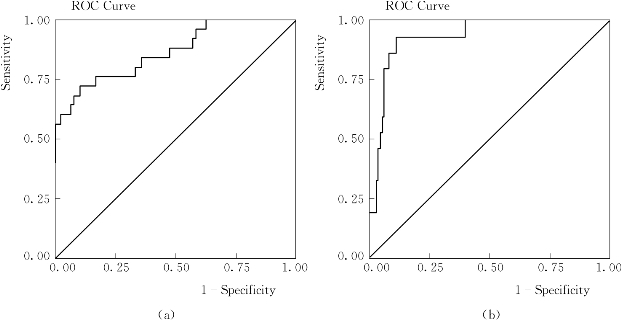
图5.7 Subt1和Subt2的特异因子ROC图
(a)Subt1;(b)Subt2
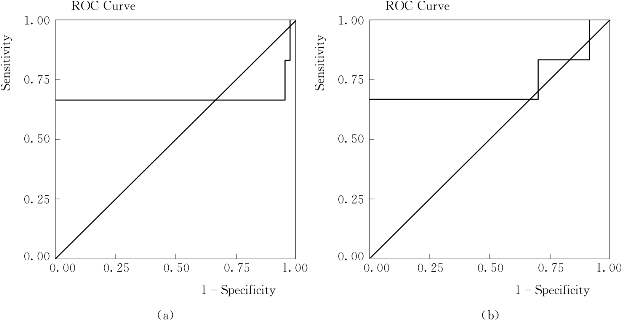
图5.8 Subt3和Subt4的特异因子ROC图
(a)Subt3;(b)Subt4
由以上的图表可反映出,小类数据均表现出了较好的特异性。在Subt3的ROC曲线性能是最差的,主要原因是其中涉及running和jogging的区分。
至此,本节提出的行为识别特征数据具有较好的“不同类别间的特征值距离较远,而同一类别内的特征距离较近”的特性。
有关数据挖掘算法及在视频分析中的应用的文章

multcomp包中的cholesterol数据集,有50个患者均接受降低胆固醇药物治疗五种方法对患者的效果.五种方法分别是:20 mg一天一次、10 mg一天两次和5 mg一天四次,其中前三种所用药物相同,剩下的drugD 和drugE是候选药物.哪种药物疗法降低胆固醇最多?......
2023-11-18

焊接方法的种类很多,新的分类方法又不断出现,为此对焊接方法进行科学的分类很有必要。再把各种焊接方法所具有的两个特征列入表内的某一坐标位置。其优点是可根据分类图直接了解某一焊接方法的某些特征,也可根据这两个特征将某个焊接方法归入图中的某一位置,它属“开放型”分类法,适应性强。在实际中,往往称呼某种焊接方法的全名,如二氧化碳气体保护焊、脉冲闪光对焊等。表0-1 二元坐标法—焊接方法分类......
2023-06-25

在实验2.3.2中曾对iris数据集进行描述和展示,在实验2.3.4中曾对iris数据集进行可视化.以下将对iris数据集进行进行聚类分析.根据实验2.3.4,我们只知道数据集内有三个品种鸢尾花而不知道每朵花的真正分类,只能凭借花萼及花瓣的长度和宽度分类.以下对鸢尾花iris数据集进行聚类分析,代码如下:>data(iris);attach(iris)>iris.hc1<-hclust(dist(......
2023-11-18

本节在Hadoop平台上提出了一种基于MapReduce编程思想设计与优化的KMeans并行算法。图5-43KMeans聚类运行结果图5-43是KMeans聚类运行结果,运行结果的上半部分是得到的16类簇的聚类中心,如表5-13所示;下半部分是对452条数据的聚类结果,聚类结果中的数字1~16表示聚类的标签,如表5-5所示。整理统计KMeans聚类运行结果,如表5-14所示。本节在进行基于Hadoop的医学数据聚类算法研究时,以心律失常数据作为实验数据集,利用KMeans聚类算法在Hadoop平台上实现算法。......
2023-11-08

为了获得这些软弱结构面的抗渗强度,中国电建集团中南勘测设计研究院有限公司采用多种试验方法进行了试验研究,经综合分析后得到的软弱结构面抗渗强度指标为:坝基岩体层间夹层的临界水力梯度为5.35,破坏水力梯度为33.79;挤压破碎带临界水力梯度为15.91,破坏水力梯度为48.66。因此,从工程安全及经济性角度综合出发,左非3坝基软弱夹层抗渗透变形破坏的水力梯度确定为30.0。......
2023-06-28

图4-3是集热管热损分析图。根据热损分析图可列出以下能量平衡方程:图4-3 集热管热损分析图1—换热流体 2—吸热管内壁 3—吸热管外壁 4—玻璃套管内壁 5—玻璃套管外壁 6—周围环境 7—大气环境 8—集热管支架1)金属吸收管内壁能量平衡方程:Q12,conv=Q34,cond;2)金属吸收管外壁能量平衡方程:Qsolarabs=Q12,cond+Qcondbracket+Q34,rad+Q34,conv;3)玻璃套管内壁能量平衡方程:Q45,cond=Q34,rad+Q34,conv;4)玻璃套管外壁能量平衡方程:Q45,cond+Q5,abs=Q56,conv+Q57,rad。......
2023-06-23

MASS包中包含Boston数据集(波士顿房价),它记录了波士顿周围506个街区的medv(房价中位数).我们将设法用13个预测变量如rm(每栋住宅的平均房间数),age(平均房龄),lstat(社会经济地位低的家庭所占比例)等来预测medv(房价中位数).(1)首先查看Boston数据集(波士顿房价)中的变量>library(MASS)>fix(Boston)>names(Boston)结果如下......
2023-11-18
相关推荐