PCP每次均将数据集随机分成2个子集，轮流作为训练集与测试集，得到2个测试精度，10次均值实际上是20个精度值的平均，这个均值的有效性更好。交叉检验实验说明，利用特征数据能较好地区分各类行为。按第5.3.2节向量分量排列顺序，分量下标为k的特征，如果k或k+1能被4整除，说明其反映的是空档变化情况；不符合这个特征，说明其反映的是宽度变化情况。......
2023-06-16
双向置信测试对不平衡数据集分类的优化
【摘要】：针对不平衡数据集的分类问题是一类重要的分类问题，在网络入侵检测、信用卡欺诈识别及疾病诊断等领域有实际应用。表4.6中显示的是整个数据集的分类精度，在不平衡数据集中，小类是被关注的对象，其被识别的精度更能反映算法的性能判别。在4个数据子集Sub1、Sub2、Sub3、Sub4中，包含8个攻击类和一个正常类。图4.24个子集的规模与训练时间的关系图4.34个子集的规模与测试时间的关系
针对不平衡数据集的分类问题是一类重要的分类问题，在网络入侵检测、信用卡欺诈识别及疾病诊断等领域有实际应用。这类问题的数据分析有3个层面：
（1）在不平衡数据集中识别出稀有类记录。例如，在网络访问数据集中识别出攻击记录，这类记录一般占很小的比例（如低于10%），称为稀有类。这一层面的问题一般称稀有数据挖掘问题，其挖掘方法一般是基于距离或密度的，如本书第3章所述。
（2）已知某记录是稀有类记录，识别出其属于稀有类中的哪一类。例如，在网络访问数据集KDDCUP99中，正常访问记录是大类，攻击记录是稀有类，攻击记录又分为22个类。已经知道某记录是攻击记录，识别它是哪类攻击是第二个层面问题。
（3）在不平衡数据集中识别出大类和稀有类，并识别出稀有类的类别。可以看出这3个层次是逐次深入的，第3.4.4节的方法和测试是针对第三个层面的。
当然稀有数据挖掘算法能有效，说明不平衡数据集中稀有记录的属性确有异常的表现。仔细分析KDDCUP99数据集，可以发现其中的攻击记录属性具有特异性，并且不同类的攻击记录其特异属性有明显差距。基于这一事实，并考虑到不平衡数据集中起决定作用的是稀有属性（支持度小于等于指定阈值的属性）；一记录被判定不是某个攻击类，那么它就是正常类，因此对第3.4.2节的实验方法进行了以下修改：
（1）设置一支持度阈值，如10%，在生成规则集时只采集前件支持度≤10%，并且满足两置信度要求的规则，不采集正常类的规则。
（2）在测试时，t仍被判定属于得分最高的类。由于不采集正常类的规则，只要最高得分＞0，就判定是攻击类，当所有攻击类得分均小于等于0时，判定t为正常类。
1.识别精度测试
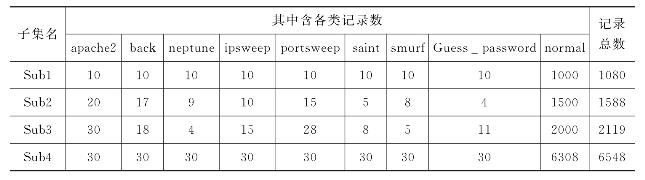
KDDCUP99是网络访问记录数据集，每行数据记录了一次网络访问的属性及访问类别。访问类别反映了本次访问的性质，属于典型的不平衡数据集，其中大部分记录属正常访问类（normal），称为大类，例如＞90%。另外的类别均属于攻击类，称为小类。我们从KDDCUP99中选择了corrected数据集，corrected数据集共有65536条记录。从中选择了正常类记录和8类攻击记录组成4个数据子集，Sub1、Sub2、Sub3、Sub4，其记录构成如表4.5所示。各子集中攻击记录的比例均＜10%，Sub1和Sub4中攻击类记录是均匀的，Sub2和Sub3中攻击类记录是非均匀的。
表4.5 4个子集的记录构成
设置支持度阈值为10%，充分置信度阈值为50%，必要置信度阈值为80%。分别以各子集为训练集和测试集，进行实验，结果如表4.6所示。表中错判记录数由3列合计得到，“攻-攻”表示其中攻击记录被错判为另一类攻击的记录数，“攻-正”表示其中攻击记录被错判为正常类的记录数，“正-攻”表示其中正常记录被错判为攻击类的记录数。
表4.6 KDDCUP99数据集上的测试结果
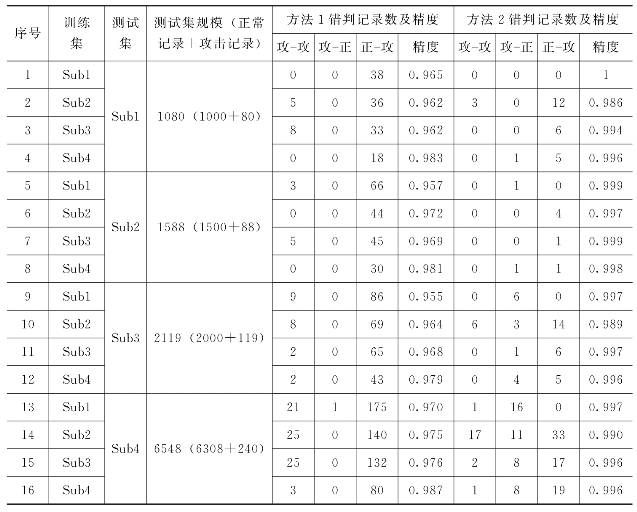
由表4.6，所有测试结果中方法2的精度均高于方法1的精度，方法2的精度非常高；从4项一组的实验中可以看出训练集的规模、训练集中小类记录的均衡程度对测试结果影响较小；由于不采集大类的规则，实验中生成的规则集R规模较小。
表4.6中显示的是整个数据集的分类精度，在不平衡数据集中，小类是被关注的对象，其被识别的精度更能反映算法的性能判别。表4.7反映的是以Sub1为训练集时，Sub2测试结果中每个攻击类的正确率P、召回率R和F 1值，其中对比了方法1与方法2的值。P、R和F 1计算公式如下：
表4.7 Sub2测试中各攻击类的P、R与F 1值对比
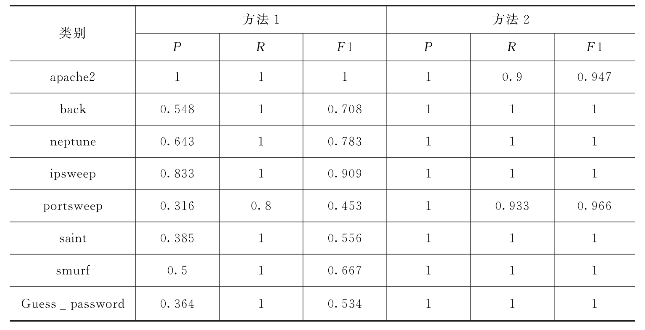
由表4.7，在适当利用必要规则置信度后，P、R和F 1的值均得到了显著提高。
2.ROC曲线分析
本实验中，方法1与方法2判定一记录类别时，均依据量化的得分值。在4个数据子集Sub1、Sub2、Sub3、Sub4中，包含8个攻击类和一个正常类。如果以一个攻击类为正类，其他攻击类和正常类为负类。那么，据量化的得分绘制ROC曲线，可以有效表征两方法的分类效果，从而说明必要置信对分类的贡献。仍以Sub1为训练集，以Sub2测试结果中portsweep攻击类的方法1与方法2得分为数据，绘制ROC曲线，如图4.1所示，其曲线下面积的对比如表4.8所示。
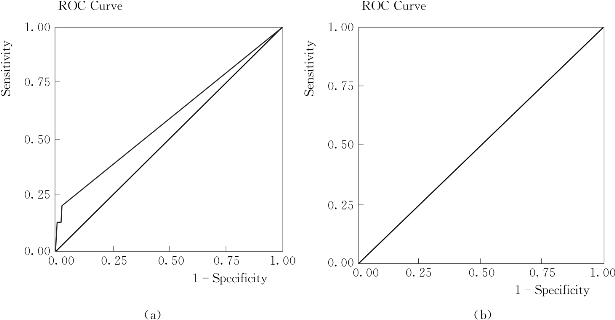
图4.1 portsweep类在测试中得分的ROC图
（a）方法1；（b）方法2
表4.8 portsweep类测试得分ROC曲线下面积
由图4.1和表4.8可知，必要规则置信度对portsweep类的识别有显著贡献。
3.时间效率分析
本实验方法的训练过程只需访问两次训练集，其时间复杂度为O（N），N是训练集规模。测试过程，方法1与方法2均需访问一次测试集，对测试集中的每个记录，需与规则集的每个规则匹配，其时间复杂度是为O（KN），其中K是规则集中规则的数目，N是测试集的规模。在实验中也验证了这一点，不同规模数据集的训练时间、对应方法2的测试时间如图4.2和图4.3所示。
图4.2 4个子集的规模与训练时间的关系
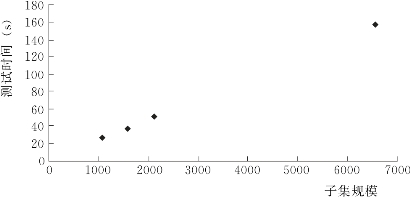
图4.3 4个子集的规模与测试时间的关系
有关数据挖掘算法及在视频分析中的应用的文章
- 详细阅读
-
特征数据集其他分类性能分析测试方法及结果分析详细阅读
前述测试主要是对利用特征数据进行分类精度对比，由于数据集大小、类分布不同等因素影响，精度只能在一定程度上代表数据对分类的支持情况。为探索特征数据的性能，更深入的分析是必要的。这组分析表明，特征数据集具有较好的线性可分特性。表5.11Fisher线性判别的分类结果2.特异分析在数据集中，一些数据或对象与其中其他数据或对象显著不同，则称是特异数据或特异对象。......
2023-06-16
-
数据分区与分类的优化方法详细阅读
图7-41 FANUC系统的存储空间和储能电容2.数据的分类机床数据文件主要分为系统文件、机床厂文件和用户文件三种。其中，系统文件为FANUC公司提供的CNC控制软件和伺服控制软件等；MTB文件包括PMC程序等；用户文件包括CNC参数、PMC参数、螺距误差补偿值、用户宏程序变量、刀具补偿值、加工程序、对话式编程数据、操作履历数据及伺服波形诊断数据等。表7-6 FANUC系统FROM中的文件注：□表示1个字符的数字，表示1个字符的字母或数字。......
2023-06-23
-
R实验：对smoke数据集进行对应分析详细阅读
以下对smoke数据集进行对应分析．（1）首先查看smoke数据集的信息＞library(ca)＞data(＂smoke＂)＞smoke结果如下：这个数据集来自Greenacre（1984），被应用于多个统计软件作为对应分析的说明案例数据．它的内容是一个5行（阶层：SM，JM，SE，JE和SC）4列（吸烟习惯：none，light，medium 和heavy）的列联表，给出了一个虚构的公司内各阶层......
2023-11-18
-
Boston数据集的回归分析详细阅读
MASS包中包含Boston数据集（波士顿房价），它记录了波士顿周围506个街区的medv（房价中位数）．我们将设法用13个预测变量如rm（每栋住宅的平均房间数），age（平均房龄），lstat（社会经济地位低的家庭所占比例）等来预测medv（房价中位数）．（1）首先查看Boston数据集（波士顿房价）中的变量＞library(MASS)＞fix(Boston)＞names(Boston)结果如下......
2023-11-18
-
在KDDCUP99数据集上的实验结果优化方案详细阅读
KDDCUP99数据集是网络访问数据记录集[117]，它包含了若干个数据集，本书选用的是corrected.gz。每个记录有42个属性，前41个是访问特征属性，最后一个属性是记录的类别标识。从corrected中按比例分别选择两类记录来构造若干子集，其中攻击记录所占比例均小于10%，以使其为特异记录。分别在30+300、50+500、100+1000、200+2000、300+3000共5个子集上分别运行PecuFind算法程序和CpecuFind算法程序。很明显，Cpecu Find发现攻击记录的能力强于Pecu Find。表3.330+300和50+500上的实验结果比较......
2023-06-16
-
验证网络性能：如何对网络进行测试和优化详细阅读
图9-29实验测试平台和演示器设置PU和OFP代理是在VMware ESXi V5.1创建的虚拟机阵列上实现的，VMware ESXi V5.1运行在IBM X3650服务器上。如图9-30和图9-30所示，10.108.67.21、10.108.50.74和10.108.49.14分别表示RC、PC和OC的IP地址，而10.108.49.23和10.108.49.24分别表示相关的OF-BVOS的IP地址。特征请求消息负责通过定期查询BVOS来监视当前状态。在完成RIP后，OC和RC提供SP，并通过流修改消息分配射频来控制相应的节点。图9-30MDRI的消息序列的Wireshark捕获......
2023-06-19
-
利用WisconsinBreastCance详细阅读
Wisconsin Breast Cancer数据集有699条记录，每条记录都是记录一位胸部有肿瘤的病人的特征数据。可以从中随机选择444条良性记录和39条恶性记录组成一数据集。文献[107]描述的是基于聚类的且基于密度局部特异数据挖掘方法—FindCBLOF，在Wisconsin Breast Cancer Data上的实验结果显示了其挖掘特异数据的能力在同类算法中是优越的。结果再次表明Cpecu Find挖掘特异数据的能力略优于pecu Find。表3.4Wisconsin Breast Cancer数据集上的实验结果比较......
2023-06-16
相关推荐