以属性层次为讨论依据，Zhong Ning的算法时间复杂度明显是O（N2），其中N是属性集合中的数据数目。对于本书提出的算法，设经聚类后，聚类的个数为k；经计算聚类的CPF后，需以数据单独参加PF值计算的数据个数与以类整体参加PF值计算的类的个数之和为n。在聚类阶段，采用的聚类算法时间复杂度是线性的，为O（N）；聚类后计算每个聚类的CPF值阶段时间复杂度是O（k）；最后计算PF阶段的时间复杂度是O（n2）。其中，最后阶段的时间复杂度是平方级的，希望n与N的比值很小，最好与N的增长保持线性以下的增长速度。在第3.3.2小节的数据集30+300、50+500、100+1000、200+2000、300+3000上运行Cpecu Find算法程序，λ取10%，采集在运行过程中n与N的关系，得到图3.4。其中，A17、A18、A19 3条曲线显示的是在数据集中第17、第18、第19个属性集在实验中n随N变化的情况，作为对比，直线10%显示的是n与N比值为10%的直线。
由图3.4可知，n与N的比值会在给定λ周围变化。因不同属性的数据集特征不同，聚类结果不同，n的变化没有统一的规律。由于特异挖掘中λ值很小，提出的算法具有较好的可扩展性。
仍采用在第3.3.2小节的渐增数据集30+300、50+500、100+1000、200+2000、300+3000，在其上分别运行PecuFind算法和CpecuFind算法。在Cpecu Find算法程序中，λ取10%。如图3.5所示显示出了两个算法程序的运行时间。其中Pecu Find在运行“100+1000”子集时，运行时间已超过1800s（0.5h），运行被中止，图3.5中用“*”表示。此图验证了前一自然段中的时间效率分析，表明CpecuFind时间效率的优势显著。
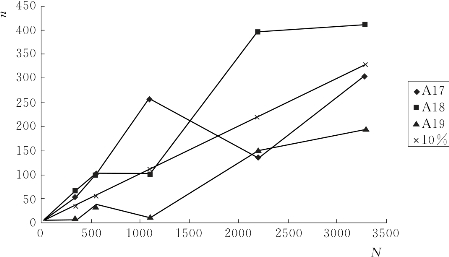
图3.4 不同数据集规模下n与N的关系图
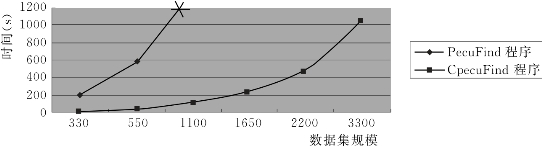
图3.5 PecuFind程序和CpecuFind程序运行时间比较
2.两算法ROC曲线对比
KDDCUP99数据集是网络访问数据记录集，其中的记录有两大类：正常访问记录和网络攻击记录，而网络攻击记录在数据集中占的比例很小，如果将攻击记录设为正类，正常访问记录设为负类，本章讨论的特异数据挖掘问题在此数据集上就是不平衡数据集的二分类问题。这类问题的结果评估，除前述的挖掘特异数据能力，还可以以ROC曲线特征来评估。对于第3.3.2节的30+300和50+500数据集，分别利用Cpecu Find和Pecu Find算法计算出的记录特异因子RPF值绘制ROC曲线，得到4个ROC曲线图，如图3.6和图3.7所示，曲线x轴表示假正率（Sensitivity），y轴表示真正率（1-Specificity）。4个ROC曲线下方面积的对比结果如表3.5所示。
表3.5 4个ROC曲线下方面积对比结果
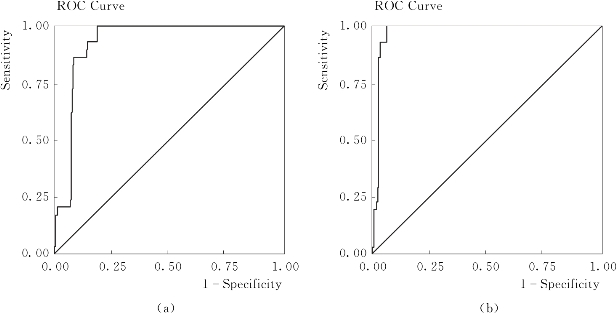
图3.6 两算法在30+330数据集上计算的ROC曲线
（a）PecuFind；（b）CpecuFind
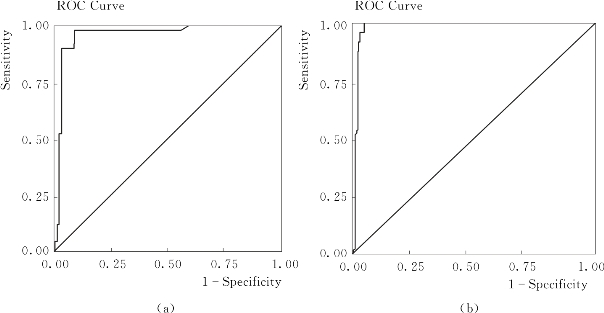
图3.7 两算法在550数据集上计算的ROC曲线
（a）Pecu Find；（b）Cpecu Find
由此，4个ROC曲线的对比说明，CpecuFind算法性能优于Pecufind算法性能。
有关数据挖掘算法及在视频分析中的应用的文章
本实验采用C++语言，使用VS2019集成开发环境。替换矩阵采用Clustal W中默认的IUB矩阵。最终比对结果与Clustal W和Clustal O的比对结果，如图5-7所示。图5-7算法结果比较通过对PAR方法和PAR平台的使用，我们运用Apla语言以半自动的方式组装形成了基于系统发生树的渐进式比对算法，并将Apla程序转换成了C++代码，得到了可运行的算法程序，算法结果与Clustal W和Clustal O进行了比较，基本的保守位点和相似区域都可有效发现，具有一定的生物学意义。......
2023-10-25
9.4.5.2调度优化性能分别以32，64，80，100个任务量的仿真场景进行计算，对于每个场景进行100次仿真优化，优化结果取均值与标准遗传算法的优化结果进行比较，比较结果如表9-5所示。......
2023-07-02
之后计算求得该组5个制品减重百分数的平均值xi，作为该组实验的结果。表6-9 实验结果表6-10 实验结果表6-11 实验结果表6-9～表6-11中，每一行为一组实验数据，各因素下为对应的水平号。表6-10～表6-11中实验号5、13、14的实验结果明显小于其他数据，后续数据处理中保留了这些数据，没有作为奇异项处理。图6-32 一个注塑周期的实验数据图所有数据统一在一个时间轴下记录，为后续数据分析提供了便利。......
2023-07-02
该法在美国适用于平原区52000km2以下、山区13000km2以下的面积和6～72小时的可能最大暴雨估算。图10.19PMP时—面—深曲线2）外包。图10.21设计的控制面积内PMP暴雨模式③概化可能最大暴雨等值线图的绘制。在分析设计地区实测暴雨等值线图的基础上，确定概化暴雨图的形状。......
2023-08-23
一般地，对多目标优化算法性能的度量包括对算法所获得的近似Pareto解集的质量和为产生这样的近似解集所需计算资源的度量。直至1999年至2000年间，Veldhuizen和Lamont[1-3]提出了多目标进化算法性能度量的方法，才开启了量化评估算法性能之路。性能度量曲线应随着代数的增加呈递增或递减之势，这样更有利于不同集合之间的比较。性能度量函数的计算复杂度不能太高。......
2023-11-26
计算这些序列的频率和时间平均方差形成特征向量，利用此特征向量数据进行了多方面的实验，验证其在人的行为识别方面的有效性。实验表明，当分段长度达到30帧以上时，就可获得很高的分类精度，且分段长度的变化对识别精度影响就会很小了。......
2023-06-16
在COPA方法的基础上，Tibshirani等人在2007年提出的OS方法引入了分位数做启发式规则附加表达值，进行差异表达基因检测。由于差异估算中用正常组样本中值代替了全部数据的中值，ORT方法比COPA方法和OS方法恰当地估计了两组数据的差异。COPA方法和OS方法随差异数目的增加，性能有所降低。Lian在2008年提出的MOST方法隐性地考虑了差异基因表达强度临界值所有可能的取值，通过确定其统计量最大值来确定阈值，从而检测差异表达基因。......
2023-11-21
鉴于此，我们从一般意义上分析MSMOPSO的收敛性。MSMOPSO算法在粒子的速度更新中增加了扰动项，并且设置了随机量r3在[-1，1]区间内均匀取值，增加了粒子飞行方向的多样性，另外，MSMOPSO算法在步骤4对粒子群中所有的粒子以一定的概率执行多项式变异，这些变异的措施能够保证粒子群搜索的范围覆盖至整个决策空间。综合上述定性分析可知，MSMOPSO算法能够收敛至问题的全局最优前沿。......
2023-11-26
相关推荐