基于聚类的全局特异数据挖掘算法

2025-09-29 理论教育版权反馈

【摘要】：设某一属性的所有值的数据集为S，其平均值为Smean。根据这些想法，提出一种基于聚类的全局特异数据挖掘方法。构架仍由挖掘特异属性和挖掘特异记录两个层次构成。从原则上讲可以采用任何基于距离的聚类算法对S进行聚类，采用的聚类算法的效果好，可以减少后续的计算量。图3.2SimC聚类算法可以看出，k是控制聚类半径Cd的。现在根据式（3.9）计算每个类的特异因子，记为CPF。显然，CPF越小的类，其中的元素是特异数据的可能性越小。

特异数据在整个数据集中占的比例很小，第3.1节的构架中有大量的冗余运算。设某一属性的所有值的数据集为S，其平均值为Smean。如果事先根据距离将S进行聚类，那么大类（其中数据个数多的类）中的数值成为特异的可能性就会很小，质心（类中数据的平均值）距Smean较近的类中的数值成为特异的可能性也会很小。第3.1节的构架精确地计算出了所有属性与记录的特异因子，而用户关心的只是特异值排序在前面的很少一部分属性与记录的特异因子值，对于排序在后面的特异因子值可以采用不精确的计算方法。根据这些想法，提出一种基于聚类的全局特异数据挖掘方法。

给定一个数据集D，D是由属性和记录组成的二维关系表。数据集的结构如表3.1所示。首先，一个百分数λ需要由用户给出。λ表示数据集D中特异数据占的比例，可以是用户预测D中有≤λ×|D|个特异数据或用户希望能找出前λ×|D|个特异值。另外，还需要设置一个聚类系数k，其值为2或3或4，可由用户指定，默认k=2。k的意义将在后面说明。构架仍由挖掘特异属性和挖掘特异记录两个层次构成。

在属性层次，首先，将每个属性按距离进行聚类；之后，计算每个属性聚类的反特异因子，并将属性聚类分成可能成为特异的类和不可能成为特异的类；最后，计算属性的特异因子并排序，指定前λ×|D|属性为特异的。

设某一属性的所有值的集合为S，其平均值为Smean。从原则上讲可以采用任何基于距离的聚类算法对S进行聚类，采用的聚类算法的效果好，可以减少后续的计算量。为了时间效率，使用的是一种类似于Squeezer算法[111]和文献[112]中聚类算法的简单聚类算法，称SimC（Simple Cluster），如图3.2所示。SimC算法思想简单，运行效率高。虽然聚类的结果并不优秀，但后面的实验将证明，SimC有效地支持了本章的构架。

pagenumber_ebook=41,pagenumber_book=36

图3.2　SimC聚类算法

可以看出，k是控制聚类半径Cd的。k越大，Cd越小，产生的类越多，同时每个类更精细。设S经聚类生成{C1，C2，…，Cη}η个类。现在根据式（3.9）计算每个类的特异因子，记为CPF（Cj）。式中，|Cj|表示类Cj中元素的个数。

pagenumber_ebook=42,pagenumber_book=37

显然，CPF越小的类，其中的元素是特异数据的可能性越小。将η个类按CPF由大到小的顺序排序，设排序后的顺序为：C1′，C2′，…，Cη′。再设置一个阈值，称红蓝界RBB，并且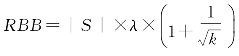 pagenumber_ebook=42,pagenumber_book=37 ，k是之前设定的聚类系数。从C1′开始累计类中元素个数，设当累计到Cjr′时结果第1次大于或等于RBB，则称C1′，C2′，…，Cjr′为红类；Cjr+1′，Cjr+2′，…，Cη′为蓝类。

计算每个属性的特异因子PF时，红类中的元素将作为单个的值参加运算，也会有自己的PF值，蓝类将整个类参加运算，类中的元素共用一个PF值。设经聚类和分类后，类的序列为：C1′，C2′，…，Cjr′，Cjr+1′，Cjr+2′，…，Cη′，且红类为前jr个，所有红类中元素总个数的和为nr，属性PF值新的计算方法如式（3.10）～式（3.12）。

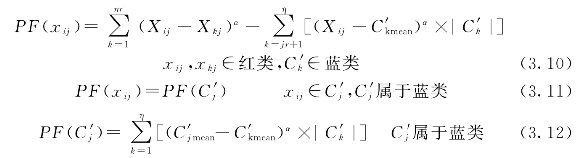pagenumber_ebook=42,pagenumber_book=37 (https://www.chuimin.cn)

由式（3.10）～式（3.12）可以计算出表3.1中全部属性的PF值。计算记录的RPF时，对式（3.3）稍作变动，变为式（3.13），从先横向再纵向变到先纵向再横向。因为有大批属蓝类的属性有相同的PF值，式（3.3）的计算就可大大简化。

pagenumber_ebook=42,pagenumber_book=37

从聚类开始，经过前面的计算，可以得到每个属性的PF值和每个记录的RPF值。与第3.1节的构架不同的是，这里不需要p和pr来判断属性和记录的特异性，因为用户指定了λ，所以将PF从大到小排序，RPF从大到小排序，分别指定前λ×|D|个为特异的即可。

对于二维关系表的属性a1，a2，…，am的处理，与第3.1节类似。如果aj是表的主键，它是用来标识记录的，不需要计算其PF值；如果aj是表的外键，那么它是另一个表的主键，其PF值由那张表的RPF来确定；只有aj是表的一般属性时，才有必要计算其PF值。

对于不能区分等级的文本属性值，在聚类时可以简单地将具有相同值的聚为一类；计算类的CPF时，使用公式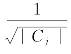 pagenumber_ebook=43,pagenumber_book=38 ；计算两个值的距离时，按相同为0，不同为1的原则进行；计算属性PF时，只使用式（3.12）按类计算，其余的计算均可照常进行。

在使用式（3.13）计算整个记录的RPF（Xi）时，用户可以调节βj来控制各属性的权。为避免属性自身值的不平衡而给RPF造成的影响，计算RPF前应对属性的PF进行标准化（当然也可以采用将属性标准化的方法）。因为计算PF的标准差σ的时间复杂度是O（n2），可以采用式（3.14）来进行PF的标准化。其中，PFjmax和PFjmin分别是属性aj的PF值中的最大值和最小值。

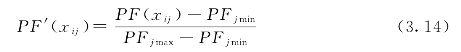
pagenumber_ebook=43,pagenumber_book=38

根据新的构架，将特异计算过程总结为算法，称为CpecuFind算法，如图3.3所示。

pagenumber_ebook=43,pagenumber_book=38

图3.3　CpecuFind算法

基于聚类的全局特异数据挖掘算法

相关推荐