多分类器融合及性能评估分类算法

2025-09-29 理论教育版权反馈

【摘要】：多分类器融合就是融合多个分类器提供的信息，得到更加精确的分类结果。多数据投票法和BKS方法均是决策层的多分类器融合方法。利用训练集数据学习获得一个分类器，然后使用测试数据集对该分类器分类精度进行评估。

1.多分类器融合

过去10多年中，对分类器研究的焦点从单个分类器的研究转移到多分类系统的研究。多分类器融合就是融合多个分类器提供的信息，得到更加精确的分类结果。融合多分类器的特长是系统研究的目标，其必要性体现在两个方面[91]：

（1）分类方法有很多，这些方法是基于不同的理论框架提出来的。每种分类器各有优点，对于特定的应用问题，都能够取得一定的成功。但是，没有一种方法适应所有的应用需求。从大量的实验和应用中发现，不同的分类器对于分类模式具有互补的信息，可以利用互补信息来提高识别性能。

（2）对于复杂的识别问题，输入的特征变量较多。变量类型、表现形式不同。对于不同表现形式和不同物理含义的特征变量，进行归一化处理非常困难，难以用一个分类器来处理。另外，当输入特征向量较大时，分类器的结构将变得非常复杂，限于样本的规模，学习的程度也不同。利用信息融合的思想，可能设计一个性能优良的高维输入分类器问题转化成多个性能较优的低维输入分类器的设计问题，为高维特征空间的划分和高可行性分类器的设计提供一个新的思路。

根据各分类器提供的信息的级别，多分类器的融合可分为以下3种类型[91]：

（1）决策层融合，即单个分类器输出为某个确定的类标号。假设R个分类器e1，e2，…，eR对同一输入标本x进行分类，事件ek（x）=jk表示分类器ek把x划分到Wjk中，其中，jk∈Λ∪{M+1}，{M+1}表示分类器ek拒识x，k=1，2，…，R。决策层融合就是利用这些事件构造一个集成的分类器e对x进行分类，输出一个确定的类别号，e（x）=j，j∈Λ∪{M+1}。多数据投票法和BKS方法均是决策层的多分类器融合方法。

（2）排序层融合，即单个分类器输出为样本属于各类的可能性的一个排序列表。对于输入x，每个分类器ek（x）产生一个子集Lk⊆Λ，且Lk中标签排列成一个序列。排序层融合就是利用事件ek（x）=Lk，k=1，2，…，R，构造一个集成的分类器e，对x进行分类，输出一个确定的类别号，e（x）=j，j∈Λ∪{M+1}。

（3）度量层融合，即单个分类器输出为样本属于相应类的程度。对于输入x，每个分类ek（x）器产生一个度量向量Me（k）=[mk（1），mk（2），…，mk（M）]T，其中，mk（i）表示s属于相应类wi的程度。度量层融合就是利用事件ek（x）=Me（k），k=1，2，…，R，构造一个集成的分类器e，对x进行分类，输出一个确定的类别号，e（x）=j，j∈Λ∪{M+1}。

3类方法利用的分类器输出信息量集资增多，相应地也可能得到更好的结果。

2.分类算法性能评估

分类精度是度量分类效果的最主要指标，一般定义为被分类器正确分类的对象数与被分类的所有对象数之比。为测量分类精度，一般将数据集随机划分为两个部分：一个作为训练数据集；另一个则作为测试数据。通常训练集包含初始数据集的2/3的数据，而其余的1/3则作为测试数据集的内容。利用训练集数据学习获得一个分类器，然后使用测试数据集对该分类器分类精度进行评估。这种评估过程一般被称为holdout[97]。holdout评估分类器过程示意如图2.13所示（来源于文献[97]中图4.16）。由于仅使用初始数据集中的一部分进行学习，因此对所得分类器预测精度的估计应是悲观的估计。随机取样是holdout方法的一种变化。在随机取样方法中，重复利用holdout方法进行精度评估k次，最后对这k次所获得的精度求平均，来获得最终的精度值。

pagenumber_ebook=30,pagenumber_book=25

图2.13　用holdout方法评估分类器精度的过程

k-交叉检验（k-cross validation）是随机二次抽样方法的交叉验证。初始数据集被随机分为k个互不相交的子集S1，S2，…，Sk，每个子集大小基本相同。学习和测试过程分别进行k次，每一次选择一个子集作为测试集，其他子集则合并到一起构成一个大训练数据集，通过学习获得分类器，对测试集进行测试，获得精度。一般第1次选择S1作为测试集，第2次选择S2作为测试集……最终的精度可用k次测试的平均精度来表征。

除精度外，评估分类算法性能的还包括其速度、鲁棒性、可规模性和可解释性等。鲁棒性一般评估分类器对噪声的敏感程度；可规模性可以通过计算给定分类算法在渐增的数据集上的I/O操作次数评估；可解释性是主观的度量。

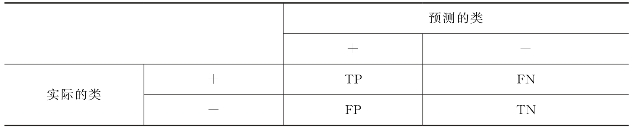
对于不平衡数据集的二分类问题，数据集中只有大类和小类两类，由于两类数据比例不均衡，精度值一般不能准确表征分类的效果。例如，对于网络访问数据集，其记录一般90%以上是大类数据，是正常访问的数据，小于10%的记录是入侵访问。如果简单地将所有记录判定成正常记录，其正常记录的分类精度也会大于90%，而这个值是无意义的。在这类数据集中，二类记录不是同等重要的，受关注的是小类记录，一般称为正类样本，而大类记录称为负类样本。为此，一些新的度量指标是必需的[97]。为说明这些指标，需声明4个数值术语的定义：真正、假负、假正、真负[97]。混淆矩阵是用来表示这4个术语的汇总表格，其示意如表2.2所示（源于文献[97]中的表5.6）。

1）真正（true positive，TP）对应于被分类模型正确预测的正样本数。

2）假负（false negative，FN）对应于被分类模型错误预测为负类的正样本数。

3）假正（false positive，FP）对应于被分类模型错误预测为正类的负样本数。

4）真负（true negative，TN）对应于被分类模型正确预测的负样本数。

表2.2　类不同等重要的二分类问题混淆矩阵

pagenumber_ebook=31,pagenumber_book=26

真正率（true positive rate，TPR），也称灵敏度（sensitivity），或称召回率（recall），被定义为模型正确预测的正样本的比例，即：

pagenumber_ebook=31,pagenumber_book=26

真负率（true negative rate，TNR），也称特指度（specificity），定义为被分类器正确预测的负样本的比例，即：(https://www.chuimin.cn)

假正率（false positive rate，FPR），定义为被分类器预测为正类的负样本比例，即：

假负率（false negative rate，FNR），定义为被分类器预测为负类的正样本比例，即：

pagenumber_ebook=32,pagenumber_book=27

那么，前述的精度即被正确分类的正样本数与被正确分类的负样本数之和占全部样本数的比例，表达为：

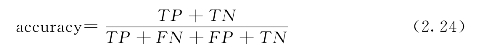
pagenumber_ebook=32,pagenumber_book=27

可以构造一个基线模型，它最大化其中一个度量而不管另一个。例如，将每个记录都声明为正类，则召回率永远是1，但它的精度等值会很差。构建一个最大化精度和召回率的模型是分类算法的一个主要挑战。

另外，一个可以调和精度和召回率的指标F 1被定义为：

接受者操作特征曲线（receiver operating characteristic curve，ROC）是显示分类器真正率和假正率之间折中的一种图形化方法[97]。在ROC图中，一般x轴表示假正率（在SPSS分析结果图中用1-sepecificity标记），y轴表示真正率（也称灵敏度，在SPSS的分析结果图中用sensitivity标记），其示意如图2.14所示[来源于本书第3.4节的图3.6（a）]。

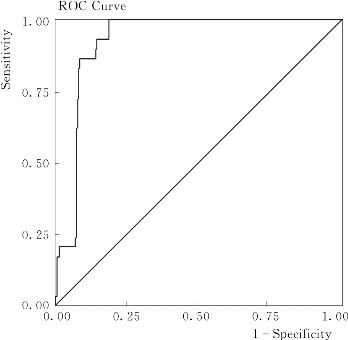
pagenumber_ebook=32,pagenumber_book=27