BP算法结束了多层网络没有训练算法的历史，并被认为是多级网络系统的训练方法，它有很强的数学基础，故其连接权的修改是令人信服的。因为已有结果表明一层隐含层已经足够近似任何连续函数，故图像目标识别系统常常采用三层BP神经网络。......
2023-06-28
神经网络分类：方法优化
【摘要】：1943年，心理学家Mcculloch和数学家Pitts合作提出形式神经元的数学模型，成为人工神经网络研究的开端。神经网络的原始模型是1958年提出的感知器模型，只有一个输出节点，它相当于单个神经元，主要用于模式分类。几乎所有神经网络学习算法都可以看做Hebb学习规则的变形。图2.12多层前馈网络结构示意图多层前馈网络的适用范围大大超过原始网络，但其主要困难是中间的隐层不直接与外界连接，无法直接计算其误差。为解决这一问题，提出了反向传播算法。
1943年，心理学家Mcculloch和数学家Pitts合作提出形式神经元的数学模型，成为人工神经网络研究的开端。1949年，心理学家Hebb提出神经元之间突触联系强度可变的假设，并据此提出神经元的学习准则，为神经网络的学习算法奠定了基础。1982年，Hopfield提出了神经网络的一种数学模型，引入了能量函数的概念，研究了网络的动力学性质，又设计出用电子线路实现这一网络的方案，同时开拓了神经网络用于联想记忆和优化计算的新途径，大大促进了神经网络的研究。
神经网络的原始模型是1958年提出的感知器模型，只有一个输出节点，它相当于单个神经元，主要用于模式分类。感知器的功能是有限的，它无法解决线性不可分的两类样本的分类问题。之后，人们又提出了多层前馈网络及反向传播训练算法，简称BP网络或BP算法。
多层前馈网络结构如图2.12所示（来源于文献[93]中图11.3）。构成前馈网络的各神经元接受前一级输入，并输出到下一级、无反馈，形成一有向无环图。除输入和输出层，中间的层称为隐层。图的节点分为两类，即输入节点与计算单元。几乎所有神经网络学习算法都可以看做Hebb学习规则的变形。Hebb学习规则的基本思想是：如果神经元Ui接收来自另一神经元Uj的输出，则当这两个神经元同时兴奋时，则从Uj到Ui的权就得到加强。
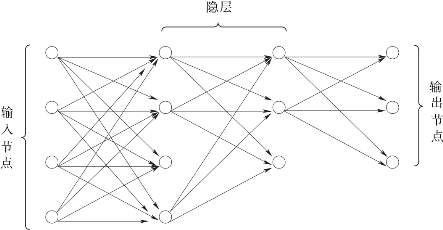
图2.12 多层前馈网络结构示意图
多层前馈网络的适用范围大大超过原始网络，但其主要困难是中间的隐层不直接与外界连接，无法直接计算其误差。为解决这一问题，提出了反向传播算法。其主要思想是从后向前（反向）逐层传播输出层的误差，以间接算出隐层误差。算法分为两个阶段：第一阶段（正向过程）输入信息从输入层经隐层逐层计算各单元的输出值；第二阶段（反向传播过程）输出误差逐层向前算出隐层各单元的误差，并用此误差修正前层权值。反向传播算法解决了隐层权值修正问题，但它是用梯度法求非线性函数极值，因而有可能陷入局部极小点，不能保证收敛到全局极小点[93]。
利用神经网络进行分类时，如果训练样本是M维模式向量，它们依次送到神经网络的输入层，用来训练神经网络的参数。输入层各节点以一定权值送到第一隐层各节点，第一隐层各节点输出再以一定权值送到第二隐层各节点。最后，第二隐层节点分别送到输出层，得到运算结果。
观察第一隐层诸神经元，它们有共同的输入和不同的输出。每个这样的神经元都是感知器，它决定了多维空间的不同超平面。每个超平面将M维空间分割成正负两个半空间。给出的超平面通过以后的连接和组合构成一个正确的分段线性划分，这个分段线性划分能拟合对这些类模式正确分类的超曲面。这就把模式识别中的分段线性划分与前馈神经网络联系了起来[96]。
有关数据挖掘算法及在视频分析中的应用的文章
- 详细阅读
-
淬火工件分类方法优化详细阅读
淬火工件分类便于选择材料、制订热处理的工艺方法，考核热处理技术经济指标。以工件的尺寸分类 有效尺寸不大于100mm的零件为薄件，大于100mm的零件为厚件。中淬透性钢件 这类钢的热处理淬火临界尺寸在60mm以下，常选用油冷淬火，对于大于这个尺寸的工件需要采用水—油双液淬火来达到技术要求。......
2023-06-24
-
基于规则的分类方法优化策略详细阅读
仔细研究各算法就会发现，决策树分类算法、关联规则分类算法、贝叶斯分类算法都是基于规则“A→C”和其统计特性的。C 4.5是决策树分类算法的代表[98]。构造决策树时，总选择增益比例大的属性作为下一分支节点。简化后的规则按类进行分组，形成最终的分类规则集。可见，贝叶斯分类器也是基于规则“A→C”的统计特性的。决策树分类法是一种直观且精度较高的方法，但决策树有时也会变得很复杂，以至于难以解释。......
2023-06-16
-
数据分区与分类的优化方法详细阅读
图7-41 FANUC系统的存储空间和储能电容2.数据的分类机床数据文件主要分为系统文件、机床厂文件和用户文件三种。其中，系统文件为FANUC公司提供的CNC控制软件和伺服控制软件等；MTB文件包括PMC程序等；用户文件包括CNC参数、PMC参数、螺距误差补偿值、用户宏程序变量、刀具补偿值、加工程序、对话式编程数据、操作履历数据及伺服波形诊断数据等。表7-6 FANUC系统FROM中的文件注：□表示1个字符的数字，表示1个字符的字母或数字。......
2023-06-23
-
电接触材料分类优化：了解电接触材料的分类方法详细阅读
作为高、低压开关电器的关键部件，电接触材料是制约触头性能的主要因素。电接触材料性能的优劣直接决定整个电器或系统的使用寿命及运行可靠性。表3-6常用电接触材料分类过去，Ag-CdO系电接触材料在低压电接触材料中占据主导地位。Ag-CdO系电接触材料之所以具有如此良好的性能，与CdO（氧化镉）的下述作用分不开。近年来，随着纳米技术的发展，新型纳米Ag-SnO2电接触材料的研究与应用是其今后发展的一个方向。......
2023-06-30
-
支持向量机分类方法优化为：掌握支持向量机的分详细阅读
由线性判别函数的设计过程可知，对于线性可分集，总能找到使模式样本正确划分的解。d维空间中线性判别函数的一般形式为g=ωX+b，分类面方程为：ωX+b=0将判别函数进行归一化，使两类所有样本都满足|g|＞1，这样分类间隔就等于2/‖ω‖。对于线性不可分问题，可以用类似于广义线性判别函数的方法，通过事先选择好的非线性映射将输入模式向量映射到一个高维空间，在这个空间中构造最优分界超平面。......
2023-06-16
-
特殊儿童分类的优化原则详细阅读
特殊儿童的分类首先牵涉分类的伦理问题，有赞成分类的，有反对分类的。因此，特殊儿童的分类犹如一把双刃剑，积极性与消极性相伴而生。因此，对于特殊儿童的分类，一般认为必须秉持两个基本原则：无歧视原则和去标签化原则。这是消除分类造成消极标签化影响的首要原则。这样才能明晰和把握特殊儿童的身心特点，实施有针对性的教育。但是，在对特殊需要儿童进行教育时，应确立一种无歧视的教育理念，以科学有效的方法进行分类。......
2023-07-02
-
神经网络方法在桥梁可靠度分析中的应用详细阅读
人工神经网络在最近几十年里无论是在理论或是在应用上的研究都取得了很大的进展。此外，神经网络具备良好的泛化能力，相比传统的多项式响应面方法精度和效率更高。常规神经网络的结构如图3.1所示。图3.1神经网络示意图人工神经网络主要有以下几种较为常见的类型：反向传播-BP神经网络。BP网络是一种遵循误差逆向传播算法训练得到的多层前馈式网络，也是当前应用较广泛的ANN之一。......
2023-09-19
相关推荐