支持向量机是Vapnik及其合作者［130］根据结构风险最小化原则提出的一种在高维特征空间使用线性函数假设空间的学习系统。支持向量机是机器学习领域若干标准技术的集大成者。在若干挑战性的应用中，获得了目前为止最好的性能。，xn)′标记为正类，否则，将其标记为负类。图3-4 二维训练集的分开超平面(w,b)图3-5 最优超平面对于多个模式类的分类问题，输出域是Y={1，2，…......
2023-06-28
支持向量机分类方法优化为：掌握支持向量机的分类技巧
【摘要】：由线性判别函数的设计过程可知，对于线性可分集，总能找到使模式样本正确划分的解。d维空间中线性判别函数的一般形式为g=ωX+b，分类面方程为：ωX+b=0将判别函数进行归一化，使两类所有样本都满足|g|＞1，这样分类间隔就等于2/‖ω‖。对于线性不可分问题，可以用类似于广义线性判别函数的方法，通过事先选择好的非线性映射将输入模式向量映射到一个高维空间，在这个空间中构造最优分界超平面。
由线性判别函数的设计过程可知，对于线性可分集，总能找到使模式样本正确划分的解。一般说来，它有无穷多个解，希望找到一个最优的解。一种最优的分界准则是使两类模式向量分开的间隔最大。如图2.11所示是两类线性可分集被超平面隔开的情况（来源于文献[96]中图2.14）。图2.11（b）比图2.11（a）中两类样本分开的间隔要大，如果图2.11（b）中的H0是具有最大间隔的解平面，则称这个解平面是最优的，其中距离最优分界面最近的位于间隔边界上的那些模式向量就叫做支持向量。
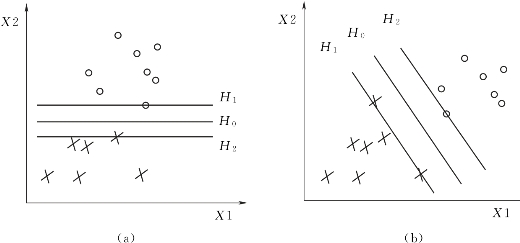
图2.11 两类线性可分集最优划分示意图
设线性可分两类样本集为（Xi，Yi），i=1，…，n，X为特征属性，Y值为+1或-1，表示两个类别。d维空间中线性判别函数的一般形式为g（x）=ωX+b，分类面方程为：
ωX+b=0 (2.19)
将判别函数进行归一化，使两类所有样本都满足|g（x）|＞1，这样分类间隔就等于2/‖ω‖。满足分类条件且‖ω‖最小的分类面就是最优分类面，最终转化为求极值解问题。
对于线性不可分问题，可以用类似于广义线性判别函数的方法，通过事先选择好的非线性映射将输入模式向量映射到一个高维空间，在这个空间中构造最优分界超平面。
有关数据挖掘算法及在视频分析中的应用的文章
- 详细阅读
-
支持向量机优化算法详细阅读
支持向量机是机器学习中的一项新技术，是借助于最优化方法来解决机器学习问题的新工具，开始成为克服维数灾难和过学习等困难的强有力的手段。支持向量机方法建立在统计学理论的VC维理论和结构风险最小原理基础之上，根据有限样本在模型的复杂性和学习能力之间寻求最佳折中，以期获得最好的推广能力。支持向量机正是这样一种努力最小化结构风险的算法。这个归一化的结果便是支持向量机的几何间隔。......
2023-06-28
-
桥梁可靠度分析方法应用：支持向量回归详细阅读
支持向量机是由Vapnik［7］提出的一种机器学习方法，主要有支持向量分类和支持向量回归两种算法。由于SVR是目前结构可靠度分析中的一种较为新颖的方法，下文将简单介绍SVR在结构响应函数拟合应用中的相关理论。SVR学习理论主要是通过如式（3.2）所示的ε敏感函数［8］来控制SVR模型的拟合误差。由式（3.5）可得到SVR模型的函数表达式：为了提高建立SVR模型的效率与精度，可通过对输入样本点及SVR模型参数进行优化。......
2023-09-19
-
凿岩机的分类和安全操作技巧详细阅读
此外，凿岩机也可改作破坏器，用来破碎混凝土之类的坚硬层。凿岩机按其动力来源可分为内燃凿岩机、风动燃凿岩机、电动凿岩机和液压凿岩机等四类。这些凿岩机的冲击机构在回程时，由转钎机构强迫钢钎转动角度，使钎头改变位置继续凿击岩石。......
2023-06-29
-
传真机的演变及分类方法详细阅读
1843年美国物理学家亚历山大·贝思发明传真机。传真机的发展经历了基础探索、发展普及和多功能化3个主要阶段。传真机真正进入大众化阶段是在文件传真三类机出现之后短短几十年的时间。目前，以G4为代表的传真机正朝着高速化、网络化、综合化、一体化、智能化、小型化的方向发展。传真机种类繁多，其分类方法也多种多样。按照信号的形式可以把传真机分为模拟和数字两种。按色调分，黑白传真机、彩色传真机及相片传真机。......
2023-06-18
-
如何分类刻录机？详细阅读
刻录机可以分两种，一种是CD刻录，另一种是DVD刻录。现在市场上还有一种CD-RW的刻录机和盘片，这种CD-RW是可以擦写的，而巨擦写次数可高达一千次以上。以4X的DVD-RW刻录机为例，刻满一张4.7GB的DVD-R光盘耗时还不到15min。......
2023-06-22
-
热力机：原理、分类及比较详细阅读
汽车用发动机是热力机的一种。热力机的运行原理根据其热效果的不同而有所差异。热力机就是通过热能的传递使流体发生膨胀和收缩，把热能转换成机械能的装置。外燃机的燃烧气体与工质流体不是同一种气体，且产生热量的部分和发生动力的部分各自独立。根据工质流体转换为功的方式不同，热力机可分为往复型和旋转型。表1-1 热力机的分类和比较......
2023-06-28
-
汽车用内燃机的分类详解详细阅读
根据不同的分类方法，汽车用内燃机可分为多种类型。②压燃式发动机：在进气行程气缸内仅空气进入并压缩达到燃料自发着火温度以上后，向气缸中以高压喷射雾状燃料，并自发着火燃烧的类型，可以做成大输出功率的大型发动机。......
2023-06-28
相关推荐