设某一属性的所有值的数据集为S，其平均值为Smean。根据这些想法，提出一种基于聚类的全局特异数据挖掘方法。构架仍由挖掘特异属性和挖掘特异记录两个层次构成。从原则上讲可以采用任何基于距离的聚类算法对S进行聚类，采用的聚类算法的效果好，可以减少后续的计算量。图3.2SimC聚类算法可以看出，k是控制聚类半径Cd的。现在根据式（3.9）计算每个类的特异因子，记为CPF。显然，CPF越小的类，其中的元素是特异数据的可能性越小。......
2023-06-16
聚类的方法：优化数据分析过程
【摘要】：聚类的定义与待处理对象特征有关。聚类的方法很多，不同的方法对于同一数据集聚类的结果可能不同。根据层次分解形式的方式，层次聚类方法可划分为凝聚的层次聚类和分裂的层次聚类方法。绝大多数层次聚类方法属于这一类，它们的不同表现在簇内与簇间相似度的定义不同。目前，一般将基于层次的聚类方法和其他聚类技术进行集成以形成多阶段聚类，从而提高聚类质量。它是一种结构辅助聚类的方法，在大型数据库中的速度和伸缩性较好。
聚类分析的思想就是根据“物以类聚”的原理，将样本或模式进行分类。聚类的定义与待处理对象特征有关。基于不同的模型构造思想，提出了一系列更加具体化的定义[95]：
（1）基于距离的定义。一个聚类是这样一组数据的集合，其聚类成员之间距离的最大值小于这些成员到任一非聚类成员距离的最小值。显然，这种定义方法过于机械，它对于刻画复杂数据聚类的能力较弱。
（2）基于质心的定义。在数据集合中指定若干个质心，根据各数据点到这些质心的距离划分聚类，它使得一个聚类中的元素到其质心的距离小于其到任何其他质心的距离。这种定义方法一般只能够恰当地描述球形聚类，它不适于描述不规则形状的聚类。
（3）基于连接的定义。一个聚类是一组彼此连接的数据点的集合，每个数据到聚类中其他数据之间的接近程度大于其到非聚类成员之间的接近程度。这种定义方法的有效性在于它能够描述任意形状的聚类，但当数据集包含噪声时，基于连接的定义方法难以区分夹杂于噪声数据之间的不同聚类。
（4）基于密度的定义。聚类是数据空间中的稠密区域元素所构成的子集合，两个聚类之间的边界通过稀疏区域划定。基于密度的定义能够适应聚类形状不规则和包含噪声数据的情形，因此它较之其他定义方法具有独到的优越性。
（5）基于相似性的定义。聚类是一组“相似”数据对象的集合，处于不同聚类的元素彼此互不“相似”。
聚类的方法很多，不同的方法对于同一数据集聚类的结果可能不同。以下介绍划分法和层次方法[95]。
1.划分法
给定包含n个数据对象的数据集，并给定所要形成的聚类个数K（K＜n），划分算法将对象集合划分为K份，其中每个划分均代表一个聚类，所形成的聚类将使得同类中的对象是“相似”的，而不同聚类中的对象是“不相似”的。
K-均值（K-means）聚类方法是最典型的划分方法，将n个对象划分成K个聚类，确保聚类内具有较高的相似度，而聚类间的相似度较低。其处理流程为：首先从n个数据对象中随机选择K个数据对象作为初始聚类的中心，而对于余下的每个对象，根据其与各个聚类中心的距离或相似度，分别将它们分配给与其最相似的聚类；然后重新计算每个聚类的平均值。这个过程不断重复，直到目标测度函数开始收敛。其目标测度函数通常采用平方误差准则，即：
式中：E为所有聚类对象的平方误差和；p为聚类对象；mi为类Ci的各聚类对象的平均值。
K-均值算法具体描述如图2.9所示。
当结果簇是密集的，而簇与簇之间区别明显时，K-means算法效果较好。对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度是O（nkt），n是所有对象的数目，k是簇的数目，t是迭代的次数。通常情况下，k≪n，且t≪n。
图2.9 K-均值算法
但是，K-means算法只有在簇的平均值被定义的情况下才能使用，且用户指定的k值在很多应用中依据不容易把握。另外，K-means算法不适合于发现非凸形状的簇，或者大小判别很大的簇。而且，它对于噪声和孤立点敏感，少量的该类数据能够对所属簇的平均值产生极大的影响[25]。
K-means算法有很多变种。它们可能在初始k个平均值的选择，相异度的计算，计算聚类平均值的策略上有所不同。经常会产生较好的聚类结果的一个策略是，首先采用层次的自底向上算法决定的结果簇的数目及找到初始的簇，然后用迭代的重定位来改进聚类结果[25]。
K-means算法的一个变体是k-modes方法，它扩展了K-means算法，用模式来替代类的平均值，采用新的相异性度量方法来处理分类性质的数据，采用基于频率的方法来修改聚类的模式。K-means算法和k-modes方法可以综合起来处理有数值类型和分类类型属性的数据，这就是k-prototypes方法[25]。
期望最大（Expectation Maximization，EM）算法以另一种方式对Kmeans算法进行了扩展。它不把对象分配给一个确定的簇，而是根据对象与簇之间隶属关系发生的概率来分派对象。换句话说，在簇之间没有严格的界限[25]。
2.层次方法
层次方法就是通过分解所给定的数据对象集来创建一个层次。根据层次分解形式的方式，层次聚类方法可划分为凝聚的层次聚类和分裂的层次聚类方法。
（1）凝聚的层次聚类是自底向上的策略。首先将每个对象作为一个簇，然后合并这些原子簇为越来越大簇，直到所有的对象都在一个簇中，或者某个终结条件被满足。绝大多数层次聚类方法属于这一类，它们的不同表现在簇内与簇间相似度的定义不同。
（2）分裂的层次聚类是自顶向下的策略。首先将所有对象归为一个簇中，然后逐渐细分为越来越小的簇，直到每个对象自成一簇，或者达到了某个终结条件，例如达到了某个希望的簇数目，或者两个最近的簇之间的距离超过了某个阈值。
在凝聚或分裂的层次聚类方法过程中，簇间距离是重要的依据，目前广泛采用的簇间距离的度量方法一般有4种[25]：
1）最小距离：
2）最大距离：
3）平均值距离：
4）平均距离：
这里，|p-p1|是两个对象p和p1之间的距离；Ci是簇的平均值。
由于划分的不可逆性，这种方法的最大困难在于聚类过程中对聚类进行合并或分裂的选择，不适宜地选择合并或分裂会导致低质量的聚类结果。此外，每次决定聚类的合并还是分裂都需要检验和计算大量的数据对象和聚类，因此效率较低[95]。目前，一般将基于层次的聚类方法和其他聚类技术进行集成以形成多阶段聚类，从而提高聚类质量。常用的层次方法有最短距离法、最长距离法、中间距离法、BIRCH、CURE和Chameleon等[95]。
BIRCH（Balanced Iterative Reducing and Clustering Using Hierarchies）是利用层次方法的平衡迭代约减和聚类方法[25]。它引入了两个概念：聚类特征和聚类特征树（CF tree），用于概括聚类过程的描述。它是一种结构辅助聚类的方法，在大型数据库中的速度和伸缩性较好。
一个聚类特征（CF）是一个三元组，用来描述子类（cluster）对象的信息。假设某个子类中有n个d维的对象或点{oi}，则式（2.11）、式（2.12）、式（2.13）定义了该子类的质心x0、半径R和直径D。
R和D反映了整个子类围绕它的质心的紧密程度。
而该子类的CF定义如式（2.14）。
CF=(n,LS,SS) (2.14)
式中：n为子类中点的数目；LS为n个点的和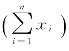
；SS为n个点的平方和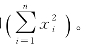
CF有效地记录了子类的要素，而不是存储所有子类中的对象。
CF树是高度平衡的树，它存储了层次聚类的特征。如图2.10所示是一个CF树的示意图（原图来源于文献[25]中图7.8）。树中的非叶节点有后代或子树，非叶节点存储了其后代的CF的和，也就是概括了其子节点的聚类信息。一棵CF树有两个参数：分支因子B和阈值T。分支因子定义了树中非叶子节点的最大子节点数目，阈值T给出了树中叶子节点的最大直径。两参数会影响生成树的大小。
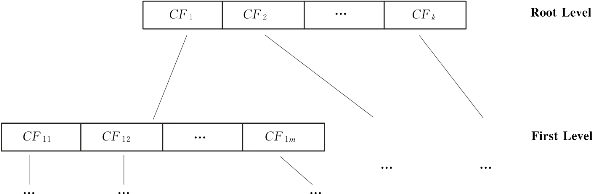
图2.10 CF树结构示意图
BIRCH算法包括两个阶段[25]：
（1）扫描数据集，建立一个初始CF树，CF树一般存放在内存中。这个CF树压缩了数据集信息，只保留了聚类所需的数据信息。
（2）采用某个聚类算法对CF树的节点进行聚类。
在阶段（1），随着新的数据对象被处理，CF树被动态构造，这个方法对增量聚类有很好的支持。一个数据对象被插入到最近的叶子。如果在插入后存储在叶子节点中的子类的直径大于阈值T，那么该叶子就会被分裂。新的数据对象插入后，其信息向树根传递。如果CF树构造过大，不适应内存，可以定义一个较小的阈值，并重建CF树。重建过程从旧树的叶子节点构造新树，不需重读数据集。因此，为了构建CF树，一般只需读一个数据集。
在阶段（2），利用构建的CF树来生成最好的聚类。BIRCH采用了一种多阶段聚类技术，一遍扫描CF树产生基本的聚类，再进行一或多遍扫描可以进一步改进聚类的质量。算法的计算复杂度是O（n）。实验表示BIRCH算法对数据集规模伸缩有线性的时间效率，且聚类质量较好。但是，由于CF树节点阈值限制，其聚类结果并不总是表达了自然聚类。而且，如果簇不是球形的，算法不会很好地工作，因为它用半径和直径的概念来控制聚类过程。
大多数聚类算法或者擅长处理球形和相似大小的聚类，或者在存在孤立点时变得比较脆弱。CURE解决了偏于球形和相似大小的问题，在处理孤立点上也更加健壮。CURE采用一种新的层次聚类算法，算法选择基于质心和基于代表对象方法之间的中间策略[25]。在CURE算法中，一个簇的代表点通过如下方式产生：首先选择簇中分散的对象，然后根据一个特定的分数或收缩因子向簇中心收缩。有算法的每一步，有最近距离的代表点对的两个簇会被合并。CURE算法的核心步骤描述如下[25]：
1）从源数据对象中抽取一个随机样本S。
2）将样本S划分为一组分块。
3）对每个划分局部聚类。
4）通过随机取样剔除孤立点。如果一个簇增长得过慢，就去掉它。
5）对局部的簇进行聚类，落在每个新形成的簇中的代表点根据用户定义的一个收缩因子a收缩或向簇中心移动。
6）用相应的簇标签来标记数据。
每个簇有多于一个代表点，使得算法可以适应非球形的几何形状。簇的收缩可以帮助控制孤立点的影响。因此，CURE对孤立点的处理更加健壮。而且，能够识别非球形和大小变化较大的簇。对于大规模数据集，它的伸缩性较好，且聚类质量不降低[25]。
有关数据挖掘算法及在视频分析中的应用的文章
- 详细阅读
-
K-Means 聚类算法优化简介详细阅读
算法9.1K－Means聚类选择一些类/组，并随机初始化它们各自的中心点，中心点是与每个数据点向量长度相同的位置。K－Means采用的启发式方式很简单，用下面一组图就可以形象地描述。图9－1K－Means的启发式方式(见彩插)......
2023-06-21
-
基于Spark的聚类算法实现详细阅读
Spark MLlib中的K-means算法使用Map分布式读取数据集，并存储在内存里。计算时，用Map键值对表示随机挑选出来的k个聚类中心，Spark的驱动器节点负责把数据发送到各个工作节点，以实现具体的计算任务。Spark MLlib不同于传统的机器学习工具，它提供了简单易用的API，特别是Spark能够高效地处理大数据，并且在迭代计算时具有较强的优势。......
2023-11-21
-
不同年份聚类结果比较分析详细阅读
2000年和2013年两次聚类分析的分类特点基本一致，分类结果有相似之处也有变化较为明显的地方，以下分析造成变动的因素所在。这一变化情况在2013年的聚类结果中反映地更加明显。即从全国纵向发展水平上看，2013年相较于2000年经济发展水平提高的同时老龄化程度加重，但是不同省份间变化的差异程度较大，2013年的分类结果说明经济发展水平和老龄化水平之间的正相关关系大大减弱。......
2023-08-10
-
利用聚类和异常值分析法识别黑点详细阅读
对纽约市交通事故进行空间热点分析时，选用聚类和异常值分析法对计算出的结果进行挖掘。H区域为西35大街和36大街在第五大道与第六大道中间的路段，从中午12时至下午5时，此区域为交通事故黑点路段。......
2023-06-15
-
音频检索：基于内容的特征提取与聚类详细阅读
对声音进行数字化处理得到的结果称为音频。对音频，需要通过听觉特征进行检索。音频有别于一般数据，本身是一种正弦波，检索前需要进行预处理，以提取音频特征或文本描述。基于内容的音频检索系统的第一步是先建立数据库对音频数据进行特征提取，将音频数据装入数据库的原始音频库部分，将特征装入特征库部分，通过特征对音频数据聚类，将聚类信息装入聚类参数库部分。......
2023-11-01
-
类弹丸聚能侵彻体释能模型的活性分析详细阅读
类弹丸活性聚能侵彻体化学能分布式释放过程如图3.3所示。爆轰波完全扫过活性药型罩后，罩体内压力及温度进一步升高，活性药型罩顶部发生明显形变，在轴线处发生翻转，形成类弹丸活性聚能侵彻体头部。基于以上假设，以侵彻体尾部端面中点为原点，建立二维平面物质坐标系，类弹丸活性聚能侵彻体化学能分布式释放计算模型如图3.4所示。在继续成形过程中，侵彻体中部及尾裙部分温度逐渐升高，相继发生激活。......
2023-06-18
-
试验数据分析与判断方法优化详细阅读
2）虽然试验结果是分析判断的依据，但试验的全过程分析更为重要。一般来说，试验方法正确，各项试验结果都在《规程》的规定范围内，则可以认为试验结果基本正确，电气设备绝缘为良好，可以投入运行。如果试验结果超过《规程》的规定范围或者被试设备没有标准可供参考时，首先考虑试验方法和试验结果的正确性，必要时进行复试验证。......
2023-06-27
相关推荐