在所有可能的项集中，有很多候选都不是频繁的。算法4.2Apriori算法伪代码FPGrowth方法使用一种增强的前缀树对数据D进行索引，以实现快速的支持度计算。FPGrowth将所有的项按照支持度的降序排列。FP树构建完成后，所有的频繁项集就可以从树中挖掘出来。基于频繁树模式的频繁集搜索方法见算法4.3。算法4.3FPGrowth算法伪代码......
2023-06-15
基于FP-growth的频繁项集挖掘算法
【摘要】：在借助数据结构存放中间结果来挖掘关联规则的算法中，FP-growth算法[89]效率较高，其中使用的树结构FP-Tree成为很多研究的基础。通过递归调用FP-growth的方法来直接产生频繁项目集。为方便后面叙述，表2.1中在第3列列出了每个事务中按降序排列的频繁项。第二次扫描数据库并构建FP-Tree。图2.6[例2.1]生成的FP-TreeFP-Tree的构造算法如图2.7所示。FP-growth算法以FP-Tree头表的倒序为计算顺序，从下至上递归搜索FP-Tree，逐步生成所有的频繁项集。图2.7FP-Tree的构造算法图2.8FP-growth算法
在借助数据结构存放中间结果来挖掘关联规则的算法中，FP-growth算法[89]效率较高，其中使用的树结构FP-Tree成为很多研究的基础。算法的重点还是在挖掘频繁项集的过程，分为两部分：
（1）通过两次扫描事务数据库，把每个事务所包含的频繁项目按其支持度降序压缩存储到FP-Tree中。
（2）通过递归调用FP-growth的方法来直接产生频繁项目集。这个过程不需要再扫描事务数据库，而仅在FP-Tree中进行查找即可，在整个发现过程中也不需产生候选项目集。
FP-Tree由两部分构成：头表和树。头表中节点由itemname、count和node_link 3个域组成，分别标识项目名、支持数和指向树中第一个同名节点的指针。树中节点由itemname、count、parent_link、node_link 4个域组成，分别标识项目名、计数、父节点的指针和指向树中下一同名节点的指针。通过以下例子来说明FP-Tree的构造过程。
【例2.1】（见文献[89]中的[例3.1]）：设有如表2.1所示的前两列事务数据库。令最小支持数为3。则FP-Tree的构造过程如下：
表2.1 示例事务数据库
（1）访问一次数据库，找出所有频繁1-项集，并按支持数降序排列，结果为：＜（f：4），（c：4），（a：3），（b：3），（m：3），（p：3）＞（“：”后面表示项目的支持数）。生成头表中的项，并将每项后的指针初始化为“null”。为方便后面叙述，表2.1中在第3列列出了每个事务中按降序排列的频繁项（Frequent items）。
（2）创建树的根节点并标记为null。第二次扫描数据库并构建FP-Tree。
取到第1个事务；析出其中的频繁项；降序排列；在根下创建树的第一个分支：＜（f：1），（c：1），（a：1），（m：1），（p：1）＞。
取到第2个事务；析出其中的频繁项；降序排列＜f，c，a，b，m＞。因为其前3项＜f，c，a＞与现在树中第一个分支的前3个节点重复，只需在树中把这3个节点的计数分别加1变成＜（f：2），（c：2），（a：2）＞；再给节点＜（a：2）＞增加一个子分支＜（b：1），（m：1）＞。
取到第3个事务；析出其中的频繁项；降序排列＜f，b＞。因为其第一项＜f＞与现在树中第一个分支的前一个＜（f：2）＞节点重复，只需树中把这3个节点的计数分别加1变成＜（f：3）＞；再给节点＜（f：3）＞增加一个子分支＜（b：1）＞。
取到第4个事务；析出其中的频繁项；降序排列＜c，b，p＞。因为其与现在树中的分支没有前端重复，所以给根节点增加一个子分支＜（c：1），（b：1），（p：1）＞。
取到第5个事务；析出其中的频繁项；降序排列＜f，c，a，m，p＞。因为其与现在树中最左分支完全重复，所以只需给这个分支的每个节点的计数加1，变为：＜（f：4），（c：3），（a：3），（m：2），（p：2）＞。
这个过程中随时将各新生成节点与头表中相应的项进行链接。最后生成的FP-Tree如图2.6所示。
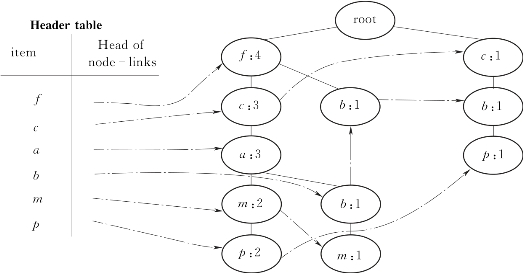
图2.6 [例2.1]生成的FP-Tree
FP-Tree的构造算法如图2.7所示。
可以看出，通过两次访问数据库，所有频繁项目的信息被存放到FP-Tree中。FP-growth算法以FP-Tree头表的倒序为计算顺序，从下至上递归搜索FP-Tree，逐步生成所有的频繁项集。其算法如图2.8所示。
FP-Tree在不损失事务信息的情况下，有效地压缩了数据库中数据，是迄今为止提出的较有效的数据结构，目前有许多研究都是基于这个结构的。
图2.7 FP-Tree的构造算法
图2.8 FP-growth算法
有关数据挖掘算法及在视频分析中的应用的文章
- 详细阅读
-
如何表示事务数据库中的频繁项集？详细阅读
图2.2事务数据库的4种表示形式项目向量；项目列表；Tid向量；Tid列表设X为I中某些项目的集合，简称为项集。如果项目集XT，则称事务T包含项集X，或称事务T支持项集X。频繁项集具有如下两个性质：如果X是频繁项目集，那么X的任何非空子集都是频繁项目集。还有相当多的学者研究了关联规则挖掘与关系数据库紧密结合的问题[71，72-88]，关联规则的结果评价标准问题[81]，挖掘系统的构架、交互方式及可视化问题[83]等。......
2023-06-16
-
基于聚类的全局特异数据挖掘算法详细阅读
设某一属性的所有值的数据集为S，其平均值为Smean。根据这些想法，提出一种基于聚类的全局特异数据挖掘方法。构架仍由挖掘特异属性和挖掘特异记录两个层次构成。从原则上讲可以采用任何基于距离的聚类算法对S进行聚类，采用的聚类算法的效果好，可以减少后续的计算量。图3.2SimC聚类算法可以看出，k是控制聚类半径Cd的。现在根据式（3.9）计算每个类的特异因子，记为CPF。显然，CPF越小的类，其中的元素是特异数据的可能性越小。......
2023-06-16
-
关联规则挖掘中的FP-tree算法及效果详细阅读
设数据集D被分割成分块D1，D2，...，Dn，全局最小支持数为minsup_count。因此，探索新的理论和算法来减少数据库的扫描次数和候选集空间占用，已经成为近年来关联规则挖掘研究的热点之一，典型的方法是FP-tree算法。......
2023-11-08
-
经典挖掘算法Apriori与关联规则详细阅读
Apriori算法[3]是单维、单层、布尔关联规则挖掘算法，是最简单形式的关联规则挖掘。该算法是挖掘产生布尔关联规则频繁项目集的经典算法，对关联规则挖掘研究有着重要影响。图2.3Apriori-gen算法Apriori算法调用Apriori-gen，生成所有频繁项集，如图2.4所示。Apriori算法假定数据库驻留在内存中。Apriori算法之后，学者们不断研究其改进算法及其他思想的关联规则挖掘算法，取得了很多成果。图2.4Apriori算法图2.5找出频繁项集L后生成关联规则算法......
2023-06-16
-
基于Spark的聚类算法实现详细阅读
Spark MLlib中的K-means算法使用Map分布式读取数据集，并存储在内存里。计算时，用Map键值对表示随机挑选出来的k个聚类中心，Spark的驱动器节点负责把数据发送到各个工作节点，以实现具体的计算任务。Spark MLlib不同于传统的机器学习工具，它提供了简单易用的API，特别是Spark能够高效地处理大数据，并且在迭代计算时具有较强的优势。......
2023-11-21
-
基于Weka的关联规则挖掘方法详细阅读
Weka工具的关联规则挖掘过程如图2-3所示。图2-4Weka选择函数设置Apriori算法的参数如下：car如果设为真，则会挖掘类关联规则而不是全局关联规则。delta以此数值为迭代递减单位，不断减小支持度直至达到最小支持度或产生了满足数量要求的规则。设置对规则进行排序的度量依据，可以是置信度、提升度、杠杆率、确信度。在Weka中设置了几个类似置信度的度量来衡量规则的关联程度，它们分别是，①Lift：P（A，B）/Lift=1时表示A和B独立。......
2023-11-08
-
基于W-O算法的谱估计方法详细阅读
对于双窗系统，EN不再恒等于1，但具有“倒余弦”形状，这样W-O分析谱中在每点都产生旁瓣。同古典谱估计方法相比，由于AR模型是一个有理分式，因而估计出的谱比古典谱估计法估计出的谱平滑。由式易知，X0在k=0时的权值为N，即阶数越高，W-O谱线分辨力越强。图6-9 传统信号加窗与W-O谱分析由图6-9可以看出，用W-O方法得到的信号频谱比用传统加窗方法具有更少、更低的旁瓣干扰。......
2023-06-23
相关推荐