如何表示事务数据库中的频繁项集？

2023-06-16 理论教育版权反馈

【摘要】：图2.2事务数据库的4种表示形式项目向量；项目列表；Tid向量；Tid列表设X为I中某些项目的集合，简称为项集。如果项目集XT，则称事务T包含项集X，或称事务T支持项集X。频繁项集具有如下两个性质：如果X是频繁项目集，那么X的任何非空子集都是频繁项目集。还有相当多的学者研究了关联规则挖掘与关系数据库紧密结合的问题[71，72-88]，关联规则的结果评价标准问题[81]，挖掘系统的构架、交互方式及可视化问题[83]等。

设I={i1，i2，…，im}是m个不同项目的集合。D是所有事务的集合（即事务数据库），每个事务T是一些项目的集合，T包含在I中，即T⊂I，并且每个事务可以用唯一的标识符Tid来标识。通常D是二维表，一维表示项目，另一维表示每个Tid事务所具有的项目情况，它有4种表示形式：项目向量（Item-vector）、项目列表（Item-list）、Tid向量（Tid-vector）和Tid列表（Tid-list），示例如图2.2所示[3，26，27]。

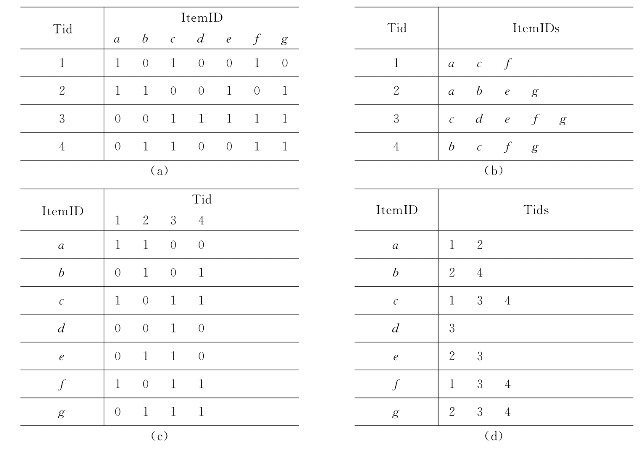
pagenumber_ebook=11,pagenumber_book=6

图2.2　事务数据库的4种表示形式

（a）项目向量；（b）项目列表；（c）Tid向量；（d）Tid列表

【定义2.1】设X为I中某些项目的集合，简称为项集（Item-set）。如果X中含有K个项目，即|X|=K，则称X为K-项集。

【定义2.2】如果项目集X⊆T，则称事务T包含项集X，或称事务T支持项集X。D中包含X的T的个数称为D对X的支持数，简记为count（X）。D中包含X的T的比率称为D对X的支持度，记为support（X），一般用百分比表示。如果用|D|表示D中T的总数，显然有：

【定义2.3】关联规则是形如：X⇒Y的蕴涵式，这里X⊂I，Y⊂I，并且X∩Y=Φ。称X为前件（antecedent），Y为后件（consequent）。称support（X⇒Y）=support（X∪Y）为此关联规则的支持度。关联规则X⇒Y的置信度是包含X∪Y的事务数与包含X的事务数的比值，记为confidence（X⇒Y），所以有：

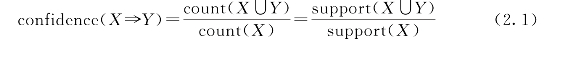
pagenumber_ebook=11,pagenumber_book=6

给定最小支持度阈值minsup和最小置信度阈值minconf，关联规则挖掘即在D中找出所有支持度≥minsup和置信度≥minconf的关联规则。

【定义2.4】若项集X的支持度不小于最小支持度，则称X为频繁项目集。若某一项目im满足最小支持度要求，则称im为频繁项目，所有频繁项目的集合称为频繁1-项集，记为L1；满足最小支持度要求的k-项集称为频繁k-项集，所有频繁k-项集的集合记为Lk。

给定最小支持度阈值minsup，频繁项集挖掘即在D中找出所有支持度≥minsup的频繁项集。频繁项集具有如下两个性质：

【性质2.1】如果X是频繁项目集，那么X的任何非空子集都是频繁项目集。

【性质2.2】如果X是非频繁项目集，那么X的任何超集都是非频繁项目集。

【定义2.5】若频繁项目集X的所有超集都是非频繁项目集，则称X为最大频繁项目集；所有最大频繁项目集组成的集合称为最大频繁集。

由上面的定义可知，最大频繁集已经隐含了所有频繁项目集。挖掘最大频繁集有效地减少了挖掘结果的数目，但是它不能反映其所有频繁项目子集的支持数信息。频繁闭项集（Frequent closed items）能减少挖掘结果的数目，同时保留了其项目子集的支持数信息，其定义如[定义2.6]。

【定义2.6】一个项目集X被称为是频繁闭项目集，如果X是频繁的，并且不存在任何X的真超集Y，使得support（X）=support（Y）。

自从在SIG MOD93会议[28]上第一次提出关联规则的概念以来，关联规则一直是众多学者研究的热点。其中，研究算法（包括挖掘频繁项集的算法）的文献可以有多种分类。可分为直接对源数据集进行挖掘的算法和借助数据结构来挖掘规则的算法[29，3041]；可分为挖掘一般频繁项集的算法和挖掘最大、闭频繁项集的算法[38，3953]；水平优先的算法和垂直优先的算法[54]；还有分布并行关联规则的挖掘算法[56]；挖掘带有约束条件的关联规则算法[40，55-70]；关联规则增量更新挖掘算法[35]等。还有相当多的学者研究了关联规则挖掘与关系数据库紧密结合的问题[71，72-88]，关联规则的结果评价标准问题[81]，挖掘系统的构架、交互方式及可视化问题[83]等。但是，数据挖掘乃至关联规则挖掘技术还没有成熟，要达到实用推广还需要做长期艰苦的探索。

如何表示事务数据库中的频繁项集？

相关推荐