计算机在生物医学中的视觉系统建模与仿真

6.5　视觉系统的建模与仿真

感觉系统是由感觉器官和与之相联系的神经系统构成的。概括地说，感觉器官包括眼、耳、鼻、舌、身。从生理学角度来说，遍布于身体各处的感觉器是组成感觉器官的基本单元。为人们所熟知的最明显的感觉有5种：视觉、听觉、味觉、嗅觉、触觉。

感觉系统是人类生活不可缺少的部分，同时也是人体与外界进行信息交换和相互作用的通道，因此，人们很早就开始研究感觉系统的机理。但那些早期的研究多为定性的粗略探索。到了20世纪初期，随着电子工业的崛起，给生理学研究注入了活力。为了避开人体系统的高度复杂性，研究者们选用鱼、蛙等低级动物为对象，对其光感受单元的电生理机理进行了大量的定量实验研究。同时，为了定量地分析实验结果并由此引出适当的推论，人们采用了建立数学模型的方法将实验结果引向深入。通过这些研究，人们发现，孤立地研究单一感受器不足以揭示感觉系统的机理，还必须将其与相邻的感受器单元以及与之相联系的神经网络的共同作用视为一个系统来考虑。

图6.4　眼睛光学系统示意图

在感觉系统中，最吸引人的是视觉系统。尤其是基于人工智能、计算机视觉、机器人学等领域的发展需要，如何深入地了解视觉机理并在机器上加以模拟和实现，成为一个迫切的任务。这方面的研究涉及生理学、心理学、工程技术等多个学科的知识，其研究的广度和深度是其他生理系统所无法比拟的。

视觉系统可分为两大部分，一是由眼球构成的光学系统，二是由视网膜及与之相联系的神经传导网络构成的视觉信息传递通路。眼球的光学系统如图6.4所示，它由角膜、房水液、晶状体和玻璃体组成。为了保证目标物的成像经由此光学系统后正好落在视网膜的中央，眼球在外眼肌的作用下能够进行中心部基本固定的旋转运动。

图6.5　视神经结构图

通过眼球的光学系统进入的光线将由视网膜转换成神经电信息。根据电子显微镜的观察，如图6.5所示，视网膜由三类细胞形成了纵向的信息传递通路，即：视细胞、双极细胞、神经节细胞，同时，还由水平细胞和无足细胞形成横向联系。视细胞又分为视杆细胞和视锥细胞。在人的视网膜上，视细胞的数目达6亿个。这些细胞的自身功能与它们之间的相互作用构成了对视觉信息的有效处理，因而成为视觉系统中最值得研究的部分。在这方面已经提出了许多有效的视觉信息处理模型，同时还有大量的工作仍在进行。

鉴于视觉系统在感觉系统中的地位，本节将着重介绍一些视觉系统的原理模型。但由视觉系统得出的理论和方法往往也适用于其他感觉系统。

6.5.1　瞳孔尺度控制模型

在生物控制论中，瞳孔的尺度随光照量的变化而改变，是一个典型的生理反馈控制系统，它可以自动调节投射到视网膜上的光强，如图6.6所示。其反馈途径大致如下：瞳孔是虹彩中心的一个小孔，光线通过它射到由光感受细胞组成的视网膜上，然后通过载有光强信息的传入神经，经过顶盖区中转，通向脑部的动眼神经核。传出的反馈通道分两路：一部分通过副交感神经，在睫状神经节处转换后去控制瞳孔括约肌的收缩；另一部分由交感神经传出，最后在上颈脊神经节转换后去支配瞳孔括张肌的活动。当输入光信号增强时，该系统就可自动改变瞳孔面积的大小，从而调节落在视网膜上的光量。对这样一个较为简单又具有典型意义的生理调节控制系统进行研究，将有利于进一步探讨各种复杂生理系统的控制机理。

图6.6　瞳孔反馈控制系统

（a）生理结构；（b）模型的功能单元组成

正是由于瞳孔尺度控制系统所具有的负反馈系统的典型特征，自20世纪50年代起，美国加州大学伯克利分校的Stark教授等人就开始对这一系统的特性进行较为深入的探讨。尤其令人感兴趣的是，这一系统的输入信号是光，这是一个容易控制的物理量，而系统的反应是瞳孔面积的变化，它正好在透明的角膜后面，可用光学方法进行测量，因此该系统被认为是人体中最容易研究的反馈系统，并且在研究中还可以将该系统的反馈回路断开或改变系统的增益。

图6.7　瞳孔反馈系统简化示意图

为简化问题，采用如图6.7所示的反馈系统。其变量定义如下：x为射入视网膜的光量；I为光强；y为瞳孔面积。在正常情况下，到达视网膜的光量正比于光强和瞳孔面积，故有：

而光量的增加又将导致瞳孔面积的减小，即有：

为了获得这一系统的定量特性，Stark等人完成了一个著名的瞳孔对光反射开环频率特性的实验，从中得出了这一系统的开环传递函数（s为拉普拉斯算子）：这个实验的基本做法如下：利用瞳孔直径仅在2～8mm间变化的事实，若用小于2mm的正弦调制光来通过瞳孔中心时，则瞳孔大小的变化不影响过光量的多少，从而实现了开环。在开环情况下，用不同频率的正弦调制光束为输入，以瞳孔面积为输出，则可获得系统的开环传递函数如式（6.4）。

Stark所做的上述工作是首次在人活体上完成的开环频率特性实验，其所得的模型可成功地预测瞳孔系统在小阶跃输入下的响应，以及当光束照射瞳孔边缘时而导致的瞳孔尺度振荡现象。尽管这是一个十分简单的模型，但仍然是有实际意义的。

在后来的几十年中，不断有人在Stark所做的早期工作的基础上继续研究瞳孔反射控制系统的特性。比如上海生理所的孙复川等人，为了能够模拟瞳孔的逃避现象和俘获现象，提出了如图6.8所示的瞳孔光反射模型。该模型在输入端引入lg环节来反映视觉感受器的对数特性，其中，上部用以描述单项速率的敏感性，下部则用以描述静态反应，因而高频动态信号将由上部通路通过，而低频的稳态信号则由下部传递。在这两部分之间引入了一个称为IPC（Internal Parameter Control，参数控制）的机制，用以改变上下两部分的增益，而这一改变取决于瞳孔的大小，因而该模型又称之为固有参数调节模型（Internal Parameter Adjustment Model，IPAM）。

图6.8　瞳孔光反射模型

通过对多个实测数据进行优化拟合，图6.8中模型的参数值确定如下：

图6.9　瞳孔光反射模型的实验测定

利用这一模型可模拟不同初始状态下的瞳孔光反射反应，孙复川等人所得的模型仿真和实验测定结果如图6.9所示，图中实线为仿真结果与实际测量结果吻合得很好。

6.5.2　视细胞模型

视觉系统中能量转换的基本单元就是视细胞。经过多年研究，人们发现，视细胞内的能量转换过程是由其内某种称为视色素的物质所引发的。当视细胞吸收光量子时，视色素就会发生称为“漂白”的光化反应，并产生某种化学物质。而细胞膜在这种化学物质的作用下会发生离子通透性的改变，使细胞极化，从而将接收到的光信息转换为电信息。

1968年，Rushton和Henrry发现，在光的作用下，视色素一方面产生漂白效应，与此同时，又存在再合成过程，其中视色素漂白的速率与入射光强度I成正比，而再合成速率与已经漂白的视色素的量成正比，综合这两个过程，可建立如下观色素的动态模型：

图6.10　视细胞等效电路

式中，s——没漂白的视色素的比例；

a，b——比例系数。

尽管这是一个十分简化的模型，人们仍用它来推测在某种光照下的视色素的状态。

从视色素发生光化学反应到视细胞产生动作电位的详细机理尚待探讨，然而在光的作用下，视细胞膜的电阻上升现象已通过测量观察到了，这种现象可用图6.10中的等效电路来模拟，即用钠离子通透性改变来描述。

若令无光照时的视细胞膜电位为V（0），相应的膜电阻为I_Na（0）和I_K（0），则当用强度为I的光照射时，膜电位的变化量可由图6.10所示电路计算出，即：

Korenbrot等人通过实验发现，视细胞膜电阻的变化量与已漂白观色素的比例（1-s）成正比，结合式（6.5）和式（6.6），可得视细胞的动作电位v与光强的关系为：

式中，σ=b/a；

v_max——当光强趋于无穷大时的动作电位极大值。

式（6.7）中的关系后来为许多人的实验所证实。但在进一步的深入研究中，人们更一般地用下式取代式（6.7）：

经实验测定，n的值在0.7～1.0范围内，且与实验时所用刺激光的持续时间有关。当采用持续时间为100 ms左右的闪光时，n=1.0；而若用持续时间为2s的闪光时，n=0.7。(www.chuimin.cn)

为了进一步阐明式（6.8）的含义，可将其改写为：

由此式可知，当取光强的对数为横坐标时，则动作电位为用双曲函数th x所表示的“S”形饱和曲线。其中常数σ确定了动态范围的位置，常数n则确定了动态范围的幅度，即当n增大时，曲线将平行向右移动，其形状却保持不变。这样一种特性在感觉系统中是较多见的。

6.5.3　侧抑制模型

上一节我们介绍了单个视细胞将接受到的光信息转换为神经电信号的特性及其研究用的模型。那么，这种由单个感受器所形成的神经电信息是否就直接传送给大脑了呢？其实不然。经过多年的研究，人们发现单个感受器可检测出外界刺激的时域变化，而大量感受器之间的相互作用则可起到检测外界刺激的空间变化的作用。由于这种感受器网络中的相互作用是抑制性的，故又称这种相互作用为侧抑制。

侧抑制的概念是由美国洛克菲勒大学的教授H.K.Hartline提出的。自20世纪30年代初起，他就一直致力于视觉和视网膜的研究，并在对鲎眼的研究中发现了侧抑制现象。即当测试小眼的邻近小眼也受到光照时，测试小眼的反应将被削弱；而若切断它们之间的联系，刚这种作用将不复存在。正是由于Hartline提出的侧抑制和感受野这两个感觉系统的重要概念，他于1967年获得了诺贝尔生理医学奖。

为了简化问题，我们先从两个相邻感受器的侧抑制入手，然后再推广到多个感受器网络的情况。

两个感受器单元之间的相互抑制性作用可通过图6.11来说明。图中，上部球形代表细胞体，下部杆状部分代表轴突，兴奋性脉冲将由标有×号处产生，并沿轴突向下传播，同时又将通过分枝对其相邻的细胞产生抑制。当抑制作用在脉冲产生点上部时，如图6.11（a）所示，称为循环性抑制；若其作用如图6.11（b）所示，则为非循环性抑制。

若令e₁和e₂代表两个感受器单元在割断与其他单元的联系时的刺激响应水平，那么，当存在两个单元之间的侧抑制作用时存在如下关系：

式中，r_l，r₂——在树抑制作用下两个感受器的实际响应水平；

K₁₂（K₂₁）——2号（1号）感受器对1号（2号）响受器作用的“抑制系数”；

图6.11　感受器间的相互抑制示意图

（a）循环性抑制；（b）非循环性抑制

图6.12　多感受单元间的抑制模型

（a）顺方向性抑制回路；（b）反方向性抑制回路

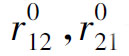——对应于抑制起作用的阈值。

从生理意义上考虑，还应有K_ij≥0，且当r_i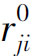＜时，K_ij=0，即若抑制作用没有达到阈值时将不起作用。同时，由于不存在负的神经发放水平（以脉冲发放频率计量），故若抑制性作用过强时，即当e_i＜K_ij（r_i-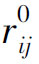）时，应取r_i=0。

当有n个感受单元相互作用时，其抑制模型如图6.12所示，图6.12（a）为顺方向性抑制回路，图6.12（b）是反方向性抑制回路。所谓顺方向性又称为前馈型或非循环式，而反方向性又称为反馈型或循环式。研究结果表明，在脊椎动物的视觉系统中，从末梢到中枢之间，都存在着不同形式的侧抑制机制，既有前馈型的，又有反馈型的。但人们研究得较多的是反馈型侧抑制网络，其原因可能是由于实验对象多为鲎一类的节肢动物，它的侧抑制属于反馈型的。

Hartline等人在实验中发现，对于视觉感受器来说，若其相邻的感受器受到光照的数目越多，则来自外周的对受试单元的抑制作用就越强，这表明侧抑制网络具有空间总和的作用。因此，为反映这样一种特性，我们可将式（6.10）和式（6.11）推广至任意n个感受器单元的侧抑制网络，即有：

式中各项的意义与式（7.10）和式（7.11）中一样。其中条件i≠j是假定不存在自抑制。为了保证r_i≥0和避免出现负抑制，可将上式重写为

式（6.13）就是感觉系统侧抑制网络的基本数学模型，尽管这是一个简化的模型，但实验证明，这一模型的确可以描述感受器单元网络的抑制性相互作用。同时，实验结果还表明，这种相互作用的强弱与这两个相互作用单元间的距离成反比，也就是说，邻近的感受器之间的抑制系数K_ij较大，但一般说来，这种抑制性作用在两个方向上并不一定相等，即K_ij不一定等于K_ji。

1963年，Hartline与其合作者Ratliff等对上述侧抑制网络模型进行了定量的检验。实验中，他们选用了三个相互作用的小眼，分别用A，B，C标志。实验首先对这三个小眼分别进行光照，并记录下其反应值，即确定e_A，e_B和e_C；然后，再对这三个小眼两两一组进行光照反应测量，从而可确定抑制系数K和阈值r⁰。根据这些值，则可由模型（6.13）计算出这三个单元同时受到光照时各自的反应，同时，也可由实验测定三个小眼全部在一起受到光照时的实际反应。计算结果和实验结果及所确定出的模型参数由图6.13给出，图中，横坐标为实验观测值，纵坐标为模型预测值，由图可见，两者基本吻合，从而证实了模型的有效性。

图6.13　网络抑制模型的参数实验结果

6.5.4　感受野模型

感受野是Hartline等人提出来的感觉信息处理系统的另一个重要概念。与上一节叙述的侧抑制作用相比，感受野的结构和功能更为复杂。Hartline最初定义的某个感觉细胞的感受野是指视网膜上用小光点的给光和（或）撤光能引起这个感觉细胞反应的区域。一般称给光反应为on反应，而称撤光反应为off反应。相应地，发生on反应的感受野称为on区，而发生off反应的感受野称为off区。如果某一部分感受野既能引起on反应，又能引起off后应，则称之为on-off区。

自从20世纪30年代Hartline等人对鲎的感受野进行了初步探索后，引起许多研究者的兴趣。此后的几十年中，大量的理论和实验工作一直在进行，其中，特别值得提出的是Hubel和Wiesel证明了视觉系统不同层次上的细胞对不同的几何特性有选择性反应。他们凭借在猫和猴的视觉系统上所完成的出色的工作获得了1981年的诺贝尔生理医学奖。所有这些研究工作都为进一步深入研究感觉系统机理积累了丰富的资料。在此基础上，亦出现了许多试图描述和概括感受野的功能和性质的数学模型。

1965年，Rodieck在电生理和组织学基础上最早提出了一个较完善的感受野数学模型。他的模型是建立在当时获得的有关感受野特性的基础上的，这些实验事实主要有：

图6.14　感受野模型

（a）on中心型；（b）off中心型

①猫等动物的感受野呈圆形对积分布，其中心既有on型又有off型，相应地称之为on中心型和off中心型。

②邻近的感受野互相重叠，因而在此两者交界区域既有on反应，又有off反应，形成on-off区。

③反应敏感性在中心处最高，高中心越远，敏感性越低。这种中心对称形感受野的中心部分称为中心区，其外侧称为外周区，因而总括起来称为“中心—外周”型感受野，如图6.14所示。图6.14（a）为on中心型，图6.14（b）为off中心型。

基于上述事实，Rodieck提出，“中心—外周”型感受野是两种感受野在空间上重叠的结果，其中之一范围较小而强度较大，另一个范围较大而强度较小。若假设这两种感受野对神经结细胞影响的权重都为高斯分布的，如图6.15所示，其中a为兴奋性反应的空间分布，b为抑制性反应的空间分布，则其整体反应可用这两个高斯函数之差来表示，如图6.15所示，即用一个墨西哥草帽形的曲面来描述同心圆结构的感受野的兴奋性强度的空间分布。

图6.15　感受野对神经结细胞影响的权重分布

关于感受野方面的模型，除了本书中所述数学模型及其计算机仿真工作外，还有各种电子模型，即用电子器件构造的模型，但其基本思路是一样的。由于实际感受野的复杂性，至今仍有许多人致力于这方面的工作。

【注释】

[1]1英尺=0.3048m