复习初三几何综合题，四解题模型式概括教学案例

2024-07-27 百科知识版权反馈

【摘要】：四解题模型式概括教学案例在复习初三几何综合题时，有这样一类对角互补的四边形中的问题：1．教师提出问题：如图8—15，在四边形ABCD中，∠B＋∠D＝180°，AC平分∠DAB，∠DAB＝60°，你可以得到哪些结论？这就是明确了如果图形中具有这样的条件，即可运用此解题模型。所以，教师引导学生学会提炼解题模型，是培养学生逻辑概括能力的重要方面。

四　解题模型式概括

教学案例

在复习初三几何综合题时，有这样一类对角互补的四边形中的问题：

1．教师提出问题：如图8—15，在四边形ABCD中，∠B＋∠D＝180°，AC平分∠DAB，∠DAB＝60°，你可以得到哪些结论？

学生通过画图、计算、探究可得到：

（1）BC＝DC。

图8—15　四边形ABCD

（2）AB＋AD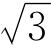＝AC。

2．思考：若在四边形ABCD中，∠B＋∠D＝180°，BC＝DC，∠DAB＝60°，则：（1）AC平分∠DAB，（2）AB＋AD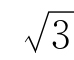＝AC是否还成立？

3．再思考：若在四边形ABCD中，BC＝DC，∠DAB＝60°，AC平分∠DAB，则：（1）∠B＋∠D＝180°，（2）AB＋AD＝AC是否还成立？

4．拓展问题：已知∠MAN，AC平分∠MAN，则：

（1）在图8—16中，若∠MAN＝60°，∠ABC＋∠ADC＝180°，则AB＋AD＝AC。

（2）在图8—17中，若∠MAN＝120°，∠ABC＋∠ADC＝180°，则AB＋AD＝AC。

（3）在图8—18中，若∠MAN＝90°，∠ABC＋∠ADC＝180°，则AB＋AD＝AC。

（4）试探究，若∠MAN＝α（见图8—19，0°＜α＜180°），∠ABC＋∠ADC＝180°，则AB＋AD＝AC（用含α的式子表示）。

图8—16　∠MAN＝60°

图8—17　∠MAN＝120°

图8—18　∠MAN＝90°

图8—19　∠MAN＝α

通过以上四个问题的自主解决，教师可引导学生回顾总结：这几个图形可以通过两种方式添加辅助线解决：（1）做双高构造轴对称（见图8—20）。（2）构造等腰三角形（见图8—21）。

图8—20　做双高构造轴对称

图8—21　构造等腰三角形

教师应进一步引导学生思考：为什么可以有这两种做法？第一种做法是由已知条件中的角平分线想到的，因为角平分线所在的直线是角的对称轴，所以可以利用它构造轴对称三角形。而角平分线定理是关于两个轴对称的直角三角形的，所以做双高应用角平分线定理。

第二种做法首先是由AB＋AD想到补短，得到某一条线段长度恰好等于AB＋AD，进而猜想到是将△ABC绕点C旋转到△EDC的位置。为了证明条件充分，辅助线定为构造等腰△ACE，这样可以得到三角形全等的条件。

总结解题方法之后，教师要再引导学生得到题目的本质特征，即四边形对角线平分一个内角（这是做辅助线的根本原因）、对角互补（以保证三角形全等）。这就是明确了如果图形中具有这样的条件，即可运用此解题模型。

接下来进行实践应用：

1．正方形ABCD中，点O是对角线AC的中点，P是对角线AC上一动点，过点P做PF⊥CD于点F，如图8—22，当点P与点O重合时，显然有DF＝CF。

（1）如图8—23，若点P在线段AO上（不与点A、O重合），PE⊥PB且PE交CD于点E。

①求证：DF＝EF。

②写出线段PC、PA、CE之间的一个等量关系，并证明你的结论。

（2）若点P在线段OC上（不与点O、C重合），PE⊥PB且PE交直线CD于点E。请完成图8—24并判断（1）中的结论①、②是否分别成立？若不成立，写出相应的结论。

（所写结论均不必证明。）

图8—22　P与O重合

图8—23　P在线段AO上

图8—24　P在线段OC上

2．已知∠AOB＝90°，OM是∠AOB的平分线，按以下要求解答问题：

（1）将三角板的直角顶点P在射线OM上移动，两直角边分别与边OA、OB交于点C、D。

①在图8—25中，当OP＝4时，求证：四边形PCOD的面积为定值。

②在图8—26中，点G是CD与OP的交点，且，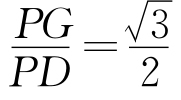

（2）若OD＝3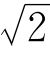，且满足∠GDO＝30°，求OP的长。（图8—27为备用图。）

若OP＝4，PD＝3，求OD的长。

图8—25　当OP＝4时

图8—26　当点G是CD与OP的交点时

图8—27　备用图

逻辑辨析

在目前的中学教学中，学生埋头于题海的现象仍然相当严重地存在。学生起早贪黑地做完一道题又做一道题，在六年的中学学习中，每位学生大概要做成千上万道题。虽然如此辛苦，但只要题目稍作变化，很多学生就感到不会应对了，于是在考试时仍然考不出好成绩。这是为什么？根本原因在于，题海战术使学生的思维陷于个别性、零散性、孤立性的状态。他们没有学会对这一系列看似个别、零散、孤立的习题进行思维的加工，从中提炼概括出具有普遍性的、相互联系的内容，他们没有去发现其中规律性的东西。其实，每一学科中可以做的习题，不管在表现形式上如何千变万化，都有一些普遍性的规律。作为教师，就是要引导学生从个别性、零散性、孤立性的思维中摆脱出来，把普遍性的内容提炼概括出来，掌握每一种类型题目的解题规律。这种从千变万化的众多习题中提炼概括出来的普遍性、规律性内容，就构成了解题模型。例如，物理学中，在做有关运动与力方面的习题时，我们就可以把众多的题目概括为如下几种解题模型：追及、相遇模型，先加速后减速模型，斜面模型，挂件模型，弹簧模型等。所以，教师引导学生学会提炼解题模型，是培养学生逻辑概括能力的重要方面。

在这个教学案例中，教师先给出题目让学生自己动手解决，再引导学生反思总结解决过程，抓住此类问题的本质，概括出解题模型。

由此可以得到概括解题模型的一种教学方式：

（1）由几道具有相同本质的题目引入，师生共同或学生自主探究解决。

（2）反思几道题目的解决过程，利用不完全归纳总结出解题模型。

（3）利用学科知识进行演绎推理，分析此模型的合理性及所需背景条件。

（4）总结分析此类题目的本质特征或条件。

（5）将解题模型应用到具体题目中，深入体会，灵活运用。

知识链接

美籍匈牙利数学家波利亚曾著有《怎样解题》、《数学的发现》、《数学与猜想》等，它们被译成多种文字，广为流传。波利亚主张数学教育的主要目的之一是发展学生的解决问题的能力，教会学生思考。他1944年在美国出版了《怎样解题》，其中“怎样解题”表总结了人类解决数学问题的一般规律和程序。⁽¹¹⁾

他在《怎样解题》一书中提出的包括“弄清问题”、“拟订计划”、“实现计划”和“回顾反思”四大步骤的解题全过程的解题表，实际上就是一个最基本的解题模型，书中还提出了20个“需要独创性和别出心裁”去解决的问题，希望通过解决这些问题“揭示出解答的关键性念头”⁽¹²⁾，也就是提炼概括出解题的一般规律，形成解题模型。这对数学解题研究有着深远影响。

此书已被译成至少17种语言广为传播，可说是一部现代数学名著。他随后又写了两部这类书：其一是1954年出版的两卷本《数学与合情推理》，再次阐述了在《怎样解题》以及其他论文中所提到的启发式原理，被译成6种语言；其二是出版了两卷本《数学的发现》，1962年出版第一卷，1965年出版第二卷，1981年又合成一卷再版，被译成8种语言。这些著作一经出版，立刻在美国引起轰动，很快风行世界，使波利亚成为当代的数学方法论、解题研究与启发式教学的先驱。70与80年代，中国陆续翻译出版了波利亚的上述著作，随之在中国掀起一股“波利亚热”，促进了中国数学教学的改革，提高了中国数学解题研究的水平。

1959年，波利亚以“数学作为学习合情推理的学科”为题，在美国《数学教师》杂志上发表论文，提出“合情推理”概念，认为在数学研究与数学教学中合情推理占有很重要的地位。随后在《数学与合情推理》第二卷中，进一步阐述了合情推理及其模式。波利亚的合情推理是指借助归纳、模拟、限定、推广、猜测、检验等思维活动来认识事物、发现真理的推理形式。例如，我们知道，在充分条件下，如果命题A可推出命题B，且命题A是真的，则命题B必真。反过来，如果命题B是真的，那么能否推出命题A为真呢？演绎推理认为不能必然推出命题A真。但波利亚认为，B真对增大A真的可能性会产生影响，他认为若A可推出B₁、B₂等，且B₁、B₂等均为真，则A真的可靠性将大大提高。由于他在合情推理中使用了“命题的可靠性”概念，因此，很想利用概率论方法来研究合情推理，但是他遇到了困难。虽然如此，这仍不愧为对数学方法论的重要贡献。⁽¹³⁾

扩展延伸

【数学】

利用平移和轴对称变换求线段和（差）最值。(www.chuimin.cn)

图8—28　直角坐标系

如图8—28，在直角坐标系中有四个点A（－6，3），B（－2，5），C（0，m），D（n，0）。

（1）要使△ABC周长最短，求C点坐标。

（2）要使四边形ABCD的周长最短，在图中做出符合要求的C、D两点（简要叙述做法），并求出m、n的值。

教师引导学生分析：在第一题中，因为AB的长度固定，当且仅当AC＋BC最短时，△ABC周长最短；AC＋BC最短，可以联想到“两点之间，线段最短”。怎样才能使AC＋BC是AB两点之间的线段呢？需要做其中一个点关于y轴的对称点，如B点的对称点B′。由此，BC转化为B′C，当C点在线段AB′上时，AC＋B′C即AC＋BC最短，则可以由两直线交点确定C点的位置。

变式一：在直角坐标系中，A（－6，3），B（－2，5），长为2的线段CD在x轴上滑动，问CD滑到什么位置时，四边形ABCD的周长最短？

变式二：在直角坐标系中有三个点A（－6，3），B（－2，5），E（n，0），长为1的线段CD在y轴上滑动，问CD滑动到什么位置时，五边形ABCDE的周长最短？

变式三：在直角坐标系中有两个点A（－6，3），B（－2，5），长度为2的线段CD在y轴上滑动，长度为1的线段EF在x轴上滑动，问当线段CD、EF滑动到什么位置时，六边形ABCDEF的周长最短？

通过几道问题的解决，教师可以引导学生概括出：要想求线段和的最小值，可以将两定点平移或对称，将线段和转化为两定点间的折线和，利用“两点之间，线段最短”确定最短距离。

实战练习：在平面直角坐标系xOy中，关于y轴对称的抛物线y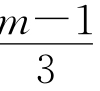＝－ x ²＋（m－2）x＋4m－7与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，P是这条抛物线上的一点（点P不在坐标轴上），且点P关于直线BC的对称点在x轴上，D（0，3）是y轴上的一点。

（1）求抛物线的解析式及点P的坐标。

（2）若E、F是y轴负半轴上的两个动点（点E在点F的上面），且EF＝2，当四边形PBEF的周长最小时，求点E、F的坐标。

这个教学案例是通过解决问题概括出求线段和的最值的一般方法，类比此类问题还可以得到线段差的最值。与前一个案例略有不同，由于题目是学生难以入手的，所以由老师引导学生进行分析得到一个解决方法（但并没有形成解题模型），学生再以此思路解决此类较复杂的题目，最后进行总结概括，抓住题目的本质特征及解决的主要思路，这样做一是为了让学生形成解题模型，二是加深学生对解题思路的理解，以更好地应用。

【物理】

初三物理教学中，常常要涉及电学综合题的讲解和分析，这也是中考的压轴题之一。

如图8—29所示的电路中，电源两端电压U不变，灯L上标有“4V 2W”字样，不计灯丝电阻受温度的影响。当开关S₁闭合、S₂断开时，灯泡正常发光，电压表V₁与V₂的示数之比为6∶7，电路消耗总功率为P；当开关S₁、S₂均闭合时，电路消耗的总功率改变ΔP，且ΔP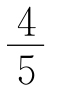＝ P。求：

（1）当开关S₁、S₂均闭合时，电路中的电流；

（2）电阻R₁与R₂的阻值；

（3）当开关S₁、S₂均闭合时，电阻R₂在1min内消耗的电能W。

图8—29　实物图

由于是难度较高的综合题，应由老师引导学生解决。首先认真仔细阅读题目，找到题目中的两种状态，即“开关S₁闭合、S₂断开”和“开关S₁、S₂均闭合”。

然后在两种状态下，去掉无关的实物，利用所学的流向法、节点法分析电路，画出等效电路图：当开关S₁闭合、S₂断开时，电路如图8—30所示，电压表V₁与V₂的示数分别为U 1、U ₂，电路中的电流为I；当开关S₁、S₂均闭合时，电路如图8—31所示，此时电路中的电流为I′。也就是将实际问题抽象概括出物理模型。

图8—30　等效电路图甲

图8—31　等效电路图乙

根据两个电路图和题中所给数据写出关系式，注意找出某个不变的物理量，如某个电阻或总电压、串联电路中的电流、并联电路中的电压等。

最后找出各个关系式之间的关系，要充分利用题目中的已知或已经求出来的比例达到减少未知量的目的，避免试图将每个物理量都求出来。

（1）小灯泡正常工作时的电阻电流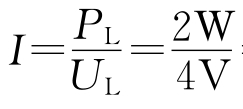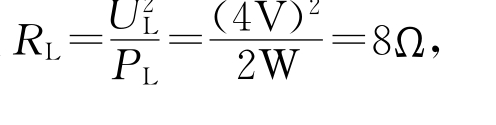＝0．5A，P＝UI，P′＝UI′，依题意ΔP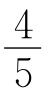＝ P，P′＞P，则P′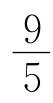＝ P，UI′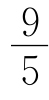＝UI，I′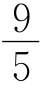＝ I，解得I′＝0．9A。

（2）由图8—30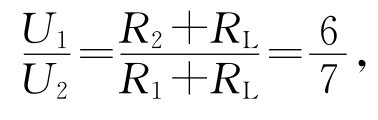解得6R₁－7R₂＝8Ω（8—4）

解得R₁＋R₂＝10Ω（8—5）

由（8—4）、（8—5）两式解得R₁＝6Ω，R₂＝4Ω。

（3）电阻R₂在1min内消耗的电能

W＝I′²R₂t＝（0．9A）²×4Ω×60s＝194．4J。

在解决完此问题后，可以回顾解题思路，概括解题模型：

看（认真仔细地阅读题目）；画（正确画出等效电路图）；写（就每一个电路图写出关系式）；找（找出各个关系式之间的关系）。

实战练习：

如图8—32所示，电源两端电压U保持不变。当开关S₁闭合、S₂断开，滑动变阻器接入电路中的电阻为R _A时，电压表的示数为U ₁，电流表的示数为I₁，电阻R₁的电功率为P₁，电阻R _A的电功率为P _A；当开关S₁、S₂都闭合，滑动变阻器接入电路中的电阻为R _B时，电压表的示数U ₂为2V，电流表的示数为I₂，电阻R _B的电功率为P _B；当开关S₁闭合、S₂断开，滑动变阻器滑片P位于最右端时，电阻R₂的电功率为8W。已知：R₁∶R₂＝2∶1，P₁∶P _B＝1∶10，U ₁∶U 2＝3∶2。求：