课堂逻辑：全称量词辨识

2024-07-27 百科知识版权反馈

【摘要】：二辨别量词：全称量词教学案例在人教版义务教育课程标准实验教科书《数学》七年级上册的“绝对值”一课中，老师设计了如下环节，得出绝对值的非负性：教师提出问题：请把1．5，0，－2．3分别标在数轴上，并求出它们到原点的距离。常见的全称量词有“所有”、“凡”、“一切”、“任意一个”、“全体”、“每一个”、“任给”等，用符号“A”表示。含有全称量词的命题叫作全称命题。

二　辨别量词：全称量词

教学案例

在人教版义务教育课程标准实验教科书《数学》七年级上册的“绝对值”一课中，老师设计了如下环节，得出绝对值的非负性：

教师提出问题：请把1．5，0，－2．3分别标在数轴上，并求出它们到原点的距离。

教师给出绝对值的几何意义：数轴上表示数a的点到原点的距离，叫作a的绝对值，记作｜a｜。

教师请学生把下列各数标在数轴上，并求出它们的绝对值：

由学生观察结果并得到绝对值的代数定义：

一个正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0。可表示为：

教师请学生观察例题中各数求绝对值后的结果，猜想任何一个有理数的绝对值是什么数，并利用绝对值的几何或代数定义说明自己的猜想。

绝对值的性质：一个数的绝对值是非负数，即｜a｜≥0。

可从两个角度说明此性质的正确性。（1）几何定义：由于绝对值是一个距离，而距离是非负的，所以｜a｜≥0；（2）代数定义：有理数分为正有理数、负有理数、零，正数的绝对值是它本身，是正的；负数的绝对值是它的相反数，是正的；零的绝对值是零。所以，一个数的绝对值是非负数。

在这个教学片段中，绝对值的几何意义给出后，由学生观察求正负数及零的绝对值的结果，并猜想得出绝对值的非负性，运用了完全归纳推理。这就是说，对于某个特定的集合，如果其中的所有元素都满足某一性质，那就说明了某个全称命题（肯定或否定）的正确性。

常见的全称量词有“所有”、“凡”、“一切”、“任意一个”、“全体”、“每一个”、“任给”等，用符号“A”表示。含有全称量词的命题叫作全称命题。

全称命题“对M中的任意一个x，有p（x）成立”可用符号“A x∈M，p（x）”表示，读作“对任意x属于M，有p（x）成立”。

在利用几何定义说明性质的正确性时，用到了三段论，即直言三段论或性质命题三段论，它是由两个包含着一个共同项的性质命题为前提，从而推出一个新的性质命题为结论的间接推理。这里具体为：

距离是非负的；

绝对值是距离；

所以绝对值是非负的，即｜a｜≥0。这是由两个包含着一个共同项“距离”的性质命题为前提，从而推出一个新性质命题“绝对值是非负的”为结论的性质命题推理，因而是三段论。

在这个最基本的三段论中，有且仅有“距离”、“非负的”、“绝对值”三个变项，而且每个变项都重复出现一次。在结论中做主项的“绝对值”叫小项，一般用“S”表示；在结论中做谓项的“非负的”叫大项，一般用“P”表示；只在两个前提中出现的那个共同的词项“距离”叫中项，用“M”表示。其结构可表示为如图4—3的形式：

图4—3　三段论结构

知识链接

在逻辑学中，性质命题实际上可归为对主项与谓项外延间关系的反映。A、E、I、O命题的真假，就取决于它们所反映的主项与谓项外延间的关系是否符合实际。主项与谓项外延间的关系不外乎以下五种（见图4—4、图4—5、图4—6、图4—7、图4—8）：

图4—4　全同关系

图4—5　真包含于关系

图4—6　真包含关系

图4—7　交叉关系

图4—8　全异关系

按照这五个图形所示的主、谓项外延间的各种关系，就可确定A、E、I、O四种命题的真假情况。

A命题也就是具有全称量词的肯定命题，反映了主项与谓项具有包含于关系，当且仅当S类与P类实际上具有图4—4或图4—5所示的关系之一时，它是真的，否则是假的。例如：（1）所有商品都是用来交换的劳动产品。（2）所有大学生都是共青团员。

例（1）中的“商品”与“用来交换的劳动产品”的外延之间，具有图4—4所示的关系，因而这个A命题是真的。而例（2）中的“大学生”与“共青团员”的外延之间不具有图4—4、图4—5所示关系，而是图4—7所示关系，因而这个A命题是假的。

E命题也就是具有全称量词的否定命题，反映了主项与谓项具有全异关系（或不相容关系），当且仅当S类与P类实际上具有图4—8所示关系时，它是真的，否则是假的。例如：（1）所有马克思主义者都不是有神论者。（2）所有工具都不是天然的。

例（1）中的“马克思主义者”与“有神论者”的外延之间具有图4—8所示的关系，因而这个E命题是真的，而例（2）中的“工具”与“天然的”的外延之间不具有图4—8所示关系，而是图4—7所示关系，因而这个E命题是假的。

数学命题、定理大多是具有全称量词的命题，说明其正确性时需要推理证明，说明其错误性时则只需要举出一个反例。美国数学家B．R．盖尔鲍姆和J．M．H．奥姆斯特德指出：“数学由两大类——证明和反例组成。而数学发现也是朝着两个主要目标——提出证明和构造反例。从科学性来讲，反例就是推翻错误命题的有效手段。从教学上而言，反例能够加深对正确结论的全面理解。”⁽¹⁾

扩展延伸

【物理】

物理学中有很多定律，都反映了物体运动的一般规律，其中就包含或隐含着全称量词。

如下面针对人教版普通高中课程标准实验教科书《物理》（必修）第二册中“万有引力定律”一节的教学设计：

通过上节的分析，我们已经知道了太阳与行星间的引力规律，那么行星为什么能够绕太阳运转而不会飞离太阳？因为行星与太阳间的引力提供行星绕太阳近似圆周运动的向心力，从而使得行星不会飞离太阳。

行星与太阳间的引力与什么因素有关？行星与太阳间的引力F与太阳和行星之间的距离r、行星质量m和太阳质量M有关。(www.chuimin.cn)

可以根据哪些已知定律推导出太阳与行星间的引力遵从什么样的规律？根据开普勒行星运动第一、第二定律和牛顿第三定律推出太阳与行星间的引力遵从的规律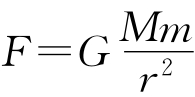：。公式中的G

是比例系数，F是太阳和行星之间的引力，正是这一引力使得行星不能飞离太阳。

那么大家是否想过，又是什么力使得地面的物体不能离开地球，总要落回地面呢？为了研究这个问题，下面我们继续来体验一下牛顿发现万有引力定律的思维过程。

教师演示：将塑料制成的且内部空心的苹果置于某位学生头顶上方不远处，静止释放。

教师引导学生思考：

（1）苹果为什么只砸向这位同学，而不砸向其他同学呢？

这是由于重力方向竖直向下，苹果在其重力作用下，在这位同学头顶正上方做竖直向下的自由落体运动。

（2）那么苹果受到的重力又是怎么产生的呢？

这一重力是由于地球对苹果的吸引而产生的。

（3）地球对苹果的引力和太阳对行星的引力是否根本就是同一种力？若是这样，物体离地面越远，其受到地球的引力就应该越小，比如我们爬到高山上时，是否察觉到重力减小了？为什么？

上述两种引力可能是同一种力。我们在山上并没有感到重力明显减弱，可能是因为还不够远。

（4）这样的高度比起天体之间的距离来说，简直太小了。如果我们再往远处设想，物体延伸到月球那么远，将会怎样运动？

可能这个物体会像月球那样绕着地球运动。

于是我们可以提出这样的猜想：太阳与行星、地球与月球、地球与地面上物体之间的作用力，也许真是同一种力，遵循相同的规律。假定上述猜想成立，月球和苹果的地位相当，则地球对月球的力与地球对苹果的力应该同样遵从“平方反比”律，即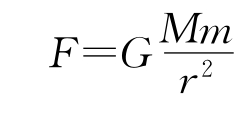

，那么月球轨道上的物体受到的引力比它在地面附近受到的引力要小。

在牛顿时代，重力加速度g、月—地的距离r、月球的公转周期T都能精确地测定，已知r＝3．8×10⁸m，T＝27．3天，g＝9．8m／s²，月球轨道半径即月—地的距离r为地球半径R的60倍，那么——

（1）在月球轨道上的物体受到的引力F ₁是它在地面附近受到的引力F ₂的几分之一？

设物体的质量为m，在月球轨道上的物体受到的引力F ₁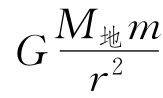＝，物体在地面附近受到的引力则有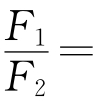

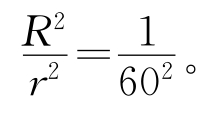
（2）物体在月球轨道上的加速度a（月球公转的向心加速度）是它在地面附近下落的加速度g（重力加速度）的几分之一？

设质量为m的物体在月球的轨道上运动的加速度为a，则a＝r·ω²，ω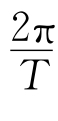＝，r＝60R，得a＝60R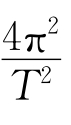，代入数据解得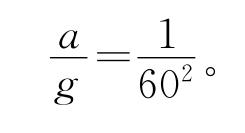由此可见，用数据说明了上述设想的正确性，牛顿的设想经受了事实的检验，地球与月球、地球与地面物体之间的作用力真是同一种力。至此，“平方反比”律已经扩展到太阳与行星之间、地球与月球之间、地球与地面物体之间。

既然太阳与行星之间、地球与月球之间、地球与地面物体之间具有与两个物体的质量成正比、与它们的距离的二次方成反比的引力，那么我们可以更大胆地设想：是否任何两个物体之间都存在这样的力？很可能有，只是因为我们身边的物体质量比天体的质量小得多，我们不易觉察罢了，于是我们可以把这一规律推广到自然界中任意两个物体间，即具有划时代意义的万有引力定律。

阅读教材，理解下面内容：

万有引力是普遍存在于宇宙中任何有质量的物体之间的相互吸引力。日对地、地对月、地对地面上物体的引力都是其实例。

万有引力定律的内容是：自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，引力的大小与物体的质量m₁和m₂的乘积成正比，与它们之间距离r的二次方成反比。可用公式表示：式中力的单位是N，质量的单位是kg，距离的单位是m，G为万有引力常量，G＝6．67×10^－11N·m²／kg²，它在数值上等于质量是1kg的物体相距1m时的相互作用力，单位是N·m²／kg²。

在此，对万有引力定律的表述就是一个具有全称量词的全称命题。

在这节课中，教师通过创设情景，引导学生定量计算，用无可辩驳的事实证明猜想的正确性，增强学生的理性认识，启发学生大胆地猜想，并在教师设问中自主阅读教材，做到有的放矢，最后教师引导学生讨论总结、回答问题，在增强学生的科学表达能力的同时，让学生体会：物理学许多重大理论的发现不是简单的实验总结，它需要直觉和想象力、大胆的猜想和假设，再引入合理的模型，它需要深刻的洞察力、严谨的数学处理和逻辑思想，常常是一个充满曲折和艰辛的过程。上述引导学生发现万有引力定律的思维过程可以概括为：假想—理论推导—实验检验。⁽²⁾

勤思多练

【数学】

指出下列各命题中使用了全称量词的命题。

（1）所有正数都大于负数。

（2）存在一个x∈Z，使2x＋3＝5。

（3）任意三角形中，三角之和是180°。

（4）有的三角形两边之和小于第三边。

（参考提示：“所有”、“任意”都是全称量词。）

【综合】

含有全称量词的命题叫作全称命题，如“对所有的x∈R，x＞3”，“对任意一个x∈Z，2x＋1是整数”等，你能从数学、物理、化学、生物中各举一个全称命题的实例吗？

（参考提示：数学中有“所有的矩形都是平行四边形”；物理中有“声音是由物体振动产生的”；化学中有“化学反应就是物质发生化学变化而产生性质、组成、结构与原来不同的新物质的过程”；生物中有“种子是裸子植物和被子植物特有的繁殖体，它由胚珠经过传粉受精形成，一般由种皮、胚和胚乳三部分组成”。）