图8-12 SMCB工作原理图正常工作时，由于辅助电流回路限流电阻的存在，负载电流主要通过主电流回路；短路开断过程中，其限流性能主要是通过主动触头的快速打开后电流迅速向辅助回路转移，并依靠限流电阻的作用来实现。而当短路发生在SMCB和下级MCB之间时，主回路和辅助回路的双金属片均可能在短延时后动作，从而使机构解锁并实现短路分断。......
2023-06-15
MCB仿真分析：优化与探究
【摘要】：在仿真中，采用动网格技术模拟动触头的运动过程，为了考虑栅片切割电弧后近极压降，模型中在栅片周围包含一层0.1mm厚度的鞘层，鞘层模型采用图8-22所示的非线性电阻。图8-64 MCB灭弧室内温度的分布a）0.05ms b）0.5ms c）3.5ms d）6.5ms图8-65 MCB电弧电压随时间变化的曲线
文献[30]基于三维MHD方法，对真实MCB产品进行了仿真计算，预期短路电流10kA，为了简化计算，缩短计算时间，在计算过程中对模型做了一定的假设和简化处理，假设电弧处于LTE状态，并为层流，铁磁栅片认为是线性的铁磁材料，起弧过程不包括在计算模型中，电弧起始时刻，在动静触头之间有很小的间隙，并设一均匀分布的高温条，从而使电流在动静触头之间流通。在仿真中，采用动网格技术模拟动触头的运动过程，为了考虑栅片切割电弧后近极压降，模型中在栅片周围包含一层0.1mm厚度的鞘层，鞘层模型采用图8-22所示的非线性电阻。
图8-63所示为仿真计算流程图，初始化电弧时，在动静触头之间初始化一个半径为1mm，温度为10000K的圆柱状温度条，然后求解MHD模型中描述流体运动的质量守恒方程、动量守恒方程和能量守恒方程以及描述电磁场的麦克斯韦方程、辐射模型。在求解这些方程的过程中，各参数是相互耦合的，通过求解电位方程可以得到电弧电压值，然后判断电流是否过零，如果电流还未过零，则计算时间增加一个时间步长dt，随后动触头根据设定运动一定的角度，在动触头的这一位置处，继续求解MHD方程，直到电流过零，计算停止。
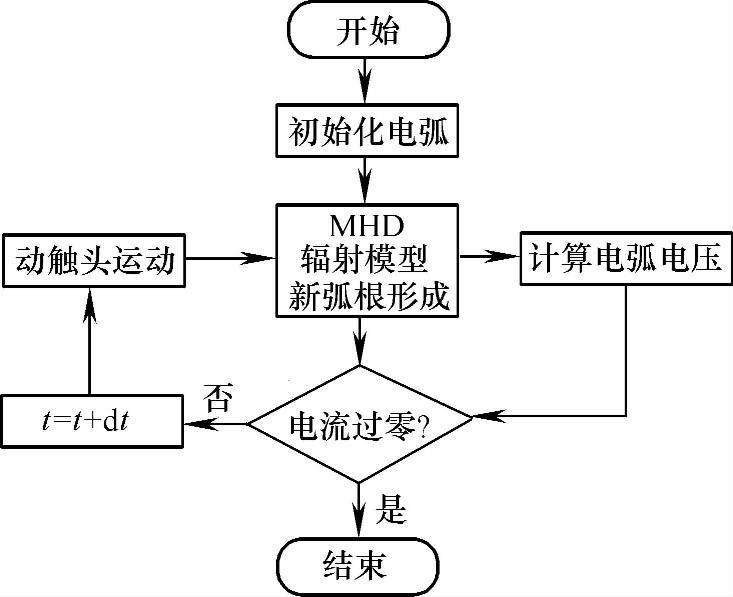
图8-63 计算流程图
图8-64为计算得到不同时刻断路器中温度的分布图像，图8-65为仿真得到的电弧电压和实验得到的电弧电压随时间变化的曲线，由图可以看出，随着动触头的打开，电弧在气吹和洛伦磁力的作用下向栅片运动，电弧电压开始上升，由于电弧还没有进入栅片，故电弧电压较小，在0.5ms时，电弧开始进入栅片，电弧电压进一步升高；在3.5ms时，电弧充满整个栅片区域，被栅片完全切割冷却，电弧电压达到200V左右，随后电弧在栅片中运动，被栅片冷却，电弧温度下降，电流过零前，电弧电压维持在一个较高的数值，从而降低了弧后重燃的可能性。由于MCB中，当电弧电压大于系统电压时，由于限流作用，电弧电流减小，因此最大电流为8kA，小于预期短路电流。此计算模型针对实际断路器产品，虽然计算模型有一定的简化，并未考虑电极和栅片的烧蚀，但也能反映出整个电弧的运动过程，尤其是较好的模拟了电弧被栅片切割成多段短弧的过程，对优化断路器的设计提供了参考。
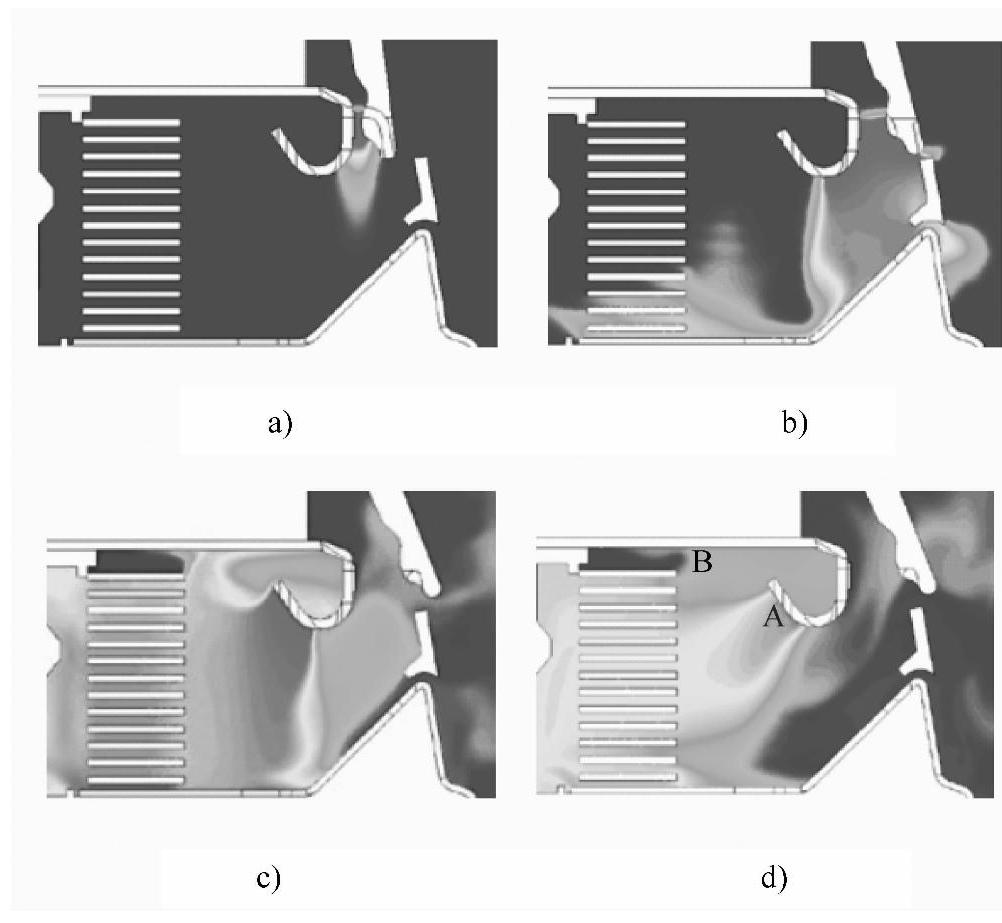
图8-64 MCB灭弧室内温度的分布
a）0.05ms b）0.5ms c）3.5ms d）6.5ms
图8-65 MCB电弧电压随时间变化的曲线
有关低压断路器的建模仿真技术的文章
- 详细阅读
-
仿真设计及性能分析优化方案详细阅读
图9-17未调度任务优先级之和比较图9-18总能耗比较图9-19任务调度完成时刻比较由图9-17、图9-18、图9-19可知，在选取的6个仿真场景中，MNSGA-Ⅱ对于目标函数f 1，f 2和f 3的优化效果均优于MOGA，其中未调度任务优先级权值之和的平均值降低了66.77%，总能耗平均值降低了69.73%，任务调度完成用时平均值降低了35.27%。......
2023-07-02
-
MCCB仿真分析：探究电路保护器的性能详细阅读
由以上仿真结果和实验结果对比可以看出，用MHD仿真MCCB的模型中，动触头的运动过程对电弧电压以及电弧能量的准确性影响非常重要，同时，通过实验验证了在仿真中采用ANSYS Emag软件计算电磁场，用FLUENT计算流场的耦合方法的有效性和准确性，因此在低压断路器的仿真中，为了得到更为准确的计算结果，动触头的运动过程必须在仿真模型中予以考虑。......
2023-06-15
- 详细阅读
-
轴销寿命分析：优化方法探究详细阅读
图3-16 轴销寿命分布云图a）A3钢 b）调质45钢 c）调质40Cr由图3-16可见：1）轴销中间凸台部分的两侧寿命较短，是其薄弱环节，该结果与ADAMS软件的应力应变计算结果相符。2）轴销14698号节点的疲劳寿命最短，当选用材料为A3钢时，其疲劳寿命仅有4020次；当选用材料为调质45钢时，其疲劳寿命约为14000次，相比预期10000次机械寿命裕量较小；当选用材料为调质40Cr时，其疲劳寿命约为23000次，可以满足机械寿命10000次的要求，但是需要较高的材料成本。......
2023-06-15
-
镍氢电池仿真模型探究详细阅读
表8.5充放电状态实验数据由于开路电压VOC与电池参数SOC的关系高度非线性，因此我们采用高阶多项式函数进行拟合。图8.22镍氢电池仿真模型在实际情况下，电池也会受到温度的影响，有一种映射关联。图8.23SOC计算模块参数更新模块根据当前的电池值计算相应的开路电压值，同时考虑在前述的多项式拟合方法中获得的充放电过程之间的函数关系。......
2023-06-23
-
电磁暂态仿真模型分析的优化方法详细阅读
第二部分是将每个IMF信号进行希尔伯特变换，从而得到信号的希尔伯特谱。Prony算法不仅可以对仿真结果进行分析，还能够对现场的实时测量数据进行分析，具有很高的工程实用性。......
2023-06-25
-
仿真实验及结果分析优化方案详细阅读
图9-34比较了在不同任务规模下两种算法优化结果中的续传次数，MACA算法中的续传次数要低于NSGA-Ⅱ算法，平均减少了25.1%。图9-35是两种算法优化结果的资源负载失衡度，MACA算法与NSGA-Ⅱ算法结果相当，两算法的负载失衡度均在0.01以下。对本章场景仿真实验，分别得到整传调度和续传调度结果如图9-36和图9-37所示。......
2023-07-02
相关推荐