电弧等离子体的基本物性参数

2023-06-15 百科知识版权反馈

【摘要】：计算断路器电弧等离子体的化学组成，不仅是计算电弧属性必要的第一步，也是认识等离子化学过程的重要一环。图8-26为空气电弧等离子体平衡态下的化学组成，其中n为粒子数密度，T为温度。图8-27 断路器电弧中等离子体半径对净发射系数的影响P1模型最早应用于燃烧系统的数值模拟中。

要研究空气电弧的磁流体动力学数学模型，首先必须掌握电弧的基本物性参数，包括：电弧等离子体平衡态化学组成、热动属性及传输参数；辐射特性及辐射数学模型等。

断路器电弧的基本特征是：电场强度相当低（低于数kV/m），但电子和离子数密度非常高（大于10²³m^-3）；一般满足局部热动平衡（Local Thermodynamic Equilibrium，LTE）条件，且温度一般为10000K量级，也就是1eV数量级，最高可达25000K。

一般来说，局部热动平衡必须满足以下4个条件^[33]：

1）等离子体中所有粒子的速度分布函数满足麦克斯韦分布；

2）等离子体中所有处于激发态的粒子数密度满足玻尔兹曼分布；

3）等离子体中所有粒子的浓度可以在化学平衡的条件下计算；

4）分别对应于以上3个条件的运动温度、激发温度和反应温度必须相等。

LTE状态下，等离子体的局部化学组成仅仅取决于局部温度，压力和化学要素的浓度，通常基于质量守恒法则可求得平衡态化学组成。计算断路器电弧等离子体的化学组成，不仅是计算电弧属性必要的第一步，也是认识等离子化学过程的重要一环。计算温度从等离子体的边缘温度，即接近室温，到中心区域约30000K以上。在这个温度范围内，根据不同的化学反应，需要考虑很多不同的物质种类。在空气电弧中，N2、N₂⁺、N、O、O⁺和电子等占重要的浓度。图8-26为空气电弧等离子体平衡态下的化学组成，其中n为粒子数密度，T为温度。

一旦等离子的化学组成确定后，利用各种粒子的质量、焓和数密度等数据，就可以计算出其热动属性，即焓、比热和密度参数。而求解描述电子能量分布的波尔兹曼方程，可得到等离子体的扩散系数、粘度、热导率和电导率等传输参数。

图8-26 空气（78.86%的氮气，21.14%氧气）等离子体的平衡态化学组成

辐射是热等离子体中的一个重要现象和研究内容，尤其是对于开关电弧来说，辐射是能量传递最主要的方式。一般来说，辐射的影响表现在以下3个方面：1）在温度最高的区域，辐射常常是最重要的能量耗散方式；2）辐射热传递是等离子体内部的一种有效能量交换方式；3）等离子体辐射出的能量可以加热周围的气体或者侵蚀外部材料。

在LTE条件下，式（8-29）所示的基尔霍夫（Kirchhoff）公式描述了热等离子中的辐射规律^[33]。其中ε_v和K_v分别为发射和吸收系数，B_v表示普朗克函数，ν为频率，h为普朗克常数，c为光速，T为温度。

尽管式（8-29）所示的关系比较简单，但是在热等离子体的辐射建模中，需要大规模的迭代运算，因此要严格计算等离子体的辐射是非常困难的。这是因为：一方面需要在整个光谱范围内对每一个单元的发射和吸收进行计算；另一方面光谱是由连续光谱和线光谱组成，而谱线取决于等离子体中的离子能量水平。此外，压力和温度对辐射有直接的影响。

下面简要介绍了几种目前常用的辐射数学模型，包括净发射系数模型（Net Emission Co-efficient，NEC），P1模型，局部特性法（Method of Partial Characteristics，MPC），灰体辐射模型，离散坐标法（Discrete Ordinate，DO）等。

净发射是指一个等温球中发射和吸收能量之间的差值。式（8-30）给出了净发射系数ε_N的表达式，其中R_P为球半径。图8-27为断路器电弧中不同等离子体半径R_P时净发射系数ε_N随温度的变化规律^[16]。可以看出，随着R_P的减小，ε_N的数值越大。当R_P=0时，也就是对应于光学薄层等离子体，大约有90%的辐射能量被发射点1mm内的等离子体吸收。

值得指出的是，很多学者对NEC方法进行了深入的研究，并得到了很有价值的数据，他们已经将ε_N与温度、压力和平均等离子半径的关系做成了表格，以便于对等离子体的进一步研究。然而，从本质上讲，NEC方法可以比较理想地分析电弧中心区域的温度分布，而对温度较低的电弧边缘区域并不能得到较好的结果。

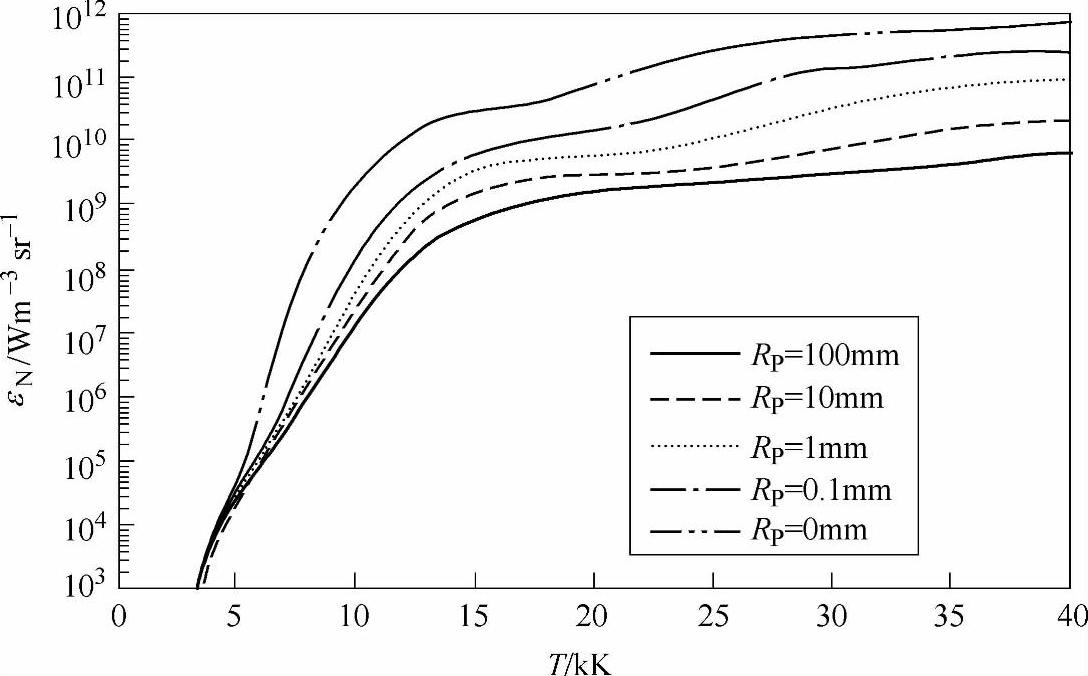
图8-27 断路器电弧中等离子体半径对净发射系数的影响

P1模型最早应用于燃烧系统的数值模拟中。和NEC模型相比较，P1模型更适合于考虑等离子体边缘区域和器壁对辐射的影响。P1模型的一个基本假定就是：在一个给定的温度下，平均吸收系数在频域内是一个常数。该方法基本原理是基于求解式（8-31）所示的辐射热传导方程，其中I_v为∧s方向上的光谱辐射强度，K_v和σ_sv分别为光谱吸收和散射系数，I_bv为黑体辐射强度，φ_v为光谱散射强度函数，Ω_v为空间角^[33]。

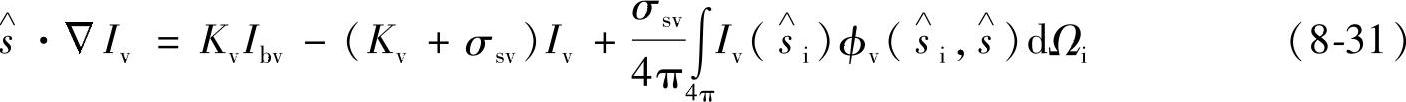
在P1模型中，辐射强度可由式（8-32）来表示，其中G_v为入射辐射，q_v为辐射通量。对开关电弧来说，可以忽略式（8-31）中的散射项，这样将式（8-32）带入式（8-31），然后对整个空间角进行积分运算，就可以得到式（8-33）所示的P1模型控制方程。

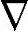G_v=-3K_vq_v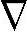，·q_v=K_v（4πI_bv-G_v）（8-33）

MPC方法早在1979年时被Sevast’yanenko提出，但一直到近10年才应用到电弧等离子体的研究中，其主要的优点是可以更为精确地考虑电弧边缘较冷的区域对电弧中心区域辐射的吸收作用^[34]。MPC方法的最基本原理是认为辐射的源点X和辐射路径上的任意点_η之间的温度变化总是线性的，以源点温度T_X，积分路径上的任一点温度T_η，η和两点之间的距离|X-η|为变量，可以计算出式（8-34）和（8-35）所示局部特性函数的Som和ΔSim随这些量变化的数据表格，然后采用插值的方法就可以求得任意组合的T_X、T_η、η和|X-η|时对应的函数值，其中Y表示等离子体的边缘。局部特征函数与两点的温度及间距有关，因此MPC方法能够考虑边缘区域对于能量辐射的自吸收。而且在等离子体建模时，可以与流场解耦而提前计算出辐射参数，这也是MPC方法的最大特点。

这样，根据辐射热传递方程，辐射通量的散度可以用式（8-36）来表示。在进行热等离子体建模时，就可以将该式带入能量守恒方程进行求解。

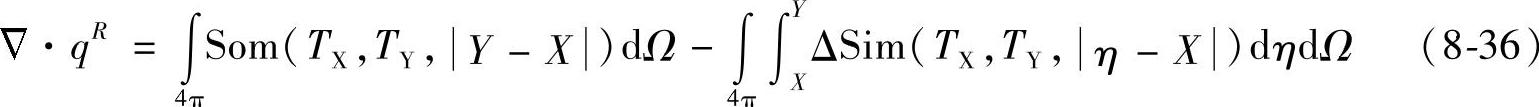
此外，Lindmayer也提出了断路器电弧的灰体辐射模型[15]。该模型认为每一个控制体积均是一个独立的辐射发射源，并给出了单位体积发射功率S_R的表达式，如式（8-37）所示，其中T₀为环境温度。这样，将式（8-37）带入能量守恒方程，就可以考虑辐射对电弧运动和特性的影响。

S_R=4αk（T⁴-T⁴₀），其中

DO法是一种基于坐标离散的方法，将辐射密度在不同的方向进行离散分解，设将其分解在n个不同的方向上，则方程如下：

以上方程在每一个波带都需要求解，设有i个波带，则能量方程中的辐射源项如下：

其中，ω_j为在方向上的正交权重。

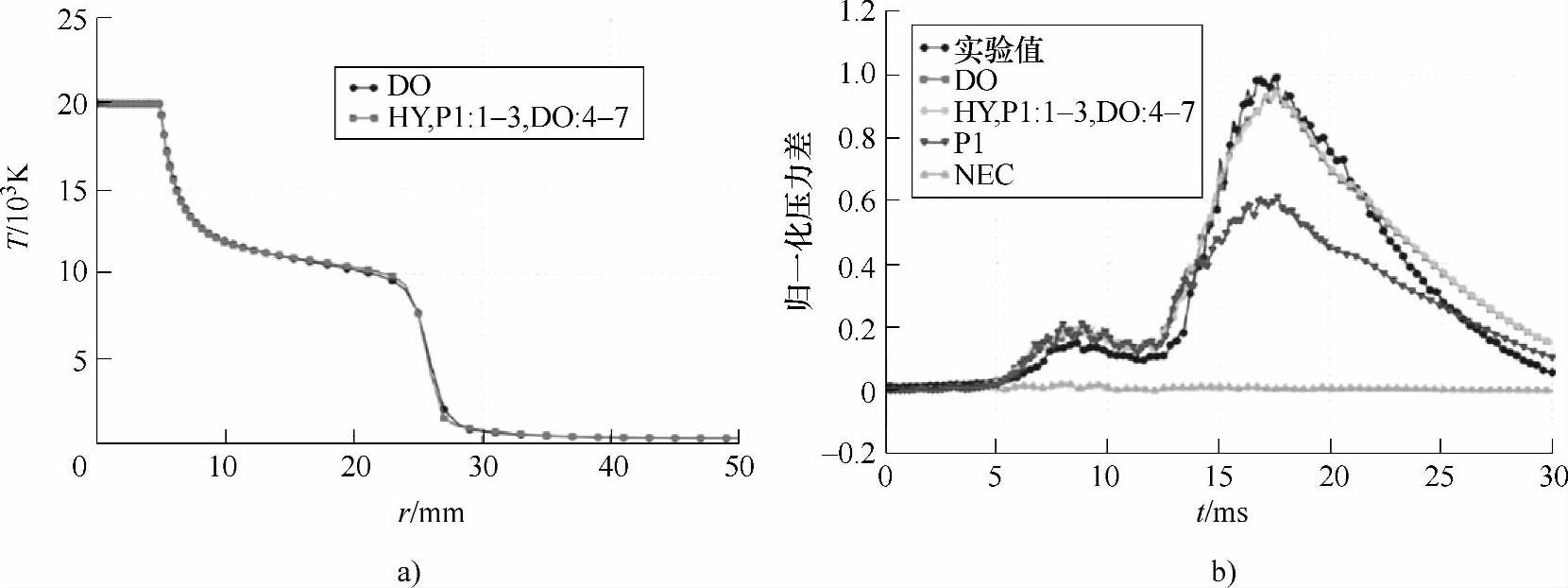
图8-28 不同辐射计算方法的结果对比

a）温度随半径的变化曲线 b）压力差对比

以上几种辐射计算模型中，灰体辐射模型简单易实现，NEC方法由于没有考虑低温区域的重吸收，计算结果不是十分准确，P1模型考虑了低温区的重吸收，因此计算结果相较NEC准确。但是P1模型在光学厚度薄层时，计算受到限制；DO模型计算辐射最为准确，但是计算复杂，花费时间很长；针对此，文献^[35]提出了辐射的混合计算方法，即采用P1+DO的模型，在1-3条谱线时使用P1模型，4-7条谱线使用DO模型。计算结果如图8-28所示。由图可以看出，HY混合辐射模型的计算结果和DO模型计算的结果吻合的很好，由图8-28可以看出HY和DO辐射模型的计算结果更接近于实验结果，但HY相比DO模型耗时较少，因此HY的方法兼顾了准确性和耗时两方面，是仿真中较好的选择。

电弧等离子体的基本物性参数

相关推荐