图8-3为额定电流为16A的微型断路器，当短路电流通过瞬动电磁铁线圈时，铁心向左移动，顶动脱扣杆，使机构脱扣。图8-3 微型断路器现对上述微型断路器描述其仿真过程。为了验证计算准确性，在预期电流Ip=10.2kA，U=232V，cosφ=0°，βv=4.5257×10-7条件下进行了开断试验，试验结果与计算机仿真进行了对比，如图8-7所示。......
2025-09-29
SMCB开断过程仿真及实验结果：额定电流35A优化研究
【摘要】：2.预期短路电流Ie=1.5kA图8-18a、图8-18b、图8-18c分别为实验回路额定电压U=230V，预期短路电流有效值Ie=1.5kA、合闸相角ψ=0°时的SMCB两端电压、流过主回路和辅助回路的电流、回路总电流的计算结果，在主回路电流励磁作用下气隙1和作用在MR-35磁脱扣器动铁心上的电磁力计算结果，开断过程中系统电压、短路电流和SMCB两端电压的实验结果。
1.预期短路电流Ie=644A
图8-15a和图8-15b分别为额定电流35A的SMCB（配MR-35磁脱扣器）在预期短路电流Ie=644A、ψ=0°时短路电流和SMCB两端电压的仿真和实验结果。
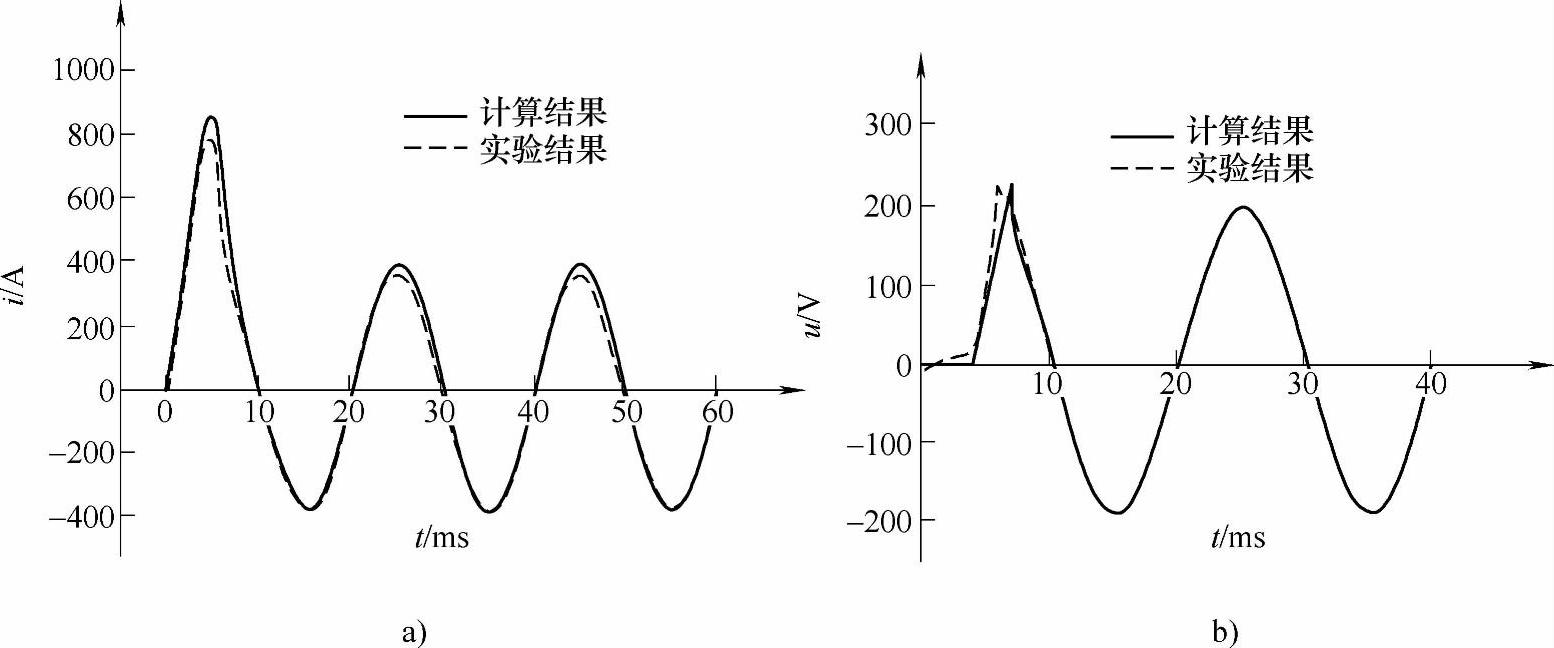
图8-15 Ie=644A、ψ=0°时短路电流和SMCB两端电压的计算和实验结果
a）短路电流计算和实验结果对比 b）SMCB两端的电压计算和实验结果对比
表8-1对比了开断过程的典型参数计算和实验结果，其中tip为短路电流到达峰值的时间，up为电压的峰值，tup为电弧电压到达峰值的时间。可以看出，计算和实验结果值较为接近，这也在一定程度上验证了上述开断过程仿真方法的正确性。
表8-1 典型开断参数的计算和结果对比（Ie=644A和ψ=0°）
图8-16a、图8-16b、图8-16c分别为实验回路额定电压U=230V，预期短路电流有效值Ie=644A、合闸相角ψ=45°时的SMCB两端电压、流过主回路和辅助回路的电流、回路总电流的计算结果，在主回路电流励磁作用下气隙1和作用在MR-35磁脱扣器动铁心上的电磁力计算结果，开断过程中系统电压、短路电流和SMCB两端电压的实验结果。
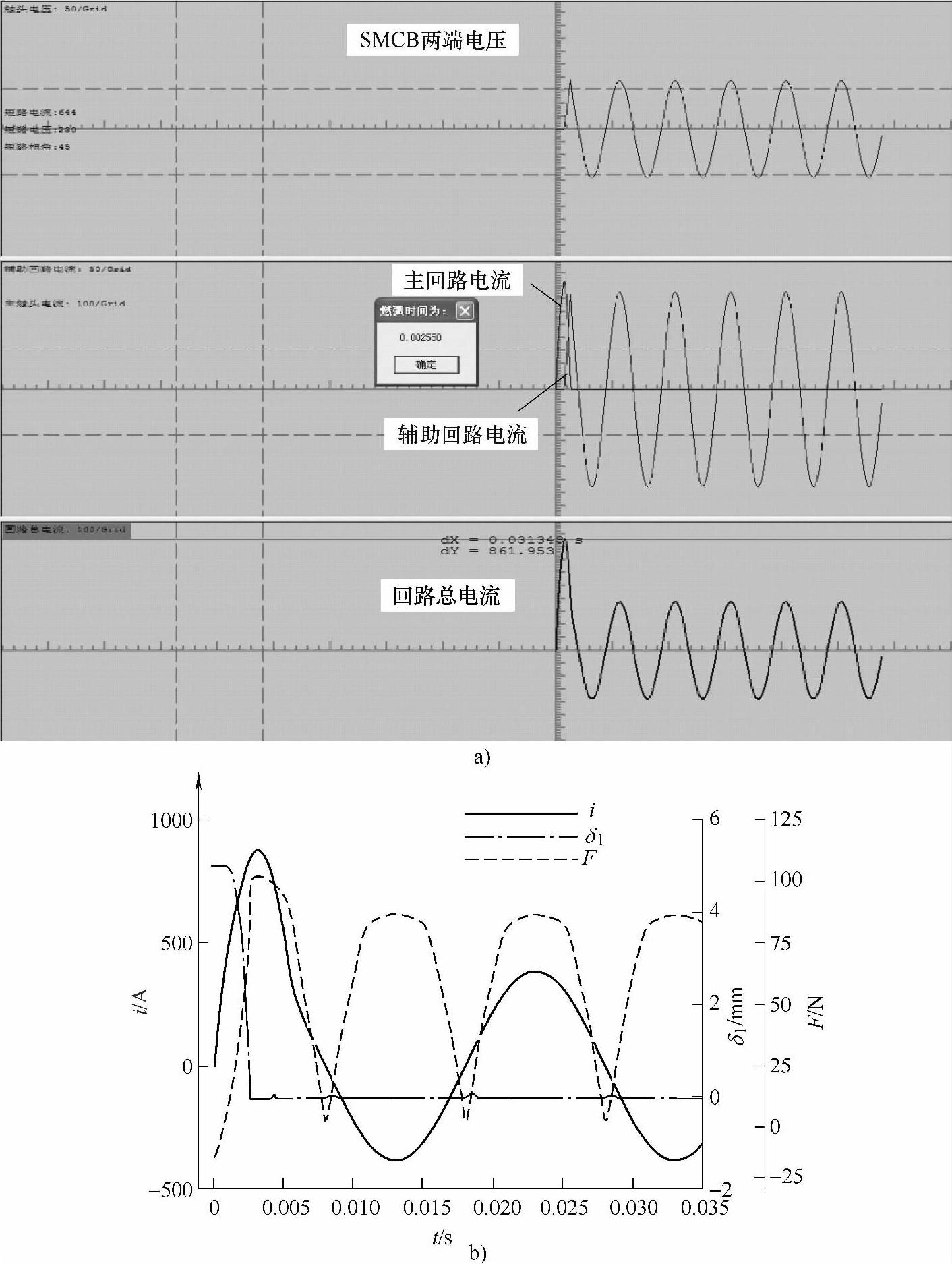
图8-16 预期短路电流有效值为644A、合闸相角为45°的开断过程仿真和实验结果
a）SMCB两端电压、主回路电流、辅助回路电流和回路总电流的计算结果 b）短路电流、气隙1、作用在动铁心上的电磁力随时间变化的计算结果
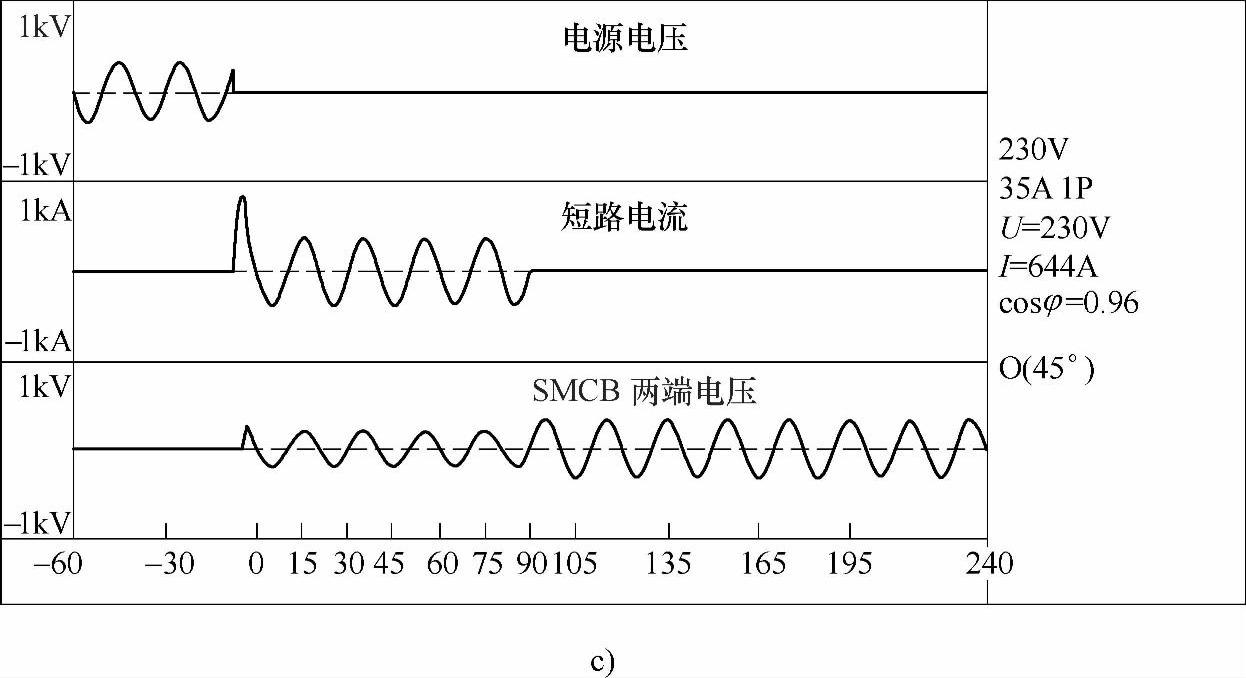
图8-16 预期短路电流有效值为644A、合闸相角为45°的开断过程仿真和实验结果（续）
c）短路开断过程的实验结果
图8-17a、图8-17b、图8-17c分别为实验回路额定电压U=230V，预期短路电流有效值Ie=644A、合闸相角ψ=90°时的SMCB两端电压、流过主回路和辅助回路的电流、回路总电流的计算结果，在主回路电流励磁作用下气隙1和作用在MR-35磁脱扣器动铁心上的电磁力计算结果，开断过程中系统电压、短路电流和SMCB两端电压的实验结果。
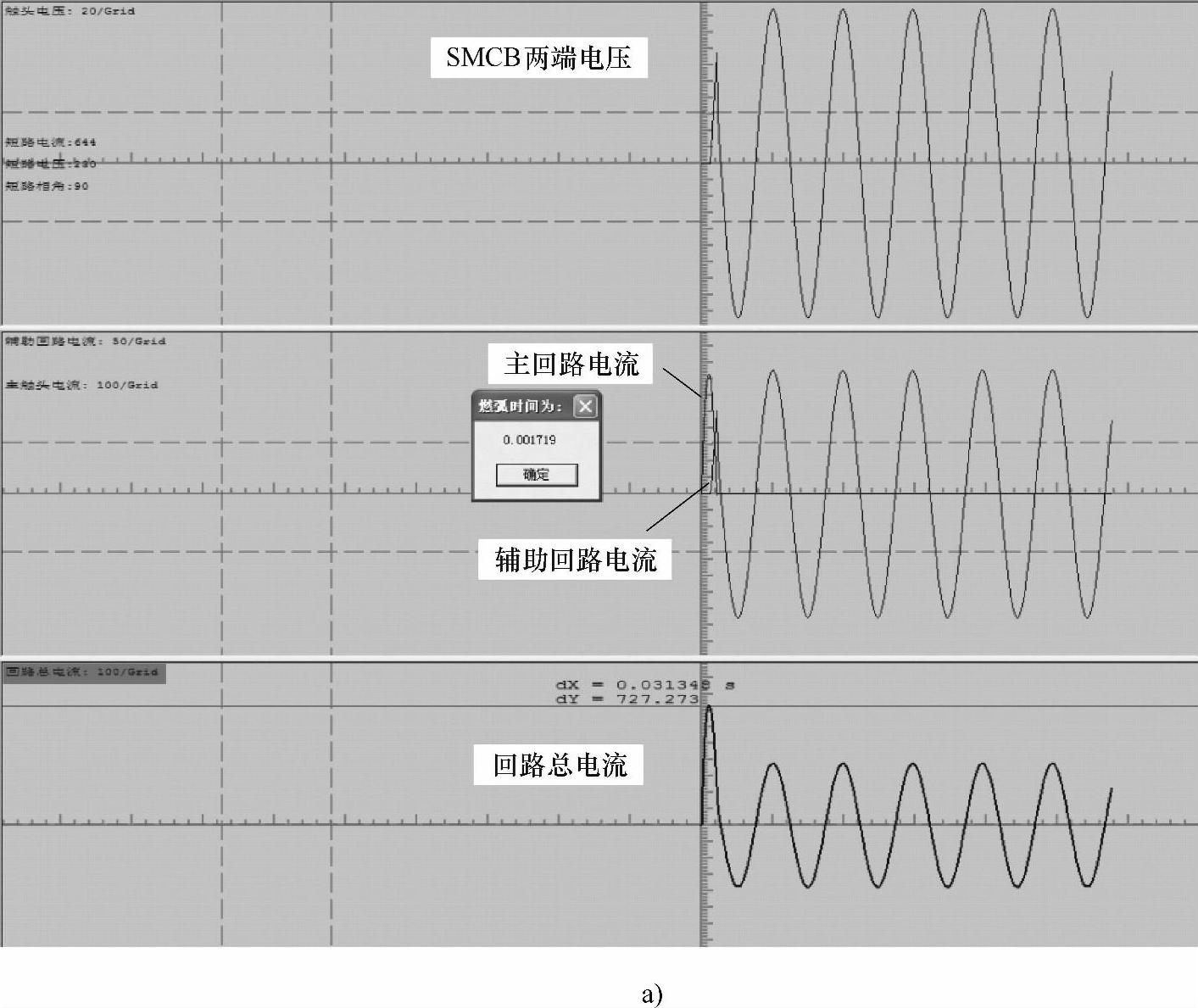
图8-17 预期短路电流有效值为644A、合闸相角为90°的开断过程仿真和实验的结果
a）SMCB两端电压、主回路电流、辅助回路电流和回路总电流的计算结果
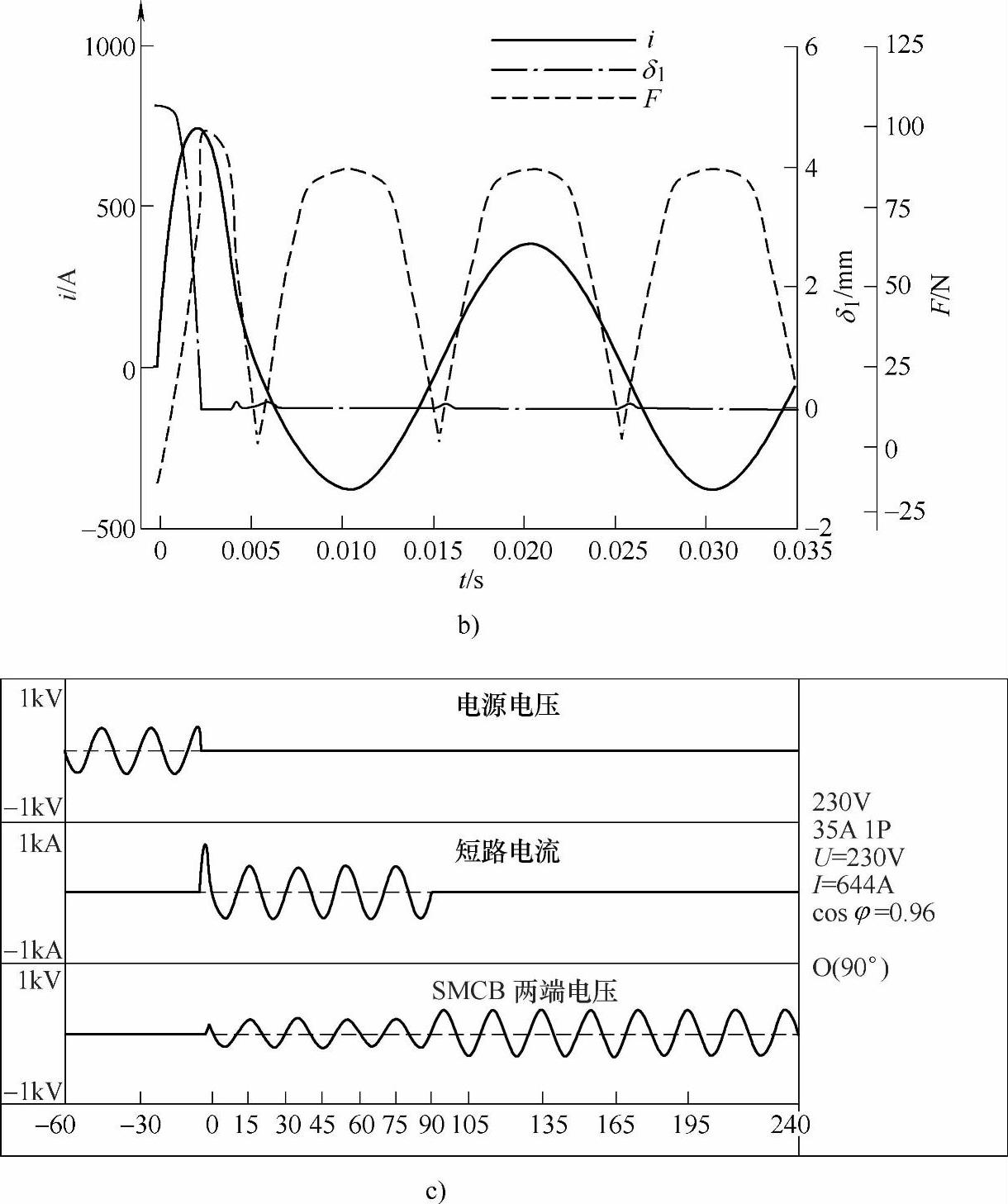
图8-17 预期短路电流有效值为644A、合闸相角为90°的开断过程仿真和实验的结果（续）
b）短路电流、气隙1、作用在动铁心上的电磁力随时间变化的计算结果 c）短路开断过程的实验结果
表8-2对比上述SMCB开断过程的部分典型参数的计算和实验结果。可以看出，计算结果和实验结果值比较符合。(https://www.chuimin.cn)
表8-2 典型开断参数的计算和结果对比（Ie=644A，ψ=45°和90°）
同时，结合表8-1所示的结果，可以看出：随着合闸相角的增大，主动、静触头开始分离的时间ti逐渐减小，这主要是由于短路电流上升更快、作用在脱扣器动铁心上电磁力也相应地增长较快；同时燃弧时间也越来越短，相应地电弧电压也越来越低。
2.预期短路电流Ie=1.5kA
图8-18a、图8-18b、图8-18c分别为实验回路额定电压U=230V，预期短路电流有效值Ie=1.5kA、合闸相角ψ=0°时的SMCB两端电压、流过主回路和辅助回路的电流、回路总电流的计算结果，在主回路电流励磁作用下气隙1和作用在MR-35磁脱扣器动铁心上的电磁力计算结果，开断过程中系统电压、短路电流和SMCB两端电压的实验结果。
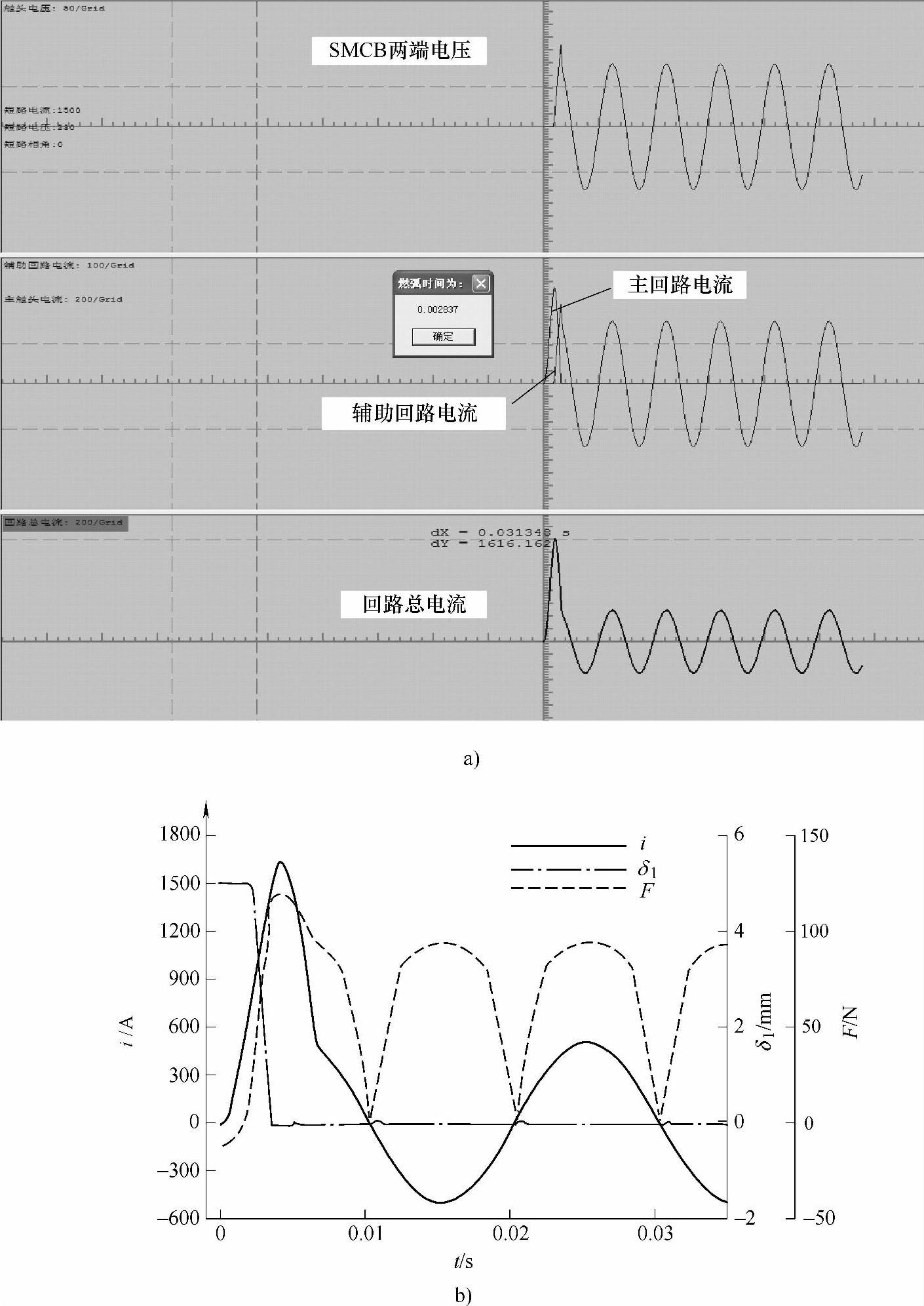
图8-18 预期短路电流有效值为1.5kA、合闸相角为0°的开断过程仿真和实验的结果
a）SMCB两端电压、主回路电流、辅助回路电流和回路总电流的计算结果 b）短路电流、气隙1、作用在动铁心上的电磁力随时间变化的计算结果
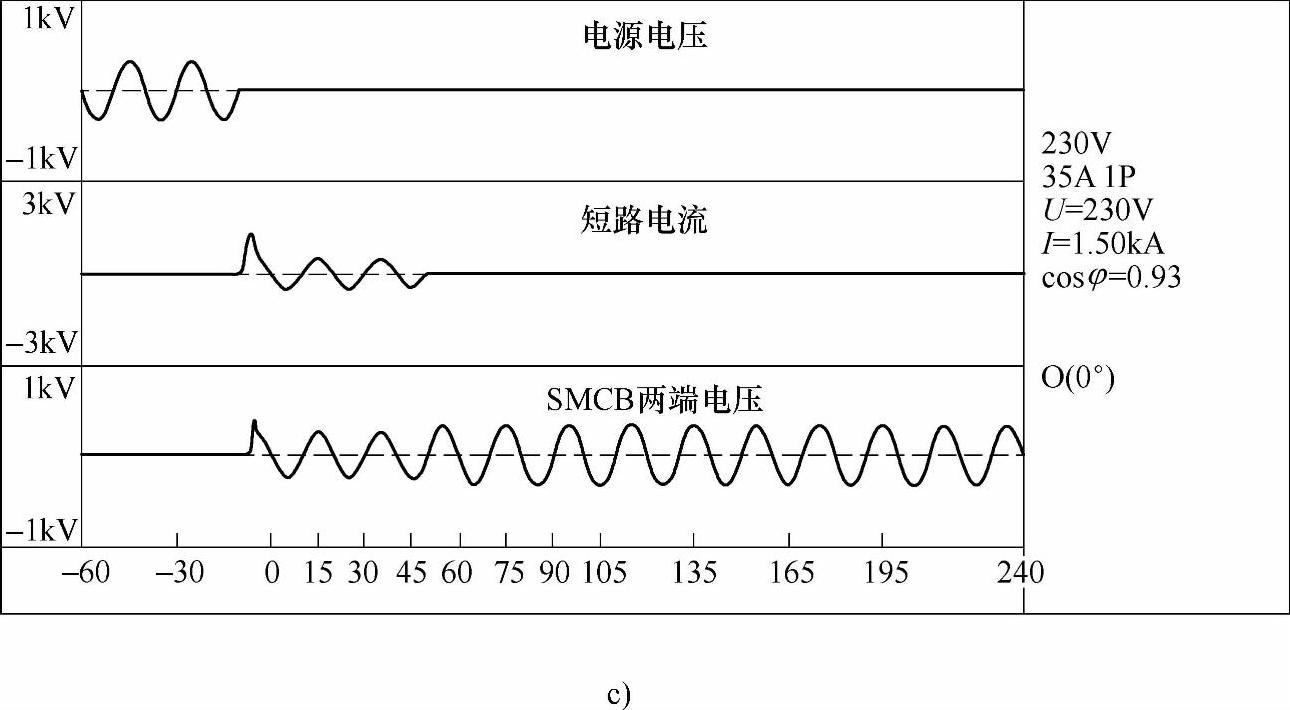
图8-18 预期短路电流有效值为1.5kA、合闸相角为0°的开断过程仿真和实验的结果（续）
c）短路开断过程的实验结果
图8-19a、图8-19b、图8-19c分别为实验回路额定电压U=230V，预期短路电流有效值Ie=1.5kA、合闸相角ψ=90°时的SMCB两端电压、流过主回路和辅助回路的电流、回路总电流的计算结果，在主回路电流励磁作用下气隙1和作用在MR-35磁脱扣器动铁心上的电磁力计算结果，开断过程中系统电压、短路电流和SMCB两端电压的实验结果。
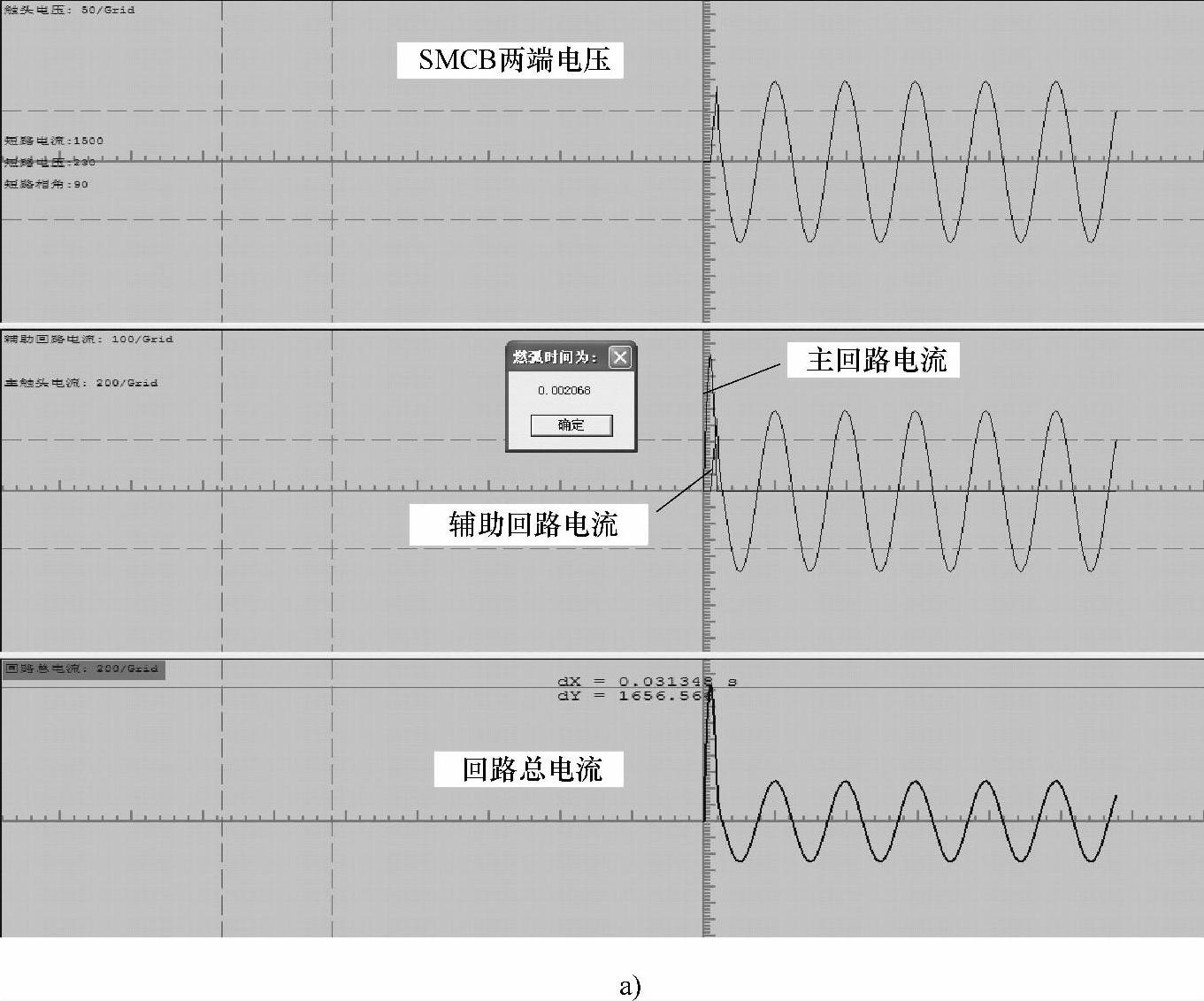
图8-19 预期短路电流有效值为1.5kA、合闸相角为90°的开断过程仿真和实验结果
a）SMCB两端电压、主回路电流、辅助回路电流和回路总电流的计算结果
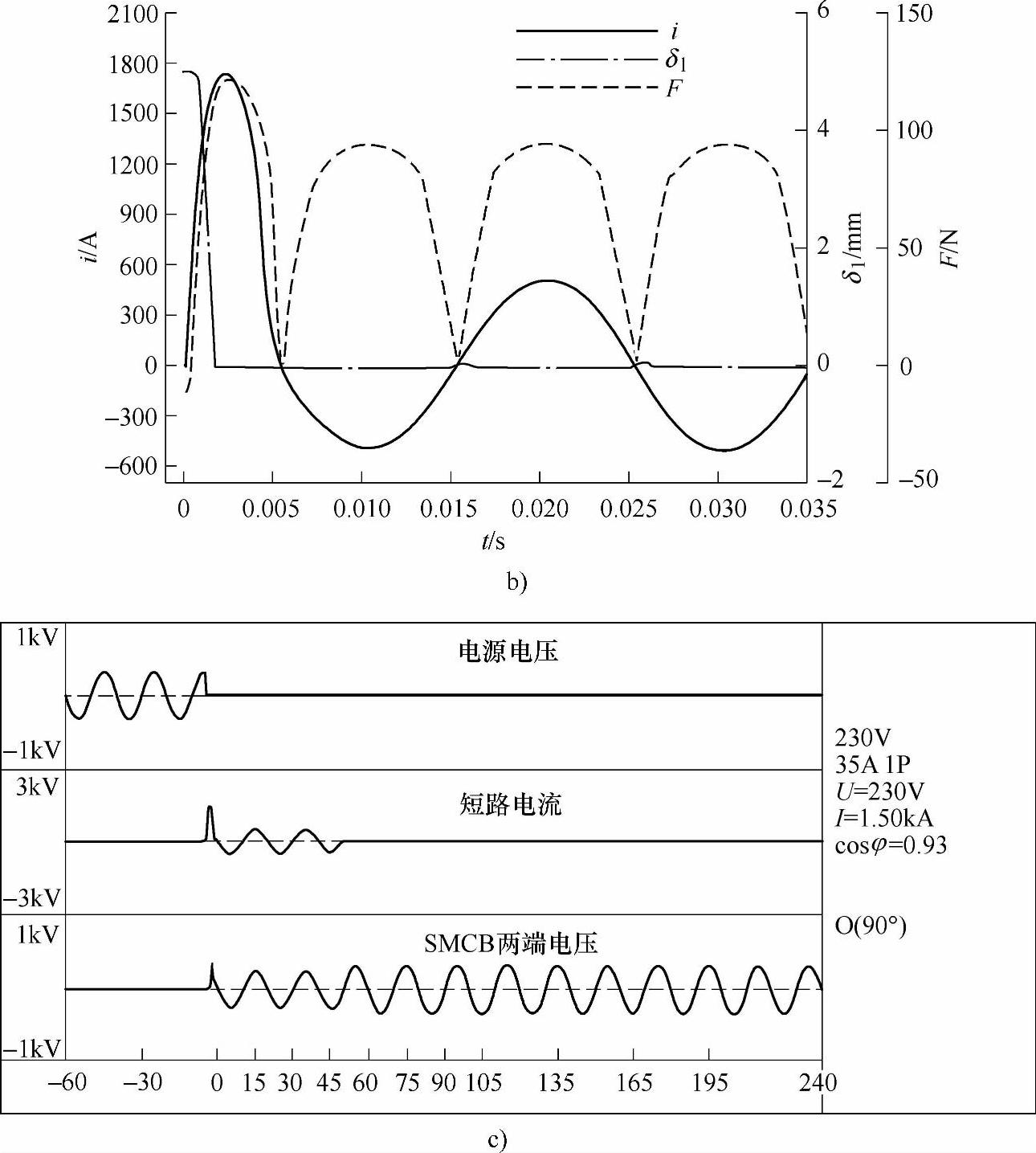
图8-19 预期短路电流有效值为1.5kA、合闸相角为90°的开断过程仿真和实验结果（续）
b）短路电流、气隙1、作用在动铁心上的电磁力随时间变化的计算结果 c）短路开断过程的实验结果
表8-3对比上述1.5kA短路电流时的SMCB开断过程的部分典型参数的计算和实验结果。可以看出，计算结果和实验结果值也较为接近。同样地，随着合闸相角的增大，主动静触头开始分离的时间ti和燃弧时间ta越来越短。
表8-3 典型开断参数的计算和结果对比（Ie=1.5kA，ψ=0°和90°）
相关文章
- 详细阅读
-
电弧产生的气动斥力研究及实验结果探讨详细阅读
一旦电动斥力的数值超过触头预压力，动触头即斥开并在触头间产生电弧。此后，Holm力即消失，然而与此同时，由于电弧与电极、器壁等之间的相互作用，会在动触头上作用另外一个力，称之为气动斥力FB，其方向和动触头的运动方向相同。FB=Δp×Ac Shea[6-1]和Zhou[6-2]结合实验，从理论上给出了气动斥力的分析和计算方法。以下主要介绍气动斥力的实验研究结果。......
2025-09-29
-
实验方法及结果分析详细阅读
实验中触头预压力FK保持为25.1N。表6-5为两组实验和仿真的详细结果数据。图6-21为峰值电流为11.3kA时的电流和电动斥力实验波形。表6-5 实验和仿真结果比较在仿真中，表征触头接触情况的参数ξ取值为0.45。而电流峰值为9.0和11.3kA时，对应的触头压力分别为35.4和55.9N。根据式（6-1），可得导电斑点的半径分别为0.158和0.199mm。因此，引入导电桥模型，采用有限元静态分析的方法计算电动斥力是合理的，也是有效的。......
2025-09-29
-
如何计算SMCB开断过程的电参数？详细阅读
通过求解上述方程、和，就可以获得SMCB开断过程的电参数，图8-14给出了相应的计算流程图。图8-14 SMCB开断过程的计算方法要获得ti值时需要进行开断过程仿真，首先要计算出磁脱扣器的静态特性，即作用在动铁心上的电磁力与气隙和电流之间的关系数据，然后基于多体动力学软件ADAMS，并进行二次开发，实现电磁-机械过程的耦合仿真，建立开断过程的动力学模型，得到主动、静触头的分离时刻ti和电流I1。......
2025-09-29
-
低压配电柜温升特性的仿真及实验研究详细阅读
图5-25 纵截面气体流速分布图2.实验验证为了验证仿真模型，分别完成了开关柜额定电流为630A的温升实验和降容运行条件下500A的温升实验，接线图如图5-26a所示。......
2025-09-29
-
分断短路电流实验研究：优化方案详细阅读
实验中的故障电流是利用单频振荡回路提供的，主要是将大型电容器组充电后使之对电感放电以产生工频电流。实验开始前，S1打开，通过整流器对电容器组Ci充电，当达到实验所需的电压后，断开充电电路，即可开始实验。图2-14 实验电路图图2-15是预期电流10kA时对断路器进行实测的短路试验波形，图中通道CH1、通道CH2和通道CH3分别为短路电流、电弧电压和主轴转角。根据实验条件，以下仅分析单相短路情况，并认为短路电流作用在中相触头系统。......
2025-09-29
- 详细阅读
-
实验模型及方法详解详细阅读
实验采用对称的双断口结构，图6-25所示为实验模型的平面图及相关几何尺寸，单位均为mm。图6-25 气动斥力实验模型的平面图图6-26 气动斥力测试方法的原理图测量方法的原理如图6-26所示。下面的实验均是采用该方法进行的。图6-29 s=2mm，Im=4.2kA时的实验波形及电动斥力、气动斥力随时间的......
2025-09-29
相关推荐